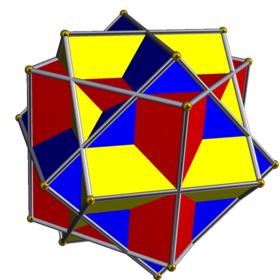
Compound of three cubes

Compound of three cubes
Type	Uniform compound
Index	UC8
Convex hull	Nonuniform truncated octahedron
Polyhedra	3 cubes
Faces	6+12 squares
Edges	36
Vertices	24
Symmetry group	octahedral (Oh)
Subgroup restricting to one constituent	4-fold prismatic (D4h)

This uniform polyhedron compound is a symmetric arrangement of 3 cubes, considered as square prisms. It can be constructed by superimposing three identical cubes, and then rotating each by 45 degrees about a separate axis (that passes through the centres of two opposite faces).

This compound appears in the lithograph print Waterfall by M.C. Escher. Its dual, the compound of three octahedra, forms the central image in an earlier Escher woodcut, Stars.

Cartesian coordinates

Cartesian coordinates for the vertices of this compound are all the permutations of

(±√2, 0, ±1)

Related compounds

If the cubes are compressed into rhombic prisms, a compound of 3 rhombic prisms is constructed. The compound has pyritohedral symmetry.

Its vertices are parametrized with lengths a and b with values besides √2.

(±a,  0, ±1), ( 0, ±b, ±1)

(±b, ±1,  0), ( 0, ±1, ±a)

(±1, ±a,  0), (±1,  0, ±b)

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554.