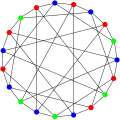
Robertson graph
| Robertson graph | |
|---|---|
 The Robertson graph is Hamiltonian. | |
| Named after | Neil Robertson |
| Vertices | 19 |
| Edges | 38 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 5 |
| Automorphisms | 24 (D12) |
| Chromatic number | 3 |
| Chromatic index | 5[1] |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Cage Hamiltonian |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.[2][3]
The Robertson graph is the unique (4,5)-cage graph and was discovered by Robertson in 1964.[4] As a cage graph, it is the smallest 4-regular graph with girth 5.
It has chromatic number 3, chromatic index 5, diameter 3, radius 3 and is both 4-vertex-connected and 4-edge-connected. It has book thickness 3 and queue number 2.[5]
The Robertson graph is also a Hamiltonian graph which possesses 5,376 distinct directed Hamiltonian cycles.
Algebraic properties
The Robertson graph is not a vertex-transitive graph and its full automorphism group is isomorphic to the dihedral group of order 24, the group of symmetries of a regular dodecagon, including both rotations and reflections.[6]
The characteristic polynomial of the Robertson graph is
Gallery
-
The Robertson graph as drawn in the original publication.
-
The chromatic number of the Robertson graph is 3.
-
The chromatic index of the Robertson graph is 5.
References
- ^ Weisstein, Eric W. "Class 2 Graph". MathWorld.
- ^ Weisstein, Eric W. "Robertson Graph". MathWorld.
- ^ Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.
- ^ Robertson, N. "The Smallest Graph of Girth 5 and Valency 4." Bull. Amer. Math. Soc. 70, 824-825, 1964.
- ^ Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- ^ Geoffrey Exoo & Robert Jajcay, Dynamic cage survey, Electr. J. Combin. 15, 2008.