Bilunabirotunda

Bilunabirotunda
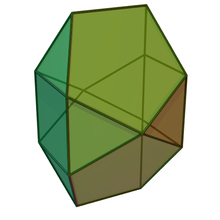Type	Johnson J90 - J91 - J92
Faces	2x4 triangles 2 squares 4 pentagons
Edges	26
Vertices	14
Vertex configuration	4(3.52) 8(3.4.3.5) 2(3.5.3.5)
Symmetry group	D2h
Dual polyhedron	-
Properties	convex
Net

In geometry, the bilunabirotunda is one of the Johnson solids (J₉₁). It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids.

A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.

Cartesian coordinates

The following define the vertices of a bilunabirotunda centered at the origin with edge length 1:

$\left(0,0,\pm {\frac {\varphi }{2}}\right)$

$\left(\pm {\frac {(\varphi +1)}{2}},\pm {\frac {1}{2}},0\right)$

$\left(\pm {\frac {1}{2}},\pm {\frac {\varphi }{2}},\pm {\frac {1}{2}}\right)$

where $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ is the golden ratio.

Related polyhedra and honeycombs

Further information: Dodecahedron § Space_filling_with_cube_and_bilunabirotunda

Six bilunabirotundae can be augmented around a cube with pyritohedral symmetry. B. M. Stewart labeled this 6 bilunabirotundae model as 6J₉₁(P4).

The bilunabirotunda can be used with the regular dodecahedron and cube as a space-filling honeycomb.

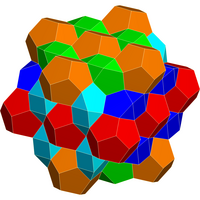Spacefilling honeycomb

6 bilunabirotundae around a cube

External links

• Weisstein, Eric W., "Bilunabirotunda" ("Johnson solid") at MathWorld.
• Miracle Spacefilling (Dodecahedron&Cube&Johnson solid No.91)