Citation graph
This article may be in need of reorganization to comply with Wikipedia's layout guidelines. (January 2021) |
| Part of a series on |
| Citation metrics |
|---|
 |
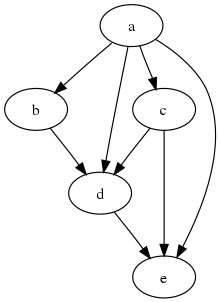
A citation graph (or citation network), in information science and bibliometrics, is a directed graph that describes the citations within a collection of documents.
Each vertex (or node) in the graph represents a document in the collection, and each edge is directed from one document toward another that it cites (or vice versa depending on the specific implementation).[1]
Citation graphs have been utilised in various ways, including forms of citation analysis, academic search tools and court judgements. They are predicted to become more relevant and useful in the future as the body of published research grows.
Implementation
[edit]There is no standard format for the citations in bibliographies, and the record linkage of citations can be a time-consuming and complicated process. Furthermore, citation errors can occur at any stage of the publishing process. However, there is a long history of creating citation databases, also known as citation indexes, so there is a lot of information about such problems.
In principle, each document should have a unique publication date and can only refer to earlier documents. This means that an ideal citation graph is not only directed but acyclic; that is, there are no loops in the graph. This is not always the case in practice, since an academic paper goes through several versions in the publishing process. The timing of asynchronous updates to bibliographies may lead to edges that apparently point backward in time. Such "backward" citations seem to constitute less than 1% of the total number of links.[2]
As citation links are meant to be permanent, the bulk of a citation graph should be static, and only the leading edge of the graph should change. Exceptions might occur when papers are withdrawn from circulation.[2]
Background and history
[edit]A citation is a reference to a published or unpublished source (not always the original source). More precisely, a citation is an abbreviated alphanumeric expression embedded in the body of an intellectual work that denotes an entry in the bibliographic references section of the work. Its purpose is to acknowledge the relevance of the works of others to the topic of discussion at the point where the citation appears.
Generally the combination of both the in-body citation and the bibliographic entry constitutes what is commonly thought of as a citation (whereas bibliographic entries by themselves are not).[3] References to single, machine-readable assertions in electronic scientific articles are known as nanopublications, a form of micro attributions.
Citation networks are one kind of social network that has been studied quantitatively almost from the moment citation databases first became available. In 1965, Derek J. de Solla Price described the inherent linking characteristic of the Science Citation Index (SCI) in his paper entitled "Networks of Scientific Papers." The links between citing and cited papers became dynamic when the SCI began to be published online. In 1973, Henry Small published his work on co-citation analysis, which became a self-organizing classification system that led to document clustering experiments and eventually what is called "Research Reviews."[4]
Applications
[edit]Citation Analysis
[edit]Citation graphs can be applied to measures of scholarly impact, the impact a particular paper has had on the academic world. While a hard value to quantify, scholarly impact is useful, as having a measure of scholarly impact for many papers can aid in identifying important papers. It can also provide a measure of the relevance of a particular academic community. Citation graphs are very useful in measuring this as the number of connections on the citation graph corresponds with the scholarly impact of an article, as this means it has been cited by many other papers.[5]
Similarity analysis is another area of citation analysis which frequently makes uses of citation graphs. The relationship between two papers in the citation graph has been compared to their text-based similarity, and it is found that closeness in the citation graph can predict a level of text-based similarity.[6] Additionally, it has been found that the two methods – citation graph closeness and traditional content-based similarity – work well in conjunction to produce a more accurate result.[6]
Analyses of citation graphs have also led to the proposal of the citation graph as a way to identify different communities and research areas within the academic world. It has been found that analysing the citation graph for groups of documents in conjunction with keywords can provide an accurate way to identify clusters of similar research.[7] In a similar vein, a way of identifying the main “stream” of an area of research, or the progression of a research idea over time can be identified by using depth first search algorithms on the citation graph. Instead of looking at similarity between two nodes, or clusters of many nodes, this method instead goes through the links between nodes to trace a research idea back to its beginning, and so discover its progression through different papers to where its current status is.[8]
Search Tools
[edit]The traditional method used by academic search tools is to check for matches between a search term and keywords in papers to return potential matches. While mostly effective, this method can lead to errors where a paper is recommended from a different discipline because of keyword matches even when the two topics actually have little in common.
Many have argued that this way of searching for relevant papers could be improved and made more accurate if citation graphs were incorporated into academic paper search tools. For example, one system was proposed which used both the keyword system and a popularity system based on how many connections a paper had in the citation graph. In this system, more connected papers were considered more popular and therefore given a higher weighting in the paper recommendation system.[9]
In more recent years, visual search tools have been developed which use citation graphs to provide a visual representation of the connections between papers. A commercial implementation of this concept is the search tool Connected Papers.[citation needed]
Court Judgements
[edit]Citation graphs have a history of being used to aid in organising and mapping citations of legal documents. In a similar way to the aforementioned search tools, constructions of citation graphs specific to the types of citations found in legal documents have been used to allow relevant past legal documents to be found when needed for a court decision. As a way of replacing or improving upon traditional search methods, this citation graph aided way of organising legal documents can provide higher efficiency, accuracy, and organisation.[10]
Related networks
[edit]There are several other types of network graphs that are closely related to citation networks. The co-citation graph is the graph between documents as nodes, where two documents are connected if they share a common citation (see Co-citation and Bibliographic coupling). Other related networks are formed using other information present in the document. For instance, in a collaboration graph, known in this context as a co-authorship network, the nodes are the authors of documents, linked if they have co-authored the same document. The link weights between two authors in co-authorship networks can increase over time if they have further collaboration.
Future Developments
[edit]While citation graphs have had a noticeable impact on several areas of academia, they are likely to become more relevant in the future. As the body of published research grows, more traditional ways of searching for papers will become less effective in narrowing down relevant papers to a particular topic. For example, text-based similarity can only go so far in selecting which papers are relevant to a topic, whereas the addition of citation graphs could make use of giving higher priority to those papers which have a lot of connections to other papers relevant to the topic.
However, developments like this face similar challenges to that of most applications of citation graphs, which is the face that there is no standardized format or way of citing. This makes the construction of these graphs very difficult, since it requires complex software analysis to extract citations from papers. One solution proposed to this problem is to create open databases of citation information in a format which could be used by anyone and easily converted to a different form, for example a citation graph.[11]
See also
[edit]- Collaboration graph, a graph defined by the authors of documents
- Web graph, a citation graph of references from one web page to another in the World Wide Web
- Directed Acyclic Graph, the formal mathematical structure of a well-constructed citation graph
- Legal citation analysis citation analysis in legal contexts
References
[edit]- ^ Egghe, Leo; Rousseau, Ronald (1990). Introduction to Informetrics : quantitative methods in library, documentation and information science. Amsterdam, the Netherlands: Elsevier Science Publishers. p. 228. ISBN 0-444-88493-9.
- ^ a b James R Clough; Jamie Gollings; Tamar V Loach; Tim S Evans (2015). "Transitive reduction of citation networks". Journal of Complex Networks. 3 (2): 189–203. arXiv:1310.8224. doi:10.1093/comnet/cnu039. S2CID 10228152.
- ^ Zhao, Dangzhi; Strotmann, Andreas (2015-02-01). Analysis and Visualization of Citation Networks. Morgan & Claypool Publishers. ISBN 978-1-60845-939-1.
- ^ Structures and Statistics of Citation Networks, Miray Kas
- ^ Życzkowski, Karol (2010-10-01). "Citation graph, weighted impact factors and performance indices". Scientometrics. 85 (1): 301–315. arXiv:0904.2110. doi:10.1007/s11192-010-0208-6. ISSN 1588-2861. S2CID 7614954.
- ^ a b Lu, Wangzhong; Janssen, J.; Milios, E.; Japkowicz, N.; Zhang, Yongzheng (2007-01-01). "Node similarity in the citation graph". Knowledge and Information Systems. 11 (1): 105–129. doi:10.1007/s10115-006-0023-9. ISSN 0219-3116. S2CID 26234247.
- ^ Bolelli, Levent; Ertekin, Seyda; Giles, C. Lee (2006). "Clustering Scientific Literature Using Sparse Citation Graph Analysis". In Fürnkranz, Johannes; Scheffer, Tobias; Spiliopoulou, Myra (eds.). Knowledge Discovery in Databases: PKDD 2006. Lecture Notes in Computer Science. Vol. 4213. Berlin, Heidelberg: Springer. pp. 30–41. doi:10.1007/11871637_8. ISBN 978-3-540-46048-0. S2CID 15527080.
- ^ Hummon, Norman P.; Dereian, Patrick (1989-03-01). "Connectivity in a citation network: The development of DNA theory". Social Networks. 11 (1): 39–63. doi:10.1016/0378-8733(89)90017-8. ISSN 0378-8733.
- ^ Liu, Hanwen; Kou, Huaizhen; Yan, Chao; Qi, Lianyong (2020-04-24). "Keywords-Driven and Popularity-Aware Paper Recommendation Based on Undirected Paper Citation Graph". Complexity. 2020: e2085638. doi:10.1155/2020/2085638. ISSN 1076-2787.
- ^ Sadeghian, Ali; Sundaram, Laksshman; Wang, Daisy Zhe; Hamilton, William F.; Branting, Karl; Pfeifer, Craig (June 2018). "Automatic semantic edge labeling over legal citation graphs". Artificial Intelligence and Law. 26 (2): 127–144. doi:10.1007/s10506-018-9217-1. ISSN 0924-8463. S2CID 254266762.
- ^ Lauscher, Anne; Eckert, Kai; Galke, Lukas; Scherp, Ansgar; Rizvi, Syed Tahseen Raza; Ahmed, Sheraz; Dengel, Andreas; Zumstein, Philipp; Klein, Annette (2018-05-23). "Linked Open Citation Database". Proceedings of the 18th ACM/IEEE on Joint Conference on Digital Libraries (PDF). JCDL '18. New York, NY, USA: Association for Computing Machinery. pp. 109–118. doi:10.1145/3197026.3197050. ISBN 978-1-4503-5178-2. S2CID 4902279.
Further reading
[edit]- An, Yuan; Janssen, Jeannette; Milios, Evangelos E. (2004), "Characterizing and Mining the Citation Graph of the Computer Science Literature", Knowledge and Information Systems, 6 (6): 664–678, doi:10.1007/s10115-003-0128-3, S2CID 348227.
- Yong, Fang; Rousseau, Ronald (2001), "Lattices in citation networks: An investigation into the structure of citation graphs", Scientometrics, 50 (2): 273–287, doi:10.1023/A:1010573723540, S2CID 413673.
- Lu, Wangzhong; Janssen, J.; Milios, E.; Japkowicz, N.; Zhang, Yongzheng (2007), "Node similarity in the citation graph", Knowledge and Information Systems, 11 (1): 105–129, doi:10.1007/s10115-006-0023-9, S2CID 26234247.
