Competitive inhibition

2H
5OH) serves as a competitive inhibitor to methanol (CH
3OH) and ethylene glycol ((CH2OH)2) for the enzyme alcohol dehydrogenase in the liver when present in large amounts. For this reason, ethanol is sometimes used as a means to treat or prevent toxicity following accidental ingestion of these chemicals.
Competitive inhibition is interruption of a chemical pathway owing to one chemical substance inhibiting the effect of another by competing with it for binding or bonding. Any metabolic or chemical messenger system can potentially be affected by this principle, but several classes of competitive inhibition are especially important in biochemistry and medicine, including the competitive form of enzyme inhibition, the competitive form of receptor antagonism, the competitive form of antimetabolite activity, and the competitive form of poisoning (which can include any of the aforementioned types).
Enzyme inhibition type
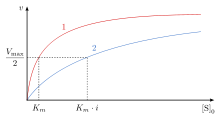
[edit]In competitive inhibition of enzyme catalysis, binding of an inhibitor prevents binding of the target molecule of the enzyme, also known as the substrate.[1] This is accomplished by blocking the binding site of the substrate – the active site – by some means. The Vmax indicates the maximum velocity of the reaction, while the Km is the amount of substrate needed to reach half of the Vmax. Km also plays a part in indicating the tendency of the substrate to bind the enzyme.[2] Competitive inhibition can be overcome by adding more substrate to the reaction, which increases the chances of the enzyme and substrate binding. As a result, competitive inhibition alters only the Km, leaving the Vmax the same.[3] This can be demonstrated using enzyme kinetics plots such as the Michaelis–Menten or the Lineweaver-Burk plot. Once the inhibitor is bound to the enzyme, the slope will be affected, as the Km either increases or decreases from the original Km of the reaction.[4][5][6]
Most competitive inhibitors function by binding reversibly to the active site of the enzyme.[1] As a result, many sources state that this is the defining feature of competitive inhibitors.[7] This, however, is a misleading oversimplification, as there are many possible mechanisms by which an enzyme may bind either the inhibitor or the substrate but never both at the same time.[1] For example, allosteric inhibitors may display competitive, non-competitive, or uncompetitive inhibition.[1]
Mechanism
[edit]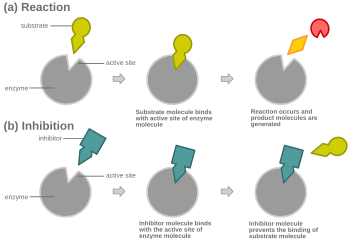
In competitive inhibition, an inhibitor that resembles the normal substrate binds to the enzyme, usually at the active site, and prevents the substrate from binding.[8] At any given moment, the enzyme may be bound to the inhibitor, the substrate, or neither, but it cannot bind both at the same time. During competitive inhibition, the inhibitor and substrate compete for the active site. The active site is a region on an enzyme to which a particular protein or substrate can bind. The active site will thus only allow one of the two complexes to bind to the site, either allowing a reaction to occur or yielding it. In competitive inhibition, the inhibitor resembles the substrate, taking its place and binding to the active site of an enzyme. Increasing the substrate concentration would diminish the "competition" for the substrate to properly bind to the active site and allow a reaction to occur.[3] When the substrate is of higher concentration than the concentration of the competitive inhibitor, it is more probable that the substrate will come into contact with the enzyme's active site than with the inhibitor's.
Competitive inhibitors are commonly used to make pharmaceuticals.[3] For example, methotrexate is a chemotherapy drug that acts as a competitive inhibitor. It is structurally similar to the coenzyme, folate, which binds to the enzyme dihydrofolate reductase.[3] This enzyme is part of the synthesis of DNA and RNA, and when methotrexate binds the enzyme, it renders it inactive, so that it cannot synthesize DNA and RNA.[3] The cancer cells are thus unable to grow and divide. Another example: prostaglandin are made in large amounts as a response to pain and can cause inflammation. Essential fatty acids form the prostaglandins; when this was discovered, it turned out that these were actually very good inhibitors to prostaglandins. These fatty acids inhibitors have been used as drugs to relieve pain because they can act as the substrate, and bind to the enzyme, and block prostaglandins.[9]
An example of non-drug related competitive inhibition is in the prevention of browning of fruits and vegetables. For example, tyrosinase, an enzyme within mushrooms, normally binds to the substrate, monophenols, and forms brown o-quinones.[10] Competitive substrates, such as 4-substituted benzaldehydes for mushrooms, compete with the substrate lowering the amount of the monophenols that bind. These inhibitory compounds added to the produce keep it fresh for longer periods of time by decreasing the binding of the monophenols that cause browning.[10] This allows for an increase in produce quality as well as shelf life.
Competitive inhibition can be reversible or irreversible. If it is reversible inhibition, then effects of the inhibitor can be overcome by increasing substrate concentration.[8] If it is irreversible, the only way to overcome it is to produce more of the target (and typically degrade and/or excrete the irreversibly inhibited target).
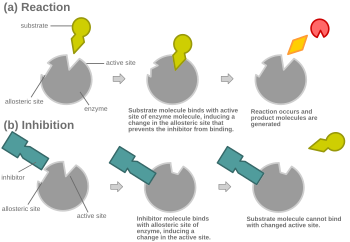
In virtually every case, competitive inhibitors bind in the same binding site (active site) as the substrate, but same-site binding is not a requirement. A competitive inhibitor could bind to an allosteric site of the free enzyme and prevent substrate binding, as long as it does not bind to the allosteric site when the substrate is bound. For example, strychnine acts as an allosteric inhibitor of the glycine receptor in the mammalian spinal cord and brain stem. Glycine is a major post-synaptic inhibitory neurotransmitter with a specific receptor site. Strychnine binds to an alternate site that reduces the affinity of the glycine receptor for glycine, resulting in convulsions due to lessened inhibition by the glycine.[11]
In competitive inhibition, the maximum velocity () of the reaction is unchanged, while the apparent affinity of the substrate to the binding site is decreased (the dissociation constant is apparently increased). The change in (Michaelis–Menten constant) is parallel to the alteration in , as one increases the other must decrease. When a competitive inhibitor is bound to an enzyme the increases. This means the binding affinity for the enzyme is decreased, but it can be overcome by increasing the concentration of the substrate.[12] Any given competitive inhibitor concentration can be overcome by increasing the substrate concentration. In that case, the substrate will reduce the availability for an inhibitor to bind, and, thus, outcompete the inhibitor in binding to the enzyme.[12]

Biological examples
[edit]After an accidental ingestion of a contaminated opioid drug desmethylprodine, the neurotoxic effect of 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP) was discovered. MPTP is able to cross the blood brain barrier and enter acidic lysosomes.[13] MPTP is biologically activated by MAO-B, an isozyme of monoamine oxidase (MAO) which is mainly concentrated in neurological disorders and diseases.[14] Later, it was discovered that MPTP causes symptoms similar to that of Parkinson's disease. Cells in the central nervous system (astrocytes) include MAO-B that oxidizes MPTP to 1-methyl-4-phenylpyridinium (MPP+), which is toxic.[13] MPP+ eventually travels to the extracellular fluid by a dopamine transporter, which ultimately causes the Parkinson's symptoms. However, competitive inhibition of the MAO-B enzyme or the dopamine transporter protects against the oxidation of MPTP to MPP+. A few compounds have been tested for their ability to inhibit oxidation of MPTP to MPP+ including methylene blue, 5-nitroindazole, norharman, 9-methylnorharman, and menadione.[14] These demonstrated a reduction of neurotoxicity produced by MPTP.

Sulfa drugs also act as competitive inhibitors. For example, sulfanilamide competitively binds to the enzyme in the dihydropteroate synthase (DHPS) active site by mimicking the substrate para-aminobenzoic acid (PABA).[15] This prevents the substrate itself from binding which halts the production of folic acid, an essential nutrient. Bacteria must synthesize folic acid because they do not have a transporter for it. Without folic acid, bacteria cannot grow and divide. Therefore, because of sulfa drugs' competitive inhibition, they are excellent antibacterial agents. An example of competitive inhibition was demonstrated experimentally for the enzyme succinic dehydrogenase, which catalyzes the oxidation of succinate to fumarate in the Krebs cycle. Malonate is a competitive inhibitor of succinic dehydrogenase. The binding of succinic dehydrogenase to the substrate, succinate, is competitively inhibited. This happens because malonate's chemistry is similar to succinate. Malonate's ability to inhibit binding of the enzyme and substrate is based on the ratio of malonate to succinate. Malonate binds to the active site of succinic dehydrogenase so that succinate cannot. Thus, it inhibits the reaction.[16]
Equation
[edit]The Michaelis–Menten Model can be an invaluable tool to understanding enzyme kinetics. According to this model, a plot of the reaction velocity (V0) associated with the concentration [S] of the substrate can then be used to determine values such as Vmax, initial velocity, and Km (Vmax/2 or affinity of enzyme to substrate complex).[4]
Competitive inhibition increases the apparent value of the Michaelis–Menten constant, , such that initial rate of reaction, , is given by
where , is the inhibitor's dissociation constant and is the inhibitor concentration.
remains the same because the presence of the inhibitor can be overcome by higher substrate concentrations. , the substrate concentration that is needed to reach , increases with the presence of a competitive inhibitor. This is because the concentration of substrate needed to reach with an inhibitor is greater than the concentration of substrate needed to reach without an inhibitor.
Derivation
[edit]In the simplest case of a single-substrate enzyme obeying Michaelis–Menten kinetics, the typical scheme
is modified to include binding of the inhibitor to the free enzyme:
Note that the inhibitor does not bind to the ES complex and the substrate does not bind to the EI complex. It is generally assumed that this behavior is indicative of both compounds binding at the same site, but that is not strictly necessary. As with the derivation of the Michaelis–Menten equation, assume that the system is at steady-state, i.e. the concentration of each of the enzyme species is not changing.
Furthermore, the known total enzyme concentration is , and the velocity is measured under conditions in which the substrate and inhibitor concentrations do not change substantially and an insignificant amount of product has accumulated.
We can therefore set up a system of equations:
| (1) |
| (2) |
| (3) |
| (4) |
where and are known. The initial velocity is defined as , so we need to define the unknown in terms of the knowns and .
From equation (3), we can define E in terms of ES by rearranging to
Dividing by gives
As in the derivation of the Michaelis–Menten equation, the term can be replaced by the macroscopic rate constant :
| (5) |
Substituting equation (5) into equation (4), we have
Rearranging, we find that
At this point, we can define the dissociation constant for the inhibitor as , giving
| (6) |
At this point, substitute equation (5) and equation (6) into equation (1):
Rearranging to solve for ES, we find
| (7) |
Returning to our expression for , we now have:
Since the velocity is maximal when all the enzyme is bound as the enzyme-substrate complex, . Replacing and combining terms finally yields the conventional form:
| (8) |
To compute the concentration of competitive inhibitor that yields a fraction of velocity where :
| (9) |
See also
[edit]- Schild regression for ligand receptor inhibition
- Non-competitive inhibition
Notes and references
[edit]- ^ a b c d "Types of Inhibition". NIH Center for Translational Therapeutics. Archived from the original on 8 September 2011. Retrieved 2 April 2012.
- ^ Lodish H, Berk A, Zipursky SL, Matsudaira P, Baltimore D, Darnell J (2000). "Functional Design of Proteins". Molecular Cell Biology (4th ed.).
- ^ a b c d e Berg JM, Tymoczko JL, Stryer L (2002). "Enzymes Can Be Inhibited by Specific Molecules". Biochemistry (5th ed.).
- ^ a b Berg JM, Tymoczko JL, Stryer L (2002). "The Michaelis–Menten Model Accounts for the Kinetic Properties of Many Enzymes". Biochemistry (5th ed.).
- ^ Eadie SG (1942). "The Inhibition of Cholinesterase by Physostigmine and Prostigmine". Journal of Biological Chemistry. 146: 85–93. doi:10.1016/S0021-9258(18)72452-6.
- ^ Berg JM, Tymoczko JL, Stryer L (2002). "Appendix: Vmax and KM Can Be Determined by Double-Reciprocal Plots". Biochemistry (5th ed.).
- ^ Ophardt C. "Virtual Chembook". Elmhurst College. Archived from the original on 17 October 2015. Retrieved 1 September 2015.
- ^ a b "Map: Biochemistry Free & Easy (Ahern and Rajagopal)". Biology LibreTexts. 24 December 2014. Retrieved 2 November 2017.
- ^ Flower RJ (March 1974). "Drugs which inhibit prostaglandin biosynthesis". Pharmacological Reviews. 26 (1): 33–67. PMID 4208101.
- ^ a b Jiménez M, Chazarra S, Escribano J, Cabanes J, García-Carmona F (August 2001). "Competitive inhibition of mushroom tyrosinase by 4-substituted benzaldehydes". Journal of Agricultural and Food Chemistry. 49 (8): 4060–4063. doi:10.1021/jf010194h. PMID 11513710.
- ^ Dick RM (2011). "Chapter 2. Pharmacodynamics: The Study of Drug Action". In Ouellette R, Joyce JA (eds.). Pharmacology for Nurse Anesthesiology. Jones & Bartlett Learning. ISBN 978-0-7637-8607-6.
- ^ a b Voet D, Voet JG, Pratt CW (29 February 2016). Fundamentals of biochemistry : life at the molecular level (Fifth ed.). Hoboken, NJ. ISBN 9781118918401. OCLC 910538334.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ a b Sian J, Youdim MB, Riederer P, Gerlach M (1999). "MPTP-Induced Parkinsonian Syndrome". Basic Neurochemistry: Molecular, Cellular and Medical Aspects. 6th Edition.
- ^ a b Herraiz T, Guillén H (August 2011). "Inhibition of the bioactivation of the neurotoxin MPTP by antioxidants, redox agents and monoamine oxidase inhibitors". Food and Chemical Toxicology. 49 (8): 1773–1781. doi:10.1016/j.fct.2011.04.026. hdl:10261/63126. PMID 21554916.
- ^ "How Sulfa Drugs Work". National Institutes of Health (NIH). 15 May 2015. Retrieved 2 November 2017.
- ^ Potter VR, Dubois KP (March 1943). "Studies on the Mechanism of Hydrogen Transport in Animal Tissues". The Journal of General Physiology. 26 (4): 391–404. doi:10.1085/jgp.26.4.391. PMC 2142566. PMID 19873352.






![{\displaystyle V_{0}={\frac {V_{\max }\,[S]}{K_{m}^{\text{app}}+[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e6ea985b759c13c54c08b2e1a1f7b292c549beb)
![{\displaystyle K_{m}^{\text{app}}=K_{m}(1+[I]/K_{i})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e013bb3d416acd07c0c55ee196d46e9ede190a63)

![{\displaystyle [I]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5962300a54e8ce8b5761dac9a5fbbca450c2ce0f)

![{\displaystyle {\ce {E + S <=>[k_1][k_{-1}] ES ->[k_2] E + P}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa34fa0b8ef16e2c4886b79b41fd6a84e83a68fd)
![{\displaystyle {\ce {EI + S <=>[k_{-3}][k_3] E + S + I <=>[k_1][k_{-1}] ES + I ->[k_2] E + P + I}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c358fddd797429f33b9c778a4bf4f669e8000b0)
![{\displaystyle {\frac {d[{\ce {E}}]}{dt}}={\frac {d[{\ce {ES}}]}{dt}}={\frac {d[{\ce {EI}}]}{dt}}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d5d8b4f228bd04aff5488c2efbc9f11f6a27a4b)
![{\displaystyle [{\ce {E}}]_{0}=[{\ce {E}}]+[{\ce {ES}}]+[{\ce {EI}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee7863f535867e7f0b9e3619c9d5431b8d14851a)
![{\displaystyle {\frac {d[{\ce {E}}]}{dt}}=0=-k_{1}[{\ce {E}}][{\ce {S}}]+k_{-1}[{\ce {ES}}]+k_{2}[{\ce {ES}}]-k_{3}[{\ce {E}}][{\ce {I}}]+k_{-3}[{\ce {EI}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/524f829178a7d543a7f1dfe0d3836d3f2cd9beca)
![{\displaystyle {\frac {d[{\ce {ES}}]}{dt}}=0=k_{1}[{\ce {E}}][{\ce {S}}]-k_{-1}[{\ce {ES}}]-k_{2}[{\ce {ES}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/deee1b4eb1dae3e5957260a6e625632daa130b8c)
![{\displaystyle {\frac {d[{\ce {EI}}]}{dt}}=0=k_{3}[{\ce {E}}][{\ce {I}}]-k_{-3}[EI]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/632d3667fd0a9b85d3e0572d171e0ee8b67e8668)
![{\displaystyle {\ce {[S], [I]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ec1dbaad807d3af650d3805d798ed15120624bd)
![{\displaystyle {\ce {[E]_0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a654ad516b5d2547fd9980bb7590464441d6c38)
![{\displaystyle V_{0}=d[{\ce {P}}]/dt=k_{2}[{\ce {ES}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cee1a793ade4b98a68c506615766985cb243899)
![{\displaystyle {\ce {[ES]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a96c38a14c944f4ae51601cd8670fd2bf8e12331)
![{\displaystyle k_{1}[{\ce {E}}][{\ce {S}}]=(k_{-1}+k_{2})[{\ce {ES}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/940c092e01999c100f4d5fff6650b39dff53de02)
![{\displaystyle k_{1}[{\ce {S}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28690106a4f72a9371157eefe3e178d952cb36f0)
![{\displaystyle [{\ce {E}}]={\frac {(k_{-1}+k_{2})[{\ce {ES}}]}{k_{1}[{\ce {S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41cd11072115b7e97377d2dc62bd80a0e9460cd5)

![{\displaystyle [{\ce {E}}]={\frac {K_{m}[{\ce {ES}}]}{\ce {[S]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5caf94a9df39bcbeae36e01bfcd1f48e27626ce9)
![{\displaystyle 0={\frac {k_{3}[{\ce {I}}]K_{m}[{\ce {ES}}]}{\ce {[S]}}}-k_{-3}[{\ce {EI}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3612eb7c921915246bb9dd47363904140d563374)
![{\displaystyle [{\ce {EI}}]={\frac {K_{m}k_{3}[{\ce {I}}][{\ce {ES}}]}{k_{-3}[{\ce {S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5e8681d305f3fa55e808a5c06fad3748f06e131)

![{\displaystyle [{\ce {EI}}]={\frac {K_{m}[{\ce {I}}][{\ce {ES}}]}{K_{i}[{\ce {S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b5b6d93be687b516fc668d4934ac27e5972ae30)
![{\displaystyle [{\ce {E}}]_{0}={\frac {K_{m}[{\ce {ES}}]}{\ce {[S]}}}+[{\ce {ES}}]+{\frac {K_{m}[{\ce {I}}][{\ce {ES}}]}{K_{i}[{\ce {S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68c1417ec7ba5d7255a28927ed40932af9323e01)
![{\displaystyle [{\ce {E}}]_{0}=[{\ce {ES}}]\left({\frac {K_{m}}{\ce {[S]}}}+1+{\frac {K_{m}[{\ce {I}}]}{K_{i}[{\ce {S}}]}}\right)=[{\ce {ES}}]{\frac {K_{m}K_{i}+K_{i}[{\ce {S}}]+K_{m}[{\ce {I}}]}{K_{i}[{\ce {S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2691e0b26e6bee9fe37253403c892909a07add45)
![{\displaystyle [{\ce {ES}}]={\frac {K_{i}[{\ce {S}}][{\ce {E}}]_{0}}{K_{m}K_{i}+K_{i}[{\ce {S}}]+K_{m}[{\ce {I}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b57aff644fb93ec40ef3663d1463f25ea158869e)
![{\displaystyle V_{0}=k_{2}[{\ce {ES}}]={\frac {k_{2}K_{i}[{\ce {S}}][{\ce {E}}]_{0}}{K_{m}K_{i}+K_{i}[{\ce {S}}]+K_{m}[{\ce {I}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7548c901ebd2e13620f6c9c6c30510ad5365859)
![{\displaystyle V_{0}={\frac {k_{2}[{\ce {E}}]_{0}[{\ce {S}}]}{K_{m}+[{\ce {S}}]+K_{m}{\frac {[{\ce {I}}]}{K_{i}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83cb5b38fc5e1ea8d7df09f1f8fec2d8f47db635)
![{\displaystyle V_{\max }=k_{2}[{\ce {E}}]_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ea107b2c44540b990daab7f21c8a35fc76f6476)
![{\displaystyle V_{0}={\frac {V_{\max }[{\ce {S}}]}{K_{m}\left(1+{\frac {[{\ce {I}}]}{K_{i}}}\right)+[{\ce {S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09a841f4777fa07f79bcec43de7264e95ef8f57c)
![{\displaystyle {\ce {[I]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da716928de5f662f6ff1a1fc9ec0bde65f3fe2c2)


![{\displaystyle [{\ce {I}}]=\left({\frac {1}{f_{V{_{0}}}}}-1\right)K_{i}\left(1+{\frac {[{\ce {S}}]}{K_{m}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccc99438e12f1dfdd4bdbdd0b21637c4003c470f)