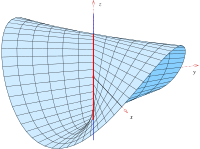
Conoid

In geometry a conoid (from Greek κωνος 'cone' and -ειδης 'similar') is a ruled surface, whose rulings (lines) fulfill the additional conditions:
- (1) All rulings are parallel to a plane, the directrix plane.
- (2) All rulings intersect a fixed line, the axis.
The conoid is a right conoid if its axis is perpendicular to its directrix plane. Hence all rulings are perpendicular to the axis.
Because of (1) any conoid is a Catalan surface and can be represented parametrically by
Any curve x(u0,v) with fixed parameter u = u0 is a ruling, c(u) describes the directrix and the vectors r(u) are all parallel to the directrix plane. The planarity of the vectors r(u) can be represented by
- .
If the directrix is a circle, the conoid is called a circular conoid.
The term conoid was already used by Archimedes in his treatise On Conoids and Spheroides.
Examples
[edit]Right circular conoid
[edit]The parametric representation
- describes a right circular conoid with the unit circle of the x-y-plane as directrix and a directrix plane, which is parallel to the y--z-plane. Its axis is the line
Special features:
- The intersection with a horizontal plane is an ellipse.
- is an implicit representation. Hence the right circular conoid is a surface of degree 4.
- Kepler's rule gives for a right circular conoid with radius and height the exact volume: .
The implicit representation is fulfilled by the points of the line , too. For these points there exist no tangent planes. Such points are called singular.
Parabolic conoid
[edit]
The parametric representation
describes a parabolic conoid with the equation . The conoid has a parabola as directrix, the y-axis as axis and a plane parallel to the x-z-plane as directrix plane. It is used by architects as roof surface (s. below).
The parabolic conoid has no singular points.
Further examples
[edit]-
hyperbolic paraboloid
-
Plücker conoid
-
Whitney umbrella
Applications
[edit]

Mathematics
[edit]There are a lot of conoids with singular points, which are investigated in algebraic geometry.
Architecture
[edit]Like other ruled surfaces conoids are of high interest with architects, because they can be built using beams or bars. Right conoids can be manufactured easily: one threads bars onto an axis such that they can be rotated around this axis, only. Afterwards one deflects the bars by a directrix and generates a conoid (s. parabolic conoid).
External links
[edit]- mathworld: Plücker conoid
- "Conoid", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
References
[edit]- A. Gray, E. Abbena, S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, 3rd ed. Boca Raton, FL:CRC Press, 2006. [1] (ISBN 978-1-58488-448-4)
- Vladimir Y. Rovenskii, Geometry of curves and surfaces with MAPLE [2] (ISBN 978-0-8176-4074-3)