Coxeter element

Not to be confused with Longest element of a Coxeter group.

In mathematics, the Coxeter number h is the order of a Coxeter element of an irreducible Coxeter group. It is named after H.S.M. Coxeter.

Definitions

Note that this article assumes a finite Coxeter group. For infinite Coxeter groups, there are multiple conjugacy classes of Coxeter elements, and they have infinite order.

There are many different ways to define the Coxeter number h of an irreducible root system.

A Coxeter element is a product of all simple reflections. The product depends on the order in which they are taken, but different orderings produce conjugate elements, which have the same order.

• The Coxeter number is the number of roots divided by the rank. The number of reflections in the Coxeter group is half the number of roots.
• The Coxeter number is the order of any Coxeter element;.
• If the highest root is ∑m_iα_i for simple roots α_i, then the Coxeter number is 1 + ∑m_i
• The Coxeter number is the dimension of the corresponding Lie algebra is n(h + 1), where n is the rank and h is the Coxeter number.
• The Coxeter number is the highest degree of a fundamental invariant of the Coxeter group acting on polynomials.
• The Coxeter number is given by the following table:

Coxeter group		Coxeter diagram	Dynkin diagram	Coxeter number h	Dual Coxeter number	Degrees of fundamental invariants
An	[3,3...,3]	...	...	n + 1	n + 1	2, 3, 4, ..., n + 1
Bn	[4,3...,3]	...	...	2n	2n − 1	2, 4, 6, ..., 2n
Cn			...		n + 1
Dn	[3,3,..31,1]	...	...	2n − 2	2n − 2	n; 2, 4, 6, ..., 2n − 2
E6	[32,2,1]			12	12	2, 5, 6, 8, 9, 12
E7	[33,2,1]			18	18	2, 6, 8, 10, 12, 14, 18
E8	[34,2,1]			30	30	2, 8, 12, 14, 18, 20, 24, 30
F4	[3,4,3]			12	9	2, 6, 8, 12
G2	[6]			6	4	2, 6
H3	[5,3]		-	10		2, 6, 10
H4	[5,3,3]		-	30		2, 12, 20, 30
I2(p)	[p]		-	p		2, p

The invariants of the Coxeter group acting on polynomials form a polynomial algebra whose generators are the fundamental invariants; their degrees are given in the table above. Notice that if m is a degree of a fundamental invariant then so is h + 2 − m.

The eigenvalues of a Coxeter element are the numbers e^{2πi(m − 1)/h} as m runs through the degrees of the fundamental invariants. Since this starts with m = 2, these include the primitive hth root of unity, ζ_h = e^2πi/h, which is important in the Coxeter plane, below.

Group order

There are relations between group order, g, and the Coxeter number, h:

• [p]: 2h/g_p = 1
• [p,q]: 8/g_p,q = 2/p + 2/q -1
• [p,q,r]: 64h/g_p,q,r = 12 - p - 2q - r + 4/p + 4/r
• [p,q,r,s]: 16/g_p,q,r,s = 8/g_p,q,r + 8/g_q,r,s + 2/(ps) - 1/p - 1/q - 1/r - 1/s +1
• ...

An example, [3,3,5] has h=30, so 64*30/g = 12 - 3 - 6 - 5 + 4/3 + 4/5 = 2/15, so g = 1920*15/2= 960*15 = 14400.

Coxeter elements

Coxeter elements of $A_{n-1}\cong S_{n}$, considered as the symmetric group on n elements, are n-cycles: for simple reflections the adjacent transpositions $(1,2),(2,3),\dots$, a Coxeter element is the n-cycle $(1,2,3,\dots ,n)$.

The dihedral group Dih_m is generated by two reflections that form an angle of $2\pi /2m$, and thus their product is a rotation by $2\pi /m$.

Coxeter plane

Projection of E₈ root system onto Coxeter plane, showing 30-fold symmetry.

For a given Coxeter element w, there is a unique plane P on which w acts by rotation by 2π/h. This is called the Coxeter plane and is the plane on which P has eigenvalues e^2πi/h and e^−2πi/h = e^{2πi(h−1)/h}. This plane was first systematically studied in (Coxeter 1948), and subsequently used in (Steinberg 1959) to provide uniform proofs about properties of Coxeter elements.

The Coxeter plane is often used to draw diagrams of higher-dimensional polytopes and root systems – the vertices and edges of the polytope, or roots (and some edges connecting these) are orthogonally projected onto the Coxeter plane, yielding a Petrie polygon with h-fold rotational symmetry. For root systems, no root maps to zero, corresponding to the Coxeter element not fixing any root or rather axis (not having eigenvalue 1 or −1), so the projections of orbits under w form h-fold circular arrangements and there is an empty center, as in the E₈ diagram at above right. For polytopes, a vertex may map to zero, as depicted below. Projections onto the Coxeter plane are depicted below for the Platonic solids.

In three dimensions, the symmetry of a regular polyhedron, {p,q}, with one directed petrie polygon marked, defined as a composite of 3 reflections, has rotoinversion symmetry S_h, [2⁺,h⁺], order h. Adding a mirror, the symmetry can be doubled to antiprismatic symmetry, D_hd, [2⁺,h], order 2h. In orthogonal 2D projection, this becomes dihedral symmetry, Dih_h, [h], order 2h.

Coxeter group	A3, [3,3] Td	B3, [4,3] Oh		H3, [5,3] Th
Regular polyhedron	{3,3}	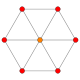{4,3}	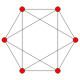{3,4}	{5,3}	{3,5}
Symmetry	S4, [2+,4+], (2×) D2d, [2+,4], (2*2)	S6, [2+,6+], (3×) D3d, [2+,6], (2*3)		S10, [2+,10+], (5×) D5d, [2+,10], (2*5)
Coxeter plane symmetry	Dih4, [4], (*4•)	Dih6, [6], (*6•)		Dih10, [10], (*10•)
Petrie polygons of the Platonic solids, showing 4-fold, 6-fold, and 10-fold symmetry.

In four dimension, the symmetry of a regular polychoron, {p,q,r}, with one directed petrie polygon marked is a double rotation, defined as a composite of 4 reflections, with symmetry +¹/_h[C_h×C_h] (John H. Conway), (C_2h/C₁;C_2h/C₁) (#1', Patrick du Val (1964)), order h.

Coxeter group	A4, [3,3,3]	B4, [4,3,3]		F4, [3,4,3]	H4, [5,3,3]
Regular polychoron	{3,3,3}	{3,3,4}	{4,3,3}	{3,4,3}	{5,3,3}	{3,3,5}
Symmetry	+1/5[C5×C5]	+1/8[C8×C8]		+1/12[C12×C12]	+1/30[C30×C30]
Coxeter plane symmetry	Dih5, [5], (*5•)	Dih8, [8], (*8•)		Dih12, [12], (*12•)	Dih30, [30], (*30•)
Petrie polygons of the regular 4D solids, showing 5-fold, 8-fold, 12-fold and 30-fold symmetry.

In five dimension, the symmetry of a regular polyteron, {p,q,r,s}, with one directed petrie polygon marked, is represented by the composite of 5 reflections.

Coxeter group	A5, [3,3,3,3]	B5, [4,3,3,3]		D5, [32,1,1]
Regular polyteron	{3,3,3,3}	{3,3,3,4}	{4,3,3,3}	h{4,3,3,3}
Coxeter plane symmetry	Dih6, [6], (*6•)	Dih10, [10], (*10•)		Dih8, [8], (*8•)

In dimensions 6 to 8 there are 3 exceptional Coxeter groups, one uniform polytope from each dimension represents the roots of the E_n Exceptional lie groups. The Coxeter elements are 12, 18 and 30 respectively.

E_n groups

Coxeter group	E6	E7	E8
Graph	122	231	421
Coxeter plane symmetry	Dih12, [12], (*12•)	Dih18, [18], (*18•)	Dih30, [30], (*30•)

See also

• Longest element of a Coxeter group

References

• Coxeter, H. S. M. (1948), Regular Polytopes, Methuen and Co.
• Steinberg, R. (June 1959), "Finite Reflection Groups", Transactions of the American Mathematical Society, 91 (3): 493–504, doi:10.1090/S0002-9947-1959-0106428-2, ISSN 0002-9947, JSTOR 1993261
• Hiller, Howard Geometry of Coxeter groups. Research Notes in Mathematics, 54. Pitman (Advanced Publishing Program), Boston, Mass.-London, 1982. iv+213 pp. ISBN 0-273-08517-4
• Humphreys, James E. (1992), Reflection Groups and Coxeter Groups, Cambridge University Press, pp. 74–76 (Section 3.16, Coxeter Elements), ISBN 978-0-521-43613-7
• Stembridge, John (April 9, 2007), Coxeter Planes
• Stekolshchik, R. (2008), Notes on Coxeter Transformations and the McKay Correspondence, Springer Monographs in Mathematics, doi:10.1007/978-3-540-77398-3, ISBN 978-3-540-77398-6
• Reading, Nathan (2010), "Noncrossing Partitions, Clusters and the Coxeter Plane", Séminaire Lotharingien de Combinatoire, B63b: 32