Euler's identity

The exponential function $e$ ^$z$ can be defined as the limit of (1 + $z$ / $N$ )^$N$, as $N$ approaches infinity, and thus $e$ ^{$i$ $π$} is the limit of (1 + $i$ $π$ / $N$ )^$N$. In this animation $N$ takes various increasing values from 1 to 100. The computation of (1 + $i$ $π$ / $N$ )^$N$ is displayed as the combined effect of $N$ repeated multiplications in the complex plane, with the final point being the actual value of (1 + $i$ $π$ / $N$ )^$N$. It can be seen that as $N$ gets larger (1 + $i$ $π$ / $N$ )^$N$ approaches a limit of −1.

In mathematics, Euler's identity^{[n 1]} (also known as Euler's equation) is the equality

e^{i\pi }+1=0

where

$e$ is Euler's number, the base of natural logarithms,

$i$ is the imaginary unit, which satisfies

i

² = −1, and

$π$ is pi, the ratio of the circumference of a circle to its diameter.

Euler's identity is named after the Swiss mathematician Leonhard Euler. It is considered an example of mathematical beauty.

Explanation

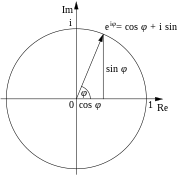
Euler's identity is a special case of Euler's formula from complex analysis, which states that for any real number $x$ ,

e^{ix}=\cos x+i\sin x\,\!

where the values of the trigonometric functions sine and cosine are given in radians.

In particular, when $x$ = $π$ , or one half-turn (180°) around a circle:

e^{i\pi }=\cos \pi +i\sin \pi .\,\!

Since

\cos \pi =-1\,\!

and

\sin \pi =0,\,\!

it follows that

e^{i\pi }=-1+0i,\,\!

which yields Euler's identity:

e^{i\pi }+1=0.\,\!

Mathematical beauty

Euler's identity is often cited as an example of deep mathematical beauty.^[3] Three of the basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants:^[4]

The number 0, the additive identity.
The number 1, the multiplicative identity.
The number $π$ , which is ubiquitous in trigonometry, the geometry of Euclidean space, and analytical mathematics ( $π$ = 3.14159265...)
The number $e$ , the base of natural logarithms, which occurs widely in mathematical, scientific and financial analysis ( $e$ = 2.718281828...). Both $π$ and e are transcendental numbers.
The number $i$ , the imaginary unit of the complex numbers, a field of numbers that contains the roots of all polynomials (that are not constants), and whose study leads to deeper insights into many areas of algebra and calculus.

Furthermore, the equation is given in the form of an expression set equal to zero, which is common practice in algebra and other areas of mathematics.

Paul Nahin, a professor emeritus at the University of New Hampshire, states in his book dedicated to Euler's identity and its applications in Fourier analysis that the formula sets "the gold standard for mathematical beauty".^[5]

After proving Euler's identity during a lecture, Benjamin Peirce, a noted American 19th-century philosopher, mathematician, and professor at Harvard University, stated that "it is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth."^[6] Stanford University mathematics professor Keith Devlin has said, "Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's equation reaches down into the very depths of existence."^[7]

The German mathematician Carl Friedrich Gauss was reported to have commented that if this formula was not immediately apparent to a student upon being told it, that student would never be a first-class mathematician.^[8]

The mathematics writer Constance Reid claimed that Euler's identity was "the most famous formula in all mathematics".^[9] A poll of readers conducted by The Mathematical Intelligencer in 1990 named Euler's identity as the "most beautiful theorem in mathematics".^[10] In another poll of readers that was conducted by Physics World in 2004, Euler's identity tied with Maxwell's equations (of electromagnetism) as the "greatest equation ever".^[11]

Generalizations

Euler's identity is also a special case of the more general identity that the nth roots of unity, for n > 1, add up to 0:

\sum _{k=0}^{n-1}e^{2\pi ik/n}=0.

Euler's identity is the case where $n$ = 2.

In another field of mathematics, by using quaternion exponentiation, one can show that a similar identity also applies to quaternions. Let {i, j, k} be the basis elements, then,

e^{{\frac {(i\pm j\pm k)}{\sqrt {3}}}\pi }+1=0.\,

In general, given real a₁, a₂, and a₃ such that ${a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}=1$ , then,

e^{(a_{1}i+a_{2}j+a_{3}k)\pi }+1=0.\,

For octonions, with real a_n such that ${a_{1}}^{2}+{a_{2}}^{2}+\dots +{a_{7}}^{2}=1$ and the octonion basis elements {i₁, i₂,..., i₇}, then,

e^{(a_{1}i_{1}+a_{2}i_{2}+\dots +a_{7}i_{7})\pi }+1=0.\,

History

It has been claimed that Euler's identity appears in his monumental work of mathematical analysis published in 1748, Introductio in analysin infinitorum.^[12] However, it is questionable whether this particular concept can be attributed to Euler himself, as he may never have expressed it.^[13] (Moreover, while Euler did write in the Introductio about what we today call "Euler's formula",^[14] which relates $e$ with cosine and sine terms in the field of complex numbers, the English mathematician Roger Cotes also knew of this formula and Euler may have acquired the knowledge through his Swiss compatriot Johann Bernoulli.^[13])

In popular culture

Euler's identity is referenced in episode 3 of series 3 of Dara Ó Briain: School of Hard Sums (2014) and at least two episodes of The Simpsons: "Treehouse of Horror VI" (1995)^[15] and "MoneyBart" (2010).^[16]

Notes and references

Notes

^ The term "Euler's identity" (or "Euler identity") is also used elsewhere to refer to other concepts, including the related general formula $e ix = cos x + i sin x$ ,^[1] and the Euler product formula.^[2]

References

^ Dunham, 1999, p. xxiv.
^ Stepanov, S.A. [originator] (7 February 2011). "Euler identity". Encyclopedia of Mathematics. Retrieved 18 February 2014.
^ Gallagher, James (13 February 2014). "Mathematics: Why the brain sees maths as beauty". BBC News online. Retrieved 13 February 2014.
^ Paulos, p. 117.
^ Cited in Crease, 2007.
^ Maor p. 160 and Kasner & Newman pp. 103–104.
^ Nahin, 2006, p. 1.
^ Derbyshire, p. 210.
^ Reid, p. 155.
^ Nahin, 2006, pp. 2–3 (poll published in the summer 1990 issue of the magazine).
^ Crease, 2004.
^ Conway and Guy, pp. 254–255.
^ ^a ^b Sandifer, p. 4.
^ Euler, p. 147.
^ Cohen, David X (2005), "Commentary for "Treehouse of Horror VI", The Simpsons: The Complete Seventh Season, 20th Century Fox.
^ Singh, Simon (22 September 2013). "The Simpsons' secret formula: it's written by maths geeks". The Guardian. Retrieved 22 September 2013.

Sources

Conway, John Horton, and Guy, Richard (1996). The Book of Numbers (Springer, 1996). ISBN 978-0-387-97993-9.
Crease, Robert P., "The greatest equations ever", PhysicsWeb, October 2004 (registration required).
Crease, Robert P. "Equations as icons," PhysicsWeb, March 2007 (registration required).
Dunham, William (1999). Euler: The Master of Us All. Mathematical Association of America. ISBN 978-0-88385-328-3.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics (New York: Penguin, 2004).
Euler, Leonhard. Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus (Leipzig: B. G. Teubneri, 1922).
Kasner, E., and Newman, J., Mathematics and the Imagination (Simon & Schuster, 1940).
Maor, Eli, e: The Story of a number (Princeton University Press, 1998). ISBN 0-691-05854-7
Nahin, Paul J., Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills (Princeton University Press, 2006). ISBN 978-0-691-11822-2
Paulos, John Allen, Beyond Numeracy: An Uncommon Dictionary of Mathematics (Penguin Books, 1992). ISBN 0-14-014574-5
Reid, Constance, From Zero to Infinity (Thomas Crowell, 1955).
Sandifer, C. Edward. Euler's Greatest Hits (Mathematical Association of America, 2007). ISBN 978-0-88385-563-8

External links

[3] The term "Euler's identity" (or "Euler identity") is also used elsewhere to refer to other concepts, including the related general formula $e ix = cos x + i sin x$ ,^[1] and the Euler product formula.^[2]

[1] Dunham, 1999, p. xxiv.

[EOM-2] Stepanov, S.A. [originator] (7 February 2011). "Euler identity". Encyclopedia of Mathematics. Retrieved 18 February 2014.

[Gallagher2014-4] Gallagher, James (13 February 2014). "Mathematics: Why the brain sees maths as beauty". BBC News online. Retrieved 13 February 2014.

[5] Paulos, p. 117.

[6] Cited in Crease, 2007.

[7] Maor p. 160 and Kasner & Newman pp. 103–104.

[8] Nahin, 2006, p. 1.

[9] Derbyshire, p. 210.

[10] Reid, p. 155.

[11] Nahin, 2006, pp. 2–3 (poll published in the summer 1990 issue of the magazine).

[12] Crease, 2004.

[13] Conway and Guy, pp. 254–255.

[Sandifer2007-14] Sandifer, p. 4.

[15] Euler, p. 147.

[16] Cohen, David X (2005), "Commentary for "Treehouse of Horror VI", The Simpsons: The Complete Seventh Season, 20th Century Fox.

[17] Singh, Simon (22 September 2013). "The Simpsons' secret formula: it's written by maths geeks". The Guardian. Retrieved 22 September 2013.

[n 1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[1]

[2]