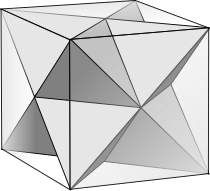
Faceting
In geometry, faceting (also spelled facetting) is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.
New edges of a faceted polyhedron may be created along face diagonals or internal space diagonals. A faceted polyhedron will have two faces on each edge and creates new polyhedra or compounds of polyhedra.
Faceting is the reciprocal or dual process to stellation. For every stellation of some convex polytope, there exists a dual faceting of the dual polytope.
Faceted polygons
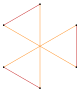
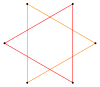
[edit]For example, a regular pentagon has one symmetry faceting, the pentagram, and the regular hexagon has two symmetric facetings, one as a polygon, and one as a compound of two triangles.
| Pentagon | Hexagon | Decagon | |||||||
|---|---|---|---|---|---|---|---|---|---|

|
|
| |||||||
| Pentagram {5/2} |
Star hexagon | Compound 2{3} |
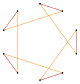
Decagram {10/3} |
Compound 2{5} |
Compound 2{5/2} |
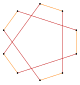
Star decagon | |||

|
|
|

|

|

|
|

|
|

|
Faceted polyhedra
[edit]The regular icosahedron can be faceted into three regular Kepler–Poinsot polyhedra: small stellated dodecahedron, great dodecahedron, and great icosahedron. They all have 30 edges.
| Convex | Regular stars | ||
|---|---|---|---|
| icosahedron | great dodecahedron | small stellated dodecahedron | great icosahedron |

|

|

|

|
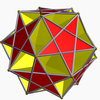
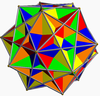
The regular dodecahedron can be faceted into one regular Kepler–Poinsot polyhedron, three uniform star polyhedra, and three regular polyhedral compound. The uniform stars and compound of five cubes are constructed by face diagonals. The excavated dodecahedron is a facetting with star hexagon faces.
| Convex | Regular compounds | ||
|---|---|---|---|
| dodecahedron | five tetrahedra | five cubes | ten tetrahedra |

|

|
|

|
History
[edit]Faceting has not been studied as extensively as stellation.
- In 1568 Wenzel Jamnitzer published his book Perspectiva Corporum Regularium, showing many stellations and facetings of polyhedra.[1]
- In 1619, Kepler described a regular compound of two tetrahedra which fits inside a cube, and which he called the Stella octangula.
- In 1858, Bertrand derived the regular star polyhedra (Kepler–Poinsot polyhedra) by faceting the regular convex icosahedron and dodecahedron.
- In 1974, Bridge enumerated the more straightforward facetings of the regular polyhedra, including those of the dodecahedron.
- In 2006, Inchbald described the basic theory of faceting diagrams for polyhedra. For a given vertex, the diagram shows all the possible edges and facets (new faces) which may be used to form facetings of the original hull. It is dual to the dual polyhedron's stellation diagram, which shows all the possible edges and vertices for some face plane of the original core.
References
[edit]Notes
[edit]- ^ Mathematical Treasure: Wenzel Jamnitzer's Platonic Solids by Frank J. Swetz (2013): "In this study of the five Platonic solids, Jamnitzer truncated, stellated, and faceted the regular solids [...]"
Bibliography
[edit]- Bertrand, J. Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46 (1858), pp. 79–82.
- Bridge, N.J. Facetting the dodecahedron, Acta crystallographica A30 (1974), pp. 548–552.
- Inchbald, G. Facetting diagrams, The mathematical gazette, 90 (2006), pp. 253–261.
- Alan Holden, Shapes, Space, and Symmetry. New York: Dover, 1991. p.94
External links
[edit]- Weisstein, Eric W. "Faceting". MathWorld.
- Olshevsky, George. "Faceting". Glossary for Hyperspace. Archived from the original on 4 February 2007.