Guyou hemisphere-in-a-square projection

    Add links
    From Wikipedia, the free encyclopedia
    Guyou doubly periodic projection of the world.
    The Guyou hemisphere-in-a-square projection with Tissot's indicatrix of deformation. The indicatrix is omitted at the singular points. At those points the deformation is infinite; the indicatrix would be infinite in size.

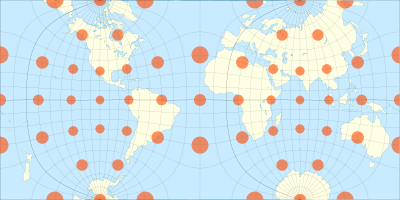
    The Guyou hemisphere-in-a-square projection is a conformal map projection for the hemisphere. It is an oblique aspect of the Peirce quincuncial projection.

    History[edit]

    The projection was developed by Émile Guyou [fr] of France in 1887.[1][2]

    Formal description[edit]

    The projection can be computed as an oblique aspect of the Peirce quincuncial projection by rotating the axis 45 degrees. It can also be computed by rotating the coordinates −45 degrees before computing the stereographic projection; this projection is then remapped into a square whose coordinates are then rotated 45 degrees.[3]

    The projection is conformal except for the four corners of each hemisphere’s square. Like other conformal polygonal projections, the Guyou is a Schwarz–Christoffel mapping.

    Properties[edit]

    Its properties are very similar to those of the Peirce quincuncial:

    • Each hemisphere is represented as a square, the sphere as a rectangle of aspect ratio 2:1.
    • The part where the exaggeration of scale amounts to double that at the centre of each square is only 9% of the area of the sphere, against 13% for the Mercator and 50% for the stereographic[4]
    • The curvature of lines representing great circles is, in every case, very slight, over the greater part of their length.[4]
    • It is conformal everywhere except at the corners of the square that corresponds to each hemisphere, where two meridians change direction abruptly twice each; the Equator is represented by a horizontal line.
    • It can be tessellated in all directions.

    Related projections[edit]

    See also[edit]

    References[edit]

    1. ^ E. Guyou (1887) "Nouveau système de projection de la sphère: Généralisation de la projection de Mercator", Annales Hydrographiques, Ser. 2, Vol. 9, 16–35. https://www.retronews.fr/journal/annales-hydrographiques/1-janvier-1887/1877/4868382/23
    2. ^ Snyder, John P. (1993). Flattening the Earth. University of Chicago. ISBN 0-226-76746-9.
    3. ^ L.P. Lee (1976). "Conformal Projections based on Elliptic Functions". Cartographica. 13 (Monograph 16, supplement No. 1 to Canadian Cartographer).
    4. ^ a b C.S. Peirce (December 1879). "A Quincuncial Projection of the Sphere". American Journal of Mathematics. The Johns Hopkins University Press. 2 (4): 394–396. doi:10.2307/2369491. JSTOR 2369491.
    Retrieved from "https://en.wikipedia.org/w/index.php?title=Guyou_hemisphere-in-a-square_projection&oldid=1072445996"