Hopf algebra

In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an (unital associative) algebra and a (counital coassociative) coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property. The representation theory of a Hopf algebra is particularly nice, since the existence of compatible comultiplication, counit, and antipode allows for the construction of tensor products of representations, trivial representations, and dual representations.

Hopf algebras occur naturally in algebraic topology, where they originated and are related to the H-space concept, in group scheme theory, in group theory (via the concept of a group ring), and in numerous other places, making them probably the most familiar type of bialgebra. Hopf algebras are also studied in their own right, with much work on specific classes of examples on the one hand and classification problems on the other.

Formal definition

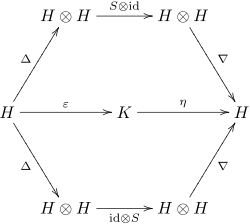
Formally, a Hopf algebra is a (associative and coassociative) bialgebra H over a field K together with a K-linear map $S\colon H\to H$ (called the antipode) such that the following diagram commutes:

Here Δ is the comultiplication of the bialgebra, ∇ its multiplication, η its unit and ε its counit. In the sumless Sweedler notation, this property can also be expressed as

$S(c_{(1)})c_{(2)}=c_{(1)}S(c_{(2)})=\epsilon (c)1\qquad {\mbox{ for all }}c\in H.$

As for algebras, one can replace the underlying field K with a commutative ring R in the above definition.

The definition of Hopf algebra is self-dual (as reflected in the symmetry of the above diagram), so if one can define a dual of H (which is always possible if H is finite-dimensional), then it is automatically a Hopf algebra.

Properties of the antipode

The antipode S is sometimes required to have a K-linear inverse, which is automatic in the finite-dimensional case, or if H is commutative or cocommutative (or more generally quasitriangular).

In general, S is an antihomomorphism, so $S^{2}$ is a homomorphism, which is therefore an automorphism if S was invertible (as may be required).

If $S^{2}=Id$, then the Hopf algebra is said to be involutive (and the underlying algebra with involution is a *-algebra). If H is finite-dimensional semisimple over a field of characteristic zero, commutative, or cocommutative, then it is involutive.

If a bialgebra B admits an antipode S, then S is unique ("a bialgebra admits at most 1 Hopf algebra structure").

The antipode is an analog to the inversion map on a group that sends $g$ to $g^{-1}$.

Hopf subalgebras

A subalgebra A of a Hopf algebra H is a Hopf subalgebra if it is a subcoalgebra of H and the antipode S maps A into A. In other words, a Hopf subalgebra A is a Hopf algebra in its own right when the multiplication, comultiplication, counit and antipode of H is restricted to A (and additionally the identity 1 of H is required to be in A). The Nichols-Zoeller Freeness theorem established (in 1989) that the natural A-module H is free of finite rank if H is finite dimensional: a generalization of Lagrange's theorem for subgroups. As a corollary of this and integral theory, a Hopf subalgebra of a semisimple finite dimensional Hopf algebra is automatically semisimple.

A Hopf subalgebra A is said to be right normal in a Hopf algebra H if it satisfies the condition of stability, $ad_{r}(h)(A)\subseteq A$ for all h in H, where the right adjoint mapping $ad_{r}$ is defined by $ad_{r}(h)(a)=S(h_{(1)})ah_{(2)}$ for all a in A, h in H. Similarly, a Hopf subalgebra A is left normal in H if it is stable under the left adjoint mapping defined by $ad_{\ell }(h)(a)=h_{(1)}aS(h_{(2)})$. The two conditions of normality are equivalent if the antipode S is bijective, in which case A is said to be a normal Hopf subalgebra.

A normal Hopf subalgebra A in H satisfies the condition (of equality of subsets of H): $HA^{+}=A^{+}H$ where $A^{+}$ denotes the kernel of the counit on K. This normality condition implies that $HA^{+}$ is a Hopf ideal of H (i.e. an algebra ideal in the kernel of the counit, a coalgebra coideal and stable under the antipode). As a consequence one has a quotient Hopf algebra $H/HA^{+}$ and epimorphism $H\rightarrow H/A^{+}H$, a theory analogous to that of normal subgroups and quotient groups in group theory.

Representation Theory

Let A be a Hopf algebra, and let $M$ and $M'$ be A-modules. Then, $M\otimes M'$ is also an A-module, with

$a(m\otimes m'):=\Delta (a)(m\otimes m')=(a_{1}\otimes a_{2})(m\otimes m')=(a_{1}m\otimes a_{2}m')$

for $m\in M$, $m'\in M'$ and $\Delta (a)=(a_{1},a_{2})$. Furthermore, we can define the trivial representation as the base field K with

$a(m):=\epsilon (a)m$

for $m\in K$. Finally, the dual representation of A can be defined: if M is an A-module and $M^{*}$ is its dual space, then

$(af)(m):=f(S(a)m)$

where $f\in M^{*}$ and $m\in M$.

The relationship between $\Delta$, $\epsilon$, and S ensure that certain natural homomorphisms of vector spaces are indeed homomorphisms of A-modules. For instance, the natural isomorphisms of vector spaces $M\to M\otimes K$ and $M\to K\otimes M$ are also isomorphisms of A-modules. Also, the map of vector spaces $M^{*}\otimes M\to K$ with $f\otimes m\to f(m)$ is also a homomorphism of A-modules. However, the map $M\otimes M^{*}\to K$ is not necessarily a homomorphism of A-modules.

Examples

1. Group algebra. Suppose G is a group. The group algebra KG is a unital associative algebra over K. It turns into a Hopf algebra if we define
   • Δ : KG → KG ⊗ KG by Δ(g) = g ⊗ g for all g in G
   • ε : KG → K by ε(g) = 1 for all g in G
   • S : KG → KG by S(g) = g ⁻¹ for all g in G.

   The Hopf algebra KG is commutative if and only if the group is commutative; it is always co-commutative (see below).

2. Functions on a finite group. Suppose now that G is a finite group. Then the set K^G of all functions from G to K with pointwise addition and multiplication is a unital associative algebra over K, and K^G ⊗ K^G is naturally isomorphic to K^GxG (for G infinite, K^G ⊗ K^G is a proper subset of K^GxG). The set K^G becomes a Hopf algebra if we define
   • Δ : K^G → K^GxG by Δ(f)(x,y) = f(xy) for all f in K^G and all x,y in G
   • ε : K^G → K by ε(f) = f(e) for every f in K^G [here e is the identity element of G]
   • S : K^G → K^G by S(f)(x) = f(x⁻¹) for all f in K^G and all x in G.

   The Hopf algebra K^G is always commutative; it is co-commutative if and only if the group is commutative.

   Note that functions on a finite group can be identified with the group ring, though these are more naturally thought of as dual – the group ring consists of finite sums of elements, and thus pairs with functions on the group by evaluating the function on the summed elements.

3. Regular functions on an algebraic group. Generalizing the previous example, we can use the same formulas to show that for a given algebraic group G over K, the set of all regular functions on G forms a Hopf algebra.
4. Tensor algebra. Suppose V is a vector space over a field K and T(V) is its tensor algebra, then T(V) becomes a Hopf algebra with
   • Δ : T(V) → T(V) ⊗ T(V) by Δ(x) = x ⊗ 1 + 1 ⊗ x for every x in T¹(V) and then linearly extend it to higher tensor power,
   • ε : T(V) → K by ε(x) = 0 for all x in Tⁿ(V)with n > 0 (and ε is the identity on K),
   • S : T(V) → T(V) by S(x) = -x for all x in T¹(V) (and extend it to higher tensor power).

   Note that the symmetric algebra and exterior algebra (which are quotients of the tensor algebra) are also Hopf algebras with this definition of the comultiplication, counit and antipode.

5. Universal enveloping algebra. Suppose g is a Lie algebra over the field K and U is its universal enveloping algebra. U becomes a Hopf algebra if we define
   • Δ : U → U ⊗ U by Δ(x) = x ⊗ 1 + 1 ⊗ x for every x in g (this rule is compatible with commutators and can therefore be uniquely extended to all of U).
   • ε : U → K by ε(x) = 0 for all x in g (again, extended to U)
   • S : U → U by S(x) = -x for all x in g.
6. Sweedler's 4-dimensional Hopf algebra. Suppose K is a field with characteristic different from 2. Let H be the K-algebra generated by c and x satisfying the relations : c² = 1, x² = 0 and xc = - cx. Then H becomes a Hopf algebra if we define
   • Δ : H → H ⊗ H by Δ (c) = c ⊗ c and Δ (x) = c ⊗ x + x ⊗ 1 (of course Δ (1) = 1 ⊗ 1)
   • ε : H → K by ε(c) = 1 and ε(x) = 0
   • S : H → H by S(c) = c^-1 = c and S(x) = -cx.

   The underlying vector space is generated by {1, c, x, cx} and thus have dimension 4. This is the smallest example of a Hopf algebra that is both non-commutative and non-cocommutative.

Cohomology of Lie groups

The cohomology algebra of a Lie group is a Hopf algebra: the multiplication is provided by the cup-product, and the comultiplication

$H^{*}(G)\rightarrow H^{*}(G\times G)\cong H^{*}(G)\otimes H^{*}(G)$

by the group multiplication $G\times G\rightarrow G$. This observation was actually a source of the notion of Hopf algebra. Using this structure, Hopf proved a structure theorem for the cohomology algebra of Lie groups.

Theorem (Hopf) Let A be a finite-dimensional, graded commutative, graded cocommutative Hopf algebra over a field of characteristic 0. Then A (as an algebra) is a free exterior algebra with generators of odd degree.

Quantum groups and non-commutative geometry

Main article: quantum group

All examples above are either commutative (i.e. the multiplication is commutative) or co-commutative (i.e. Δ = T $\circ$ Δ where T: H ⊗ H → H ⊗ H is defined by T(x ⊗ y) = y ⊗ x). Other interesting Hopf algebras are certain "deformations" or "quantizations" of those from example 3 which are neither commutative nor co-commutative. These Hopf algebras are often called quantum groups, a term that is so far only loosely defined. They are important in noncommutative geometry, the idea being the following: a standard algebraic group is well described by its standard Hopf algebra of regular functions; we can then think of the deformed version of this Hopf algebra as describing a certain "non-standard" or "quantized" algebraic group (which is not an algebraic group at all). While there does not seem to be a direct way to define or manipulate these non-standard objects, one can still work with their Hopf algebras, and indeed one identifies them with their Hopf algebras. Hence the name "quantum group".

Related concepts

Graded Hopf algebras are often used in algebraic topology: they are the natural algebraic structure on the direct sum of all homology or cohomology groups of an H-space.

Locally compact quantum groups generalize Hopf algebras and carry a topology. The algebra of all continuous functions on a Lie group is a locally compact quantum group.

Quasi-Hopf algebras are generalizations of Hopf algebras, where coassociativity only holds up to a twist.

Weak Hopf algebras, or quantum groupoids, are generalizations of Hopf algebras. Like Hopf algebras, weak Hopf algebras form a self-dual class of algebras; i.e., if H is a (weak) Hopf algebra, so is H*, the dual space of linear forms on H (with respect to the algebra-coalgebra structure obtained from the natural pairing with H and its coalgebra-algebra structure). A weak Hopf algebra H is usually taken to be a

• finite dimensional algebra and coalgebra with coproduct Δ: H → H ⊗ H and counit ε: H→ k satisfying all the axioms of Hopf algebra except possibly $\Delta (1)\neq 1\otimes 1$ or $\epsilon (ab)\neq \epsilon (a)\epsilon (b)$ for some a,b in H. Instead one requires the following:

$(\Delta (1)\otimes 1)(1\otimes \Delta (1))=(1\otimes \Delta (1))(\Delta (1)\otimes 1)=(\Delta \otimes {\mbox{Id}})\Delta (1)$

$\epsilon (abc)=\sum \epsilon (ab_{(1)})\epsilon (b_{(2)}c)=\sum \epsilon (ab_{(2)})\epsilon (b_{(1)}c)$

for all a,b, and c in H.

• H has a weakened antipode S: H → H satisfying the axioms:

(a) $S(a_{(1)})a_{(2)}=1_{(1)}\epsilon (a1_{(2)})$ for all a in H (the right-hand side is the interesting projection usually denoted by $\Pi ^{R}(a)$ or $\epsilon _{s}(a)$ with image a separable subalgebra denoted by H^R or H_s);

(b) $a_{(1)}S(a_{(2)})=\epsilon (1_{(1)}a)1_{(2)}$ for all a in H (another interesting projection usually denoted by $\Pi ^{L}(a)$ or $\epsilon _{t}(a)$ with image a separable algebra H^L or H_t, anti-isomorphic to H^L via S);

(c) $S(a_{(1)})a_{(2)}S(a_{(3)})=S(a)$ for all a in H.

Note that if Δ(1) = 1 ⊗ 1, these conditions reduce to the two usual conditions on the antipode of a Hopf algebra.

The axioms are partly chosen so that the category of H-modules is a rigid monoidal category. The unit H-module is the separable algebra H^L mentioned above.

For example, a finite groupoid algebra is a weak Hopf algebra. In particular, the groupoid algebra on [n] with one pair of invertible arrows $e_{ij}$ and $e_{ji}$ between i and j in [n] is isomorphic to the algebra H of n x n matrices. The weak Hopf algebra structure on this particular H is given by coproduct $\Delta (e_{ij})=e_{ij}\otimes e_{ij}$, counit $\epsilon (e_{ij})=1$ and antipode $S(e_{ij})=e_{ji}$. The separable subalgebras H^L and H^R coincide and are non-central commutative algebras in this particular case (the subalgebra of diagonal matrices).

Early theoretical contributions to weak Hopf algebras are to be found in as well as

Hopf algebroids introduced by J.-H. Lu in 1996 as a result on work on groupoids in Poisson geometry (later shown equivalent in nontrivial way to a construction of Takeuchi from the 1970s and another by Xu around the year 2000): Hopf algebroids generalize weak Hopf algebras and certain skew Hopf algebras. They may be loosely thought of as Hopf algebras over a noncommutative base ring, where weak Hopf algebras become Hopf algebras over a separable algebra. It is a theorem that a Hopf algebroid satisfying a finite projectivity condition over a separable algebra is a weak Hopf algebra, and conversely a weak Hopf algebra H is a Hopf algebroid over its separable subalgebra H^L. The antipode axioms have been changed by G. Böhm and K. Szlachanyi (J. Algebra) in 2004 for tensor categorical reasons and to accommodate examples associated to depth two Frobenius algebra extensions.

A left Hopf algebroid (H,R) is a left bialgebroid together with an antipode: the bialgebroid (H,R) consists of a total algebra H and a base algebra R and two mappings, an algebra homomorphism s: R → H called a source map, an algebra anti-homomorphism t: R → H called a target map, such that the commutativity condition $s(r_{1})t(r_{2})=t(r_{2})s(r_{1})$ is satisfied for all $r_{1},r_{2}\in R$. The axioms resemble those of a Hopf algebra but are complicated by the possibility that R is a noncommutative algebra or its images under s and t are not in the center of H. In particular a left bialgebroid (H,R) has an R-R-bimodule structure on H which prefers the left side as follows: $r_{1}\cdot h\cdot r_{2}=s(r_{1})t(r_{2})h$ for all h in H, $r_{1},r_{2}\in R$. There is a coproduct Δ: H → H ⊗_R H and counit ε: H → R that make (H, R, Δ, ε) an R-coring (with axioms like that of a coalgebra such that all mappings are R-R-bimodule homomorphisms and all tensors over R). Additionally the bialgebroid (H,R) must satisfy Δ(ab) = Δ(a)Δ(b) for all a,b in H, and a condition to make sure this last condition makes sense: every image point Δ(a) satisfies $a_{(1)}t(r)\otimes a_{(2)}=a_{(1)}\otimes a_{(2)}s(r)$ for all r in R. Also Δ(1) = 1 ⊗ 1. The counit is required to satisfy $\epsilon (1_{H})=1_{R}$ and the condition $\epsilon (ab)=\epsilon (as(\epsilon (b)))=\epsilon (at(\epsilon (b)))$.

The antipode S: H → H is usually taken to be an algebra anti-automorphism satisfying conditions of exchanging the source and target maps and satisfying two axioms like Hopf algebra antipode axioms; see the references in Lu or in Böhm-Szlachanyi for a more example-category friendly, though somewhat more complicated, set of axioms for the antipode S. The latter set of axioms depend on the axioms of a right bialgebroid as well, which are a straightforward switching of left to right, s with t, of the axioms for a left bialgebroid given above.

As an example of left bialgebroid, take R to be any algebra over a field k. Let H be its algebra of linear self-mappings. Let s(r) be left multication by r on R; let t(r) be right multiplication by r on R. H is a left bialgebroid over R, which may be seen as follows. From the fact that $H\otimes _{R}H\cong {\mbox{Hom}}_{k}(R\otimes R,R)$ one may define a coproduct by Δ(f)(r ⊗ u) = f(ru) for each linear transformation f from R to itself and all r,u in R. Coassociativity of the coproduct follows from associativity of the product on R. A counit is given by ε(f) = f(1). The counit axioms of a coring follow from the identity element condition on multiplication in R. The reader will be amused, or at least edified, to check that (H,R) is a left bialgebroid. In case R is an Azumaya algebra, in which case H is isomorphic to R ⊗ R, an antipode comes from transposing tensors, which makes H a Hopf algebroid over R.

Multiplier Hopf algebras introduced by Alfons Van Daele in 1994 are generalizations of Hopf algebras where comultiplication from an algebra (with or withthout unit) to the multiplier algebra of tensor product algebra of the algebra with itself.

Hopf group-(co)algebras introduced by V.G.Turaev in 2000 are also generalizations of Hopf algebras.

Analogy with groups

Groups can be axiomatized by the same diagrams (equivalently, operations) as a Hopf algebra, where G is taken to be a set instead of a module. In this case:

• the field K is replaced by the 1-point set
• there is a natural counit (map to 1 point)
• there is a natural comultiplication (the diagonal map)
• the unit is the identity element of the group
• the multiplication is the multiplication in the group
• the antipode is the inverse

In this philosophy, a group can be thought of as a Hopf algebra over the "field with one element".

See also

• Quasitriangular Hopf algebra
• Algebra/set analogy
• Representation theory of Hopf algebras
• Ribbon Hopf algebra
• Superalgebra
• Supergroup
• Anyonic Lie algebra
• Sweedler's Hopf algebra

References

• Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras, Pure and Applied Mathematics, vol. 235 (1st ed.), Marcel Dekker, ISBN 0-8247-0481-9 {{citation}}: Unknown parameter |subtitle= ignored (help).
• Pierre Cartier, A primer of Hopf algebras, IHES preprint, September 2006, 81 pages
• Jurgen Fuchs, Affine Lie Algebras and Quantum Groups, (1992), Cambridge University Press. ISBN 0-521-48412-X
• H. Hopf, Uber die Topologie der Gruppen-Mannigfaltigkeiten und ihrer Verallgemeinerungen, Ann. of Math. 42 (1941), 22-52. Reprinted in Selecta Heinz Hopf, pp. 119–151, Springer, Berlin (1964). MR4784
• Street, Ross (2007), Quantum groups, Australian Mathematical Society Lecture Series, vol. 19, Cambridge University Press, ISBN 978-0-521-69524-4; 978-0-521-69524-4, MR2294803 {{citation}}: Check |isbn= value: invalid character (help).
• Sweedler, Moss E. (1969), Hopf algebras, Mathematics Lecture Note Series, W. A. Benjamin, Inc., New York, MR 0252485