Inversion (discrete mathematics)
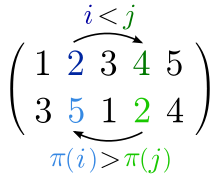
In computer science and discrete mathematics, an inversion in a sequence is a pair of elements that are out of their natural order.
Definitions[edit]
Inversion[edit]
Let be a permutation. There is an inversion of between and if and . The inversion is indicated by an ordered pair containing either the places [1][2] or the elements .[3][4][5]
The inversion set is the set of all inversions. A permutation's inversion set using place-based notation is the same as the inverse permutation's inversion set using element-based notation with the two components of each ordered pair exchanged. Likewise, a permutation's inversion set using element-based notation is the same as the inverse permutation's inversion set using place-based notation with the two components of each ordered pair exchanged.[6]
Inversions are usually defined for permutations, but may also be defined for sequences:
Let be a sequence (or multiset permutation[7]). If and , either the pair of places [7][8] or the pair of elements [9] is called an inversion of .
For sequences, inversions according to the element-based definition are not unique, because different pairs of places may have the same pair of values.
Inversion number[edit]
The inversion number [10] of a sequence , is the cardinality of the inversion set. It is a common measure of sortedness (sometimes called presortedness) of a permutation[5] or sequence.[9] The inversion number is between 0 and inclusive. A permutation and its inverse have the same inversion number.
For example since the sequence is ordered. Also, when is even, (because each pair is an inversion). This last example shows that a set that is intuitively "nearly sorted" can still have a quadratic number of inversions.
The inversion number is the number of crossings in the arrow diagram of the permutation,[6] the permutation's Kendall tau distance from the identity permutation, and the sum of each of the inversion related vectors defined below.
Other measures of sortedness include the minimum number of elements that can be deleted from the sequence to yield a fully sorted sequence, the number and lengths of sorted "runs" within the sequence, the Spearman footrule (sum of distances of each element from its sorted position), and the smallest number of exchanges needed to sort the sequence.[11] Standard comparison sorting algorithms can be adapted to compute the inversion number in time O(n log n).[12]
[edit]
Three similar vectors are in use that condense the inversions of a permutation into a vector that uniquely determines it. They are often called inversion vector or Lehmer code. (A list of sources is found here.)
This article uses the term inversion vector () like Wolfram.[13] The remaining two vectors are sometimes called left and right inversion vector, but to avoid confusion with the inversion vector this article calls them left inversion count () and right inversion count (). Interpreted as a factorial number the left inversion count gives the permutations reverse colexicographic,[14] and the right inversion count gives the lexicographic index.

Inversion vector :
With the element-based definition is the number of inversions whose smaller (right) component is .[3]
- is the number of elements in greater than before .
Left inversion count :
With the place-based definition is the number of inversions whose bigger (right) component is .
- is the number of elements in greater than before .
Right inversion count , often called Lehmer code:
With the place-based definition is the number of inversions whose smaller (left) component is .
- is the number of elements in smaller than after .
Both and can be found with the help of a Rothe diagram, which is a permutation matrix with the 1s represented by dots, and an inversion (often represented by a cross) in every position that has a dot to the right and below it. is the sum of inversions in row of the Rothe diagram, while is the sum of inversions in column . The permutation matrix of the inverse is the transpose, therefore of a permutation is of its inverse, and vice versa.
Example: All permutations of four elements[edit]

The following sortable table shows the 24 permutations of four elements (in the column) with their place-based inversion sets (in the p-b column), inversion related vectors (in the , , and columns), and inversion numbers (in the # column). (The columns with smaller print and no heading are reflections of the columns next to them, and can be used to sort them in colexicographic order.)
It can be seen that and always have the same digits, and that and are both related to the place-based inversion set. The nontrivial elements of are the sums of the descending diagonals of the shown triangle, and those of are the sums of the ascending diagonals. (Pairs in descending diagonals have the right components 2, 3, 4 in common, while pairs in ascending diagonals have the left components 1, 2, 3 in common.)
The default order of the table is reverse colex order by , which is the same as colex order by . Lex order by is the same as lex order by .
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Weak order of permutations[edit]

The set of permutations on n items can be given the structure of a partial order, called the weak order of permutations, which forms a lattice.
The Hasse diagram of the inversion sets ordered by the subset relation forms the skeleton of a permutohedron.
If a permutation is assigned to each inversion set using the place-based definition, the resulting order of permutations is that of the permutohedron, where an edge corresponds to the swapping of two elements with consecutive values. This is the weak order of permutations. The identity is its minimum, and the permutation formed by reversing the identity is its maximum.
If a permutation were assigned to each inversion set using the element-based definition, the resulting order of permutations would be that of a Cayley graph, where an edge corresponds to the swapping of two elements on consecutive places. This Cayley graph of the symmetric group is similar to its permutohedron, but with each permutation replaced by its inverse.
See also[edit]
- Factorial number system
- Permutation graph
- Transpositions, simple transpositions, inversions and sorting
- Damerau–Levenshtein distance
- Parity of a permutation
Sequences in the OEIS:
- Sequences related to factorial base representation
- Factorial numbers: A007623 and A108731
- Inversion numbers: A034968
- Inversion sets of finite permutations interpreted as binary numbers: A211362 (related permutation: A211363)
- Finite permutations that have only 0s and 1s in their inversion vectors: A059590 (their inversion sets: A211364)
- Number of permutations of n elements with k inversions; Mahonian numbers: A008302 (their row maxima; Kendall-Mann numbers: A000140)
- Number of connected labeled graphs with n edges and n nodes: A057500
References[edit]
- ^ Aigner 2007, pp. 27.
- ^ Comtet 1974, pp. 237.
- ^ a b Knuth 1973, pp. 11.
- ^ Pemmaraju & Skiena 2003, pp. 69.
- ^ a b Vitter & Flajolet 1990, pp. 459.
- ^ a b Gratzer 2016, pp. 221.
- ^ a b Bóna 2012, pp. 57.
- ^ Cormen et al. 2001, pp. 39.
- ^ a b Barth & Mutzel 2004, pp. 183.
- ^ Mannila 1985.
- ^ Mahmoud 2000, pp. 284.
- ^ Kleinberg & Tardos 2005, pp. 225.
- ^ Weisstein, Eric W. "Inversion Vector" From MathWorld--A Wolfram Web Resource
- ^ Reverse colex order of finitary permutations (sequence A055089 in the OEIS)
Source bibliography[edit]
- Aigner, Martin (2007). "Word Representation". A course in enumeration. Berlin, New York: Springer. ISBN 978-3642072536.
- Barth, Wilhelm; Mutzel, Petra (2004). "Simple and Efficient Bilayer Cross Counting". Journal of Graph Algorithms and Applications. 8 (2): 179–194. doi:10.7155/jgaa.00088.
- Bóna, Miklós (2012). "2.2 Inversions in Permutations of Multisets". Combinatorics of permutations. Boca Raton, FL: CRC Press. ISBN 978-1439850510.
- Comtet, Louis (1974). "6.4 Inversions of a permutation of [n]". Advanced combinatorics; the art of finite and infinite expansions. Dordrecht, Boston: D. Reidel Pub. Co. ISBN 9027704414.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. ISBN 0-262-53196-8.
- Gratzer, George (2016). "7-2 Basic objects". Lattice theory. special topics and applications. Cham, Switzerland: Birkhäuser. ISBN 978-3319442358.
- Kleinberg, Jon; Tardos, Éva (2005). Algorithm Design. ISBN 0-321-29535-8.
- Knuth, Donald (1973). "5.1.1 Inversions". The Art of Computer Programming. Addison-Wesley Pub. Co. ISBN 0201896850.
- Mahmoud, Hosam Mahmoud (2000). "Sorting Nonrandom Data". Sorting: a distribution theory. Wiley-Interscience series in discrete mathematics and optimization. Vol. 54. Wiley-IEEE. ISBN 978-0-471-32710-3.
- Pemmaraju, Sriram V.; Skiena, Steven S. (2003). "Permutations and combinations". Computational discrete mathematics: combinatorics and graph theory with Mathematica. Cambridge University Press. ISBN 978-0-521-80686-2.
- Vitter, J.S.; Flajolet, Ph. (1990). "Average-Case Analysis of Algorithms and Data Structures". In van Leeuwen, Jan (ed.). Algorithms and Complexity. Vol. 1 (2nd ed.). Elsevier. ISBN 978-0-444-88071-0.
Further reading[edit]
- Margolius, Barbara H. (2001). "Permutations with Inversions". Journal of Integer Sequences. 4.
Presortedness measures[edit]
- Mannila, Heikki (April 1985). "Measures of presortedness and optimal sorting algorithms". IEEE Transactions on Computers. C-34 (4): 318–325. doi:10.1109/tc.1985.5009382.
- Estivill-Castro, Vladimir; Wood, Derick (1989). "A new measure of presortedness". Information and Computation. 83 (1): 111–119. doi:10.1016/0890-5401(89)90050-3.
- Skiena, Steven S. (1988). "Encroaching lists as a measure of presortedness". BIT. 28 (4): 755–784. doi:10.1007/bf01954897. S2CID 33967672.



























