Kalah
| Kalah | |
|---|---|
 | |
| Ranks | Two |
| Sowing | Single lap |
| Region | United States, United Kingdom |
Kalah is a modern variation in the ancient Mancala family of games. The Kalah board was first patented and sold in the United States by William Julius Champion, Jr. in the 1950s.[1][2] This game is sometimes also called "Kalahari", possibly by false etymology from the Kalahari desert in Namibia.[citation needed]
For most of its variations, Kalah is a solved game with a first-player win if both players play perfect games. The pie rule can be used to balance the first-player's advantage.
Standard gameplay
[edit]The game provides a Kalah board and a number of seeds or counters. The board has 6 small pits, called houses, on each side; and a big pit, called an end zone or store, at each end. The object of the game is to capture more seeds than one's opponent.
- At the beginning of the game, four seeds are placed in each house. This is the traditional method.
- Each player controls the six houses and their seeds on the player's side of the board. The player's score is the number of seeds in the store to their right.
- Players take turns sowing their seeds. On a turn, the player removes all seeds from one of the houses under their control. Moving counter-clockwise, the player drops one seed in each house in turn, including the player's own store but not their opponent's.
- If the last sown seed lands in an empty house owned by the player, and the opposite house contains seeds, both the last seed and the opposite seeds are captured and placed into the player's store.
- If the last sown seed lands in the player's store, the player gets an additional move. There is no limit on the number of moves a player can make in their turn.
- When one player no longer has any seeds in any of their houses, the game ends. The other player moves all remaining seeds to their store, and the player with the most seeds in their store wins.
It is possible for the game to end in a draw.
Example turn
[edit]The player begins sowing from the highlighted house.
The last seed falls in the store, so the player receives an extra move.
The last seed falls in an empty house on the player's side. The player collects the highlighted seeds from both their own house and the opposite house of their opponent and will move them to the store.
Video game implementation
[edit]Kalah was implemented on the PDP-1 in the early 1960s,[3] and was able to out-play experienced human players.[4] Since then, there have been myriad Kalah implementations for various operating systems and platforms, including DOS,[5] and the Nokia 3310.[6]
Variations
[edit]- The game may start with a number of seeds in each house different from four. A nomenclature has been developed to describe these variations: Kalah(h,s), where h designates the number of houses on each side, and s designates the number of seeds that start out in each house. In broad terms, the more seeds, the more challenging is the game. The three-, four-, five- and six-seed Kalah have been solved, with the starting player always winning with perfect play.[7][8] Thus some web sites have implemented the game with the pie rule to make it fair, or the second player may be allowed to move one seed from any house to any other house before the game begins, resulting in effectively 144 different games.
- An alternative rule has players sow in a clockwise direction, requiring more stones to be sowed in a single turn to reach the store.
- The "Empty Capture" variant: If the last sown seed lands in an empty house owned by the player, even if the opposite house is empty, the last seed is captured and placed into the player's store.
- In the "Seed On" variant, there is no captures when ending in an empty house, but when the last seed ends in a non-empty house on either side of the board, that seed and all seeds from that house are sown, so that the move only ends when the last seed falls in an empty house.
- Alternative rules either count the remaining seeds at the end of the game as part of the score of the player who has emptied their houses, or do not count them at all.
Mathematical analysis
[edit]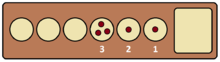
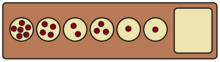
As mentioned above, if the last seed sown by a player lands in that player's store, the player gets an extra move. A clever player can take advantage of this rule to chain together many extra turns. Certain configurations of a row of the board can in this way be cleared in a single turn, that is, the player can capture all stones on their row, as depicted on the right. The longest possible such chain on a standard Kalah board of 6 pits lasts for 17 moves. On a general n-pit board, the patterns of seeds which can be cleared in a single turn in this way have been the object of mathematical study.[9] One can prove that, for all n, there exists one and only one pattern clearable in exactly n moves, or equivalently, one and only one clearable pattern consisting of exactly n seeds.
These patterns require arbitrarily long rows of pits and n increases. For example, it can be seen on the right that the unique 5-seed pattern requires only 3 pits, but the 17-seed pattern requires 6 pits. The relationship between the required number of pits and the number of seeds can be described in the following way. Let s(n) denote the minimum number of seeds which requires n pits to clear. Then where the symbol denotes asymptotic equivalence, that is, , or equivalently, .[9]
See also
[edit]References
[edit]- ^ "Kalah: A Commercial Count and Capture Game". University of Waterloo. Archived from the original on 5 Feb 2024. Retrieved May 27, 2024.
- ^ US Expired 2720362A, William J Champion, "Game Counter", published 1955-10-11
- ^ PDP Application Note: Kalah. Digital Equipment Computer Users Society (DECUS). 31 March 1961. Retrieved May 28, 2024.
- ^ "Games: Pits & Pebbles". TIME. June 14, 1963. Retrieved May 28, 2024.
{{cite magazine}}: CS1 maint: url-status (link) - ^ https://archive.org/details/Kalakh "Kalakh" videogame on archive.org, with in-browser DOS emulation gameplay
- ^ Nokia 3310 gameplay of "Bantumi", a kalah-identical game
- ^ Solving Kalah by Geoffrey Irving, Jeroen Donkers and Jos Uiterwijk.
- ^ Solving (6,6)-Kalaha by Anders Carstensen.
- ^ a b Broline, Duane M.; Loeb, Daniel E. (1995-02-08). "The combinatorics of Mancala-type games: Ayo, Tchoukaitlon, and 1/π". arXiv:math/9502225.




