Matched Z-transform method


The matched Z-transform method, also called the pole–zero mapping[1][2] or pole–zero matching method,[3] and abbreviated MPZ or MZT,[4] is a technique for converting a continuous-time filter design to a discrete-time filter (digital filter) design.
The method works by mapping all poles and zeros of the s-plane design to z-plane locations , for a sample interval .[5] So an analog filter with transfer function:
is transformed into the digital transfer function
The gain must be adjusted to normalize the desired gain, typically set to match the analog filter's gain at DC by setting and and solving for .[3][6]
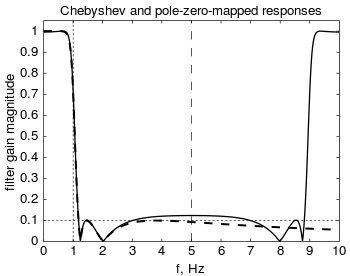
Since the mapping wraps the s-plane's axis around the z-plane's unit circle repeatedly, any zeros (or poles) greater than the Nyquist frequency will be mapped to an aliased location.[7]
In the (common) case that the analog transfer function has more poles than zeros, the zeros at may optionally be shifted down to the Nyquist frequency by putting them at , causing the transfer function to drop off as in much the same manner as with the bilinear transform (BLT).[1][3][6][7]
While this transform preserves stability and minimum phase, it preserves neither time- nor frequency-domain response and so is not widely used.[8][7] More common methods include the BLT and impulse invariance methods.[4] MZT does provide less high frequency response error than the BLT, however, making it easier to correct by adding additional zeros, which is called the MZTi (for "improved").[9]
A specific application of the matched Z-transform method in the digital control field is with the Ackermann's formula, which changes the poles of the controllable system; in general from an unstable (or nearby) location to a stable location.
References[edit]
- ^ a b Won Young Yang (2009). Signals and Systems with MATLAB. Springer. p. 292. ISBN 978-3-540-92953-6.
- ^ Bong Wie (1998). Space vehicle dynamics and control. AIAA. p. 151. ISBN 978-1-56347-261-9.
- ^ a b c Arthur G. O. Mutambara (1999). Design and analysis of control systems. CRC Press. p. 652. ISBN 978-0-8493-1898-6.
- ^ a b Al-Alaoui, M. A. (February 2007). "Novel Approach to Analog-to-Digital Transforms". IEEE Transactions on Circuits and Systems I: Regular Papers. 54 (2): 338–350. doi:10.1109/tcsi.2006.885982. ISSN 1549-8328. S2CID 9049852.
- ^ S. V. Narasimhan and S. Veena (2005). Signal processing: principles and implementation. Alpha Science Int'l Ltd. p. 260. ISBN 978-1-84265-199-5.
- ^ a b Franklin, Gene F. (2015). Feedback control of dynamic systems. Powell, J. David, Emami-Naeini, Abbas (Seventh ed.). Boston: Pearson. pp. 607–611. ISBN 978-0133496598. OCLC 869825370.
Because physical systems often have more poles than zeros, it is useful to arbitrarily add zeros at z = -1.
- ^ a b c Rabiner, Lawrence R; Gold, Bernard (1975). Theory and application of digital signal processing. Englewood Cliffs, New Jersey: Prentice-Hall. pp. 224–226. ISBN 0139141014.
The expediency of artificially adding zeros at z = —1 to the digital system has been suggested ... but this ad hoc technique is at best only a stopgap measure. ... In general, use of impulse invariant or bilinear transformation is to be preferred over the matched z transformation.
- ^ Jackson, Leland B. (1996). Digital Filters and Signal Processing. Springer Science & Business Media. p. 262. ISBN 9780792395591.
although perfectly usable filters can be designed in this way, no special time- or frequency-domain properties are preserved by this transformation, and it is not widely used.
- ^ Ojas, Chauhan; David, Gunness (2007-09-01). "Optimizing the Magnitude Response of Matched Z-Transform Filters ("MZTi") for Loudspeaker Equalization". Audio Engineering Society. Archived from the original on July 27, 2019. Alt URL











