Multitrait-multimethod matrix
The multitrait-multimethod (MTMM) matrix is an approach to examining construct validity developed by Campbell and Fiske (1959).[1] It organizes convergent and discriminant validity evidence for comparison of how a measure relates to other measures. The conceptual approach has influenced experimental design and measurement theory in psychology, including applications in structural equation models.
| Part of a series on |
| Psychology |
|---|
Definitions and key components
[edit]Multiple traits are used in this approach to examine (a) similar or (b) dissimilar traits (constructs), in order to establish convergent and discriminant validity between traits. Similarly, multiple methods are used in this approach to examine the differential effects (or lack thereof) caused by method specific variance. Scores could be correlated because they measure similar traits, or because they are based on similar methods, or both. When variables that are supposed to measure different constructs show a high correlation because they based on similar methods, this is sometimes described as a "nuisance variance" or "method bias" problem.[2]
There are six major considerations when examining a construct's validity through the MTMM matrix, which are as follows:
- Evaluation of convergent validity – Tests designed to measure the same construct should correlate highly amongst themselves.
- Evaluation of discriminant (divergent) validity – The construct being measured by a test should not correlate highly with different constructs.
- Trait-method unit- Each task or test used in measuring a construct is considered a trait-method unit; in that the variance contained in the measure is part trait, and part method. Generally, researchers desire low method-specific variance and high trait variance.
- Multitrait-multimethod – More than one trait and more than one method must be used to establish (a) discriminant validity and (b) the relative contributions of the trait or method-specific variance. This tenet is consistent with the ideas proposed in Platt's concept of Strong inference (1964).[3]
- Truly different methodology – When using multiple methods, one must consider how different the actual measures are. For instance, delivering two self-report measures are not truly different measures; whereas using an interview scale or a psychosomatic reading would be.
- Trait characteristics – Traits should be different enough to be distinct, but similar enough to be worth examining in the MTMM.
Example
[edit]The example below provides a prototypical matrix and what the correlations between measures mean. The diagonal line is typically filled in with a reliability coefficient of the measure (e.g. alpha coefficient). Descriptions in brackets [] indicate what is expected when the validity of the construct (e.g., depression or anxiety) and the validities of the measures are all high.
| Test | Beck Depression Inventory (BDI) - Questionnaire | Hamilton Depression Rating Scale (HDRS) - Interview | Beck Anxiety Inventory (BAI) - Questionnaire | Clinician Global Impressions - Anxiety (CGI-A) - Interview |
|---|---|---|---|---|
| BDI | (Reliability Coefficient)
[close to 1.00] |
|||
| HDRS | Heteromethod-monotrait
[highest of all except reliability] |
(Reliability Coefficient)
[close to 1.00] |
||
| BAI | Monomethod-heterotrait
[low, less than monotrait] |
Heteromethod-heterotrait
[lowest of all] |
(Reliability Coefficient) [close to 1.00] | |
| CGI-A | Heteromethod-heterotrait
[lowest of all] |
Monomethod-heterotrait
[low, less than monotrait] |
Heteromethod-monotrait
[highest of all except reliability] |
(Reliability Coefficient)
[close to 1.00] |
In this example, the first row lists the trait being assessed (i.e., depression or anxiety) as well as the method of assessing this trait (i.e., self-reported questionnaire versus an interview). The term heteromethod indicates this cell reports the correlation between two separate methods. Monomethod indicates that the same method is being used instead (e.g., interview and interview). Heterotrait indicates that the cell refers to two supposedly different traits. Monotrait indicates the same trait supposed to be measured.
This framework makes it clear that there are at least two sources of variance that can influence observed scores on a measure: Not just the underlying trait (which is usually the goal of gathering the measurement in the first place), but also the method used to gather the measurement. The MTMM matrix uses two or more measures of each trait and two or more methods to start to tease apart the contributions of different factors. The first frame of the animated figure shows how the four measurements in the table are paired in terms of focusing on the "traits" of depression (BDI and HDRS) and anxiety (BAI and CGI-A). The second shows that they are also paired in terms of source method: two use self-report questionnaires (often referred to as "surveys"), and two are based on interview (which can incorporate direct observation of nonverbal communication and behavior, as well as the interviewee's response).
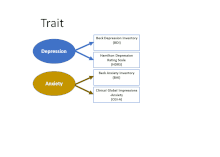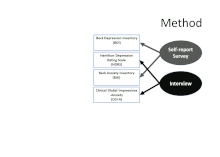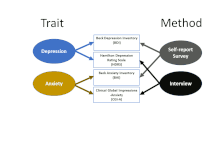
With observed data, it is possible to examine the proportion of variance shared among traits and methods to gain a sense of how much method-specific variance is induced by the measurement method, as well as provide a look at how distinct the trait is, as compared to another trait.
Ideally, the trait should matter more than the specific method chosen for measurement. For example, if a person is measured as being highly depressed by one measure, then another depression measure should also yield high scores. On the other hand, people who appear highly depressed on the Beck Depression Inventory should not necessarily get high anxiety scores on Beck's Anxiety Inventory, inasmuch as they are supposed to be measuring different constructs. Since the inventories were written by the same person, and are similar in style, there might be some correlation, but this similarity in method should not affect the scores much, so the correlations between these measures of different traits should be low.
Analysis
[edit]A variety of statistical approaches have been used to analyze the data from the MTMM matrix. The standard method from Campbell and Fiske can be implemented using the MTMM.EXE program available at: https://web.archive.org/web/20160304173400/http://gim.med.ucla.edu/FacultyPages/Hays/utils/ One can also use confirmatory factor analysis[4] due to the complexities in considering all of the data in the matrix. The Sawilowsky I test,[5][6] however, considers all of the data in the matrix with a distribution-free statistical test for trend.

The test is conducted by reducing the heterotrait-heteromethod and heterotrait-monomethod triangles, and the validity and reliability diagonals, into a matrix of four levels. Each level consists of the minimum, median, and maximum value. The null hypothesis is these values are unordered, which is tested against the alternative hypothesis of an increasing ordered trend. The test statistic is found by counting the number of inversions (I). The critical value for alpha = 0.05 is 10, and for alpha = .01 is 14.
One of the most used models to analyze MTMM data is the True Score model proposed by Saris and Andrews ([7]).
The True Score model can be expressed using the following standardized equations:
1) Yij = rij TSij + eij* where: Yij is the standardized observed variable measured with the ith trait and jth method. rij is the reliability coefficient, which is equal to: rij = σYij / σTSij TSij is the standardized true score variable eij* is the random error, which is equal to: eij* = eij / σYij Consequently: rij2 = 1 - σ2 (eij*) where: rij2 is the reliability
2) TSij = vij Fi + mij Mj where: vij is the validity coefficient, which is equal to: vij = σFi / σTSij Fi is the standardized latent factor for the ith variable of interest (or trait) mij is the method effect, which is equal to: mij = σMj / σTSij Mj is the standardized latent factor for the reaction to the jthmethod Consequently: vij2 = 1 - mij2 where: vij2 is the validity
3) Yij = qijFi + rijmijMj + e* where: qij is the quality coefficient, which is equal to: qij = rij • vij Consequently: qij2 = rij2 • vij2 = σ2Fi / σ2Yij where: qij2 is the quality
The assumptions are the following:
* The errors are random, thus the mean of the errors is zero: µe = E(e) = 0 * The random errors are uncorrelated with each other: cov(ei, ej) = E(ei ej) = 0 * The random errors are uncorrelated with the independent variables: cov(TS, e) = E(TS e) = 0 , cov(F, e) = E(F e) = 0 and cov(M, e) = E(M e) = 0 * The method factors are assumed to be uncorrelated with one another and with the trait factors: cov(F, M) = E(F M) = 0
Typically, the respondent must answer at least three different measures (i.e., traits) measured using at least three different methods.
This model has been used to estimate the quality of thousands of survey questions, in particular in the frame of the European Social Survey.
References
[edit]- ^ Campbell, D.T., & FiskeD.W. (1959) Convergent and discriminant validation by the multitrait-multimethod matrix. Psychological Bulletin, 56, 81-105 "
- ^ Podsakoff, Philip M.; MacKenzie, Scott B.; Podsakoff, Nathan P. (2012-01-10). "Sources of Method Bias in Social Science Research and Recommendations on How to Control It". Annual Review of Psychology. 63 (1): 539–569. doi:10.1146/annurev-psych-120710-100452. ISSN 0066-4308.
- ^ John R. Platt (1964). "Strong inference". Science 146 (3642).
- ^ Figueredo, A., Ferketich, S., Knapp, T. (1991). Focus on psychometrics: More on MTMM: The Role of Confirmatory Factor Analysis. Nursing & Health, 14, 387-391
- ^ Sawilowsky, S. (2002). A quick distribution-free test for trend that contributes evidence of construct validity. Measurement and Evaluation in Counseling and Development, 35, 78-88.
- ^ Cuzzocrea, J., & Sawilowsky, S. (2009). Robustness to non-independence and power of the I test for trend in construct validity. Journal of Modern Applied Statistical Methods, 8(1), 215-225.
- ^ Saris, W. E. and Andrews, F. M. (1991). Evaluation of measurement instruments using a Structural Modeling Approach. Pp. 575 – 599 in Measurement errors in surveys, edited by Biemer, P. P. et al. New York: Wiley.
