Operad
In mathematics, an operad is a structure that consists of abstract operations, each one having a fixed finite number of inputs (arguments) and one output, as well as a specification of how to compose these operations. Given an operad , one defines an algebra over to be a set together with concrete operations on this set which behave just like the abstract operations of . For instance, there is a Lie operad such that the algebras over are precisely the Lie algebras; in a sense abstractly encodes the operations that are common to all Lie algebras. An operad is to its algebras as a group is to its group representations.
History
[edit]Operads originate in algebraic topology; they were introduced to characterize iterated loop spaces by J. Michael Boardman and Rainer M. Vogt in 1968[1][2] and by J. Peter May in 1972.[3]
Martin Markl, Steve Shnider, and Jim Stasheff write in their book on operads:[4]
- "The name operad and the formal definition appear first in the early 1970's in J. Peter May's "The Geometry of Iterated Loop Spaces", but a year or more earlier, Boardman and Vogt described the same concept under the name categories of operators in standard form, inspired by PROPs and PACTs of Adams and Mac Lane. In fact, there is an abundance of prehistory. Weibel [Wei] points out that the concept first arose a century ago in A.N. Whitehead's "A Treatise on Universal Algebra", published in 1898."
The word "operad" was created by May as a portmanteau of "operations" and "monad" (and also because his mother was an opera singer).[5]
Interest in operads was considerably renewed in the early 90s when, based on early insights of Maxim Kontsevich, Victor Ginzburg and Mikhail Kapranov discovered that some duality phenomena in rational homotopy theory could be explained using Koszul duality of operads.[6][7] Operads have since found many applications, such as in deformation quantization of Poisson manifolds, the Deligne conjecture,[8] or graph homology in the work of Maxim Kontsevich and Thomas Willwacher.
Intuition
[edit]Suppose is a set and for we define
- ,
the set of all functions from the cartesian product of copies of to .
We can compose these functions: given , , the function
is defined as follows: given arguments from , we divide them into blocks, the first one having arguments, the second one arguments, etc., and then apply to the first block, to the second block, etc. We then apply to the list of values obtained from in such a way.
We can also permute arguments, i.e. we have a right action of the symmetric group on , defined by
for , and .
The definition of a symmetric operad given below captures the essential properties of these two operations and .
Definition
[edit]Non-symmetric operad
[edit]A non-symmetric operad (sometimes called an operad without permutations, or a non- or plain operad) consists of the following:
- a sequence of sets, whose elements are called -ary operations,
- an element in called the identity,
- for all positive integers , , a composition function
satisfying the following coherence axioms:
- identity:
- associativity:
Symmetric operad
[edit]A symmetric operad (often just called operad) is a non-symmetric operad as above, together with a right action of the symmetric group on for , denoted by and satisfying
- equivariance: given a permutation ,
- (where on the right hand side refers to the element of that acts on the set by breaking it into blocks, the first of size , the second of size , through the th block of size , and then permutes these blocks by , keeping each block intact)
- and given permutations ,
- (where denotes the element of that permutes the first of these blocks by , the second by , etc., and keeps their overall order intact).
The permutation actions in this definition are vital to most applications, including the original application to loop spaces.
Morphisms
[edit]A morphism of operads consists of a sequence
that:
- preserves the identity:
- preserves composition: for every n-ary operation and operations ,
- preserves the permutation actions: .
Operads therefore form a category denoted by .
In other categories
[edit]So far operads have only been considered in the category of sets. More generally, it is possible to define operads in any symmetric monoidal category C . In that case, each is an object of C, the composition is a morphism in C (where denotes the tensor product of the monoidal category), and the actions of the symmetric group elements are given by isomorphisms in C.
A common example is the category of topological spaces and continuous maps, with the monoidal product given by the cartesian product. In this case, a topological operad is given by a sequence of spaces (instead of sets) . The structure maps of the operad (the composition and the actions of the symmetric groups) are then assumed to be continuous. The result is called a topological operad. Similarly, in the definition of a morphism of operads, it would be necessary to assume that the maps involved are continuous.
Other common settings to define operads include, for example, modules over a commutative ring, chain complexes, groupoids (or even the category of categories itself), coalgebras, etc.
Algebraist definition
[edit]Given a commutative ring R we consider the category of modules over R. An operad over R can be defined as a monoid object in the monoidal category of endofunctors on (it is a monad) satisfying some finiteness condition.[note 1]
For example, a monoid object in the category of "polynomial endofunctors" on is an operad.[8] Similarly, a symmetric operad can be defined as a monoid object in the category of -objects, where means a symmetric group.[9] A monoid object in the category of combinatorial species is an operad in finite sets.
An operad in the above sense is sometimes thought of as a generalized ring. For example, Nikolai Durov defines his generalized rings as monoid objects in the monoidal category of endofunctors on that commute with filtered colimits.[10] This is a generalization of a ring since each ordinary ring R defines a monad that sends a set X to the underlying set of the free R-module generated by X.
Understanding the axioms
[edit]Associativity axiom
[edit]"Associativity" means that composition of operations is associative (the function is associative), analogous to the axiom in category theory that ; it does not mean that the operations themselves are associative as operations. Compare with the associative operad, below.
Associativity in operad theory means that expressions can be written involving operations without ambiguity from the omitted compositions, just as associativity for operations allows products to be written without ambiguity from the omitted parentheses.
For instance, if is a binary operation, which is written as or . So that may or may not be associative.
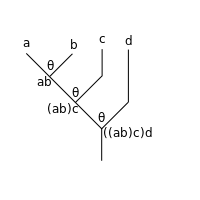
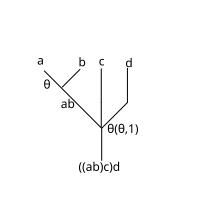
Then what is commonly written is unambiguously written operadically as . This sends to (apply on the first two, and the identity on the third), and then the on the left "multiplies" by . This is clearer when depicted as a tree:
which yields a 3-ary operation:
However, the expression is a priori ambiguous: it could mean , if the inner compositions are performed first, or it could mean , if the outer compositions are performed first (operations are read from right to left). Writing , this is versus . That is, the tree is missing "vertical parentheses":
If the top two rows of operations are composed first (puts an upward parenthesis at the line; does the inner composition first), the following results:
which then evaluates unambiguously to yield a 4-ary operation. As an annotated expression:
If the bottom two rows of operations are composed first (puts a downward parenthesis at the line; does the outer composition first), following results:
which then evaluates unambiguously to yield a 4-ary operation:
The operad axiom of associativity is that these yield the same result, and thus that the expression is unambiguous.
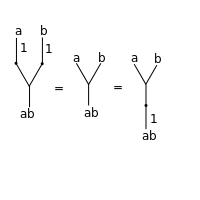
Identity axiom
[edit]The identity axiom (for a binary operation) can be visualized in a tree as:
meaning that the three operations obtained are equal: pre- or post- composing with the identity makes no difference. As for categories, is a corollary of the identity axiom.
Examples
[edit]Endomorphism operad in sets and operad algebras
[edit]The most basic operads are the ones given in the section on "Intuition", above. For any set , we obtain the endomorphism operad consisting of all functions . These operads are important because they serve to define operad algebras. If is an operad, an operad algebra over is given by a set and an operad morphism . Intuitively, such a morphism turns each "abstract" operation of into a "concrete" -ary operation on the set . An operad algebra over thus consists of a set together with concrete operations on that follow the rules abstractely specified by the operad .
Endomorphism operad in vector spaces and operad algebras
[edit]If k is a field, we can consider the category of finite-dimensional vector spaces over k; this becomes a monoidal category using the ordinary tensor product over k. We can then define endomorphism operads in this category, as follows. Let V be a finite-dimensional vector space The endomorphism operad of V consists of[11]
- = the space of linear maps ,
- (composition) given , , ..., , their composition is given by the map ,
- (identity) The identity element in is the identity map ,
- (symmetric group action) operates on by permuting the components of the tensors in .
If is an operad, a k-linear operad algebra over is given by a finite-dimensional vector space V over k and an operad morphism ; this amounts to specifying concrete multilinear operations on V that behave like the operations of . (Notice the analogy between operads&operad algebras and rings&modules: a module over a ring R is given by an abelian group M together with a ring homomorphism .)
Depending on applications, variations of the above are possible: for example, in algebraic topology, instead of vector spaces and tensor products between them, one uses (reasonable) topological spaces and cartesian products between them.
"Little something" operads
[edit]
The little 2-disks operad is a topological operad where consists of ordered lists of n disjoint disks inside the unit disk of centered at the origin. The symmetric group acts on such configurations by permuting the list of little disks. The operadic composition for little disks is illustrated in the accompanying figure to the right, where an element is composed with an element to yield the element obtained by shrinking the configuration of and inserting it into the i-th disk of , for .
Analogously, one can define the little n-disks operad by considering configurations of disjoint n-balls inside the unit ball of .[12]
Originally the little n-cubes operad or the little intervals operad (initially called little n-cubes PROPs) was defined by Michael Boardman and Rainer Vogt in a similar way, in terms of configurations of disjoint axis-aligned n-dimensional hypercubes (n-dimensional intervals) inside the unit hypercube.[13] Later it was generalized by May[14] to the little convex bodies operad, and "little disks" is a case of "folklore" derived from the "little convex bodies".[15]
Rooted trees
[edit]In graph theory, rooted trees form a natural operad. Here, is the set of all rooted trees with n leaves, where the leaves are numbered from 1 to n. The group operates on this set by permuting the leaf labels. Operadic composition is given by replacing the i-th leaf of by the root of the i-th tree , for , thus attaching the n trees to and forming a larger tree, whose root is taken to be the same as the root of and whose leaves are numbered in order.
Swiss-cheese operad
[edit]
The Swiss-cheese operad is a two-colored topological operad defined in terms of configurations of disjoint n-dimensional disks inside a unit n-semidisk and n-dimensional semidisks, centered at the base of the unit semidisk and sitting inside of it. The operadic composition comes from gluing configurations of "little" disks inside the unit disk into the "little" disks in another unit semidisk and configurations of "little" disks and semidisks inside the unit semidisk into the other unit semidisk.
The Swiss-cheese operad was defined by Alexander A. Voronov.[16] It was used by Maxim Kontsevich to formulate a Swiss-cheese version of Deligne's conjecture on Hochschild cohomology.[17] Kontsevich's conjecture was proven partly by Po Hu, Igor Kriz, and Alexander A. Voronov[18] and then fully by Justin Thomas.[19]
Associative operad
[edit]Another class of examples of operads are those capturing the structures of algebraic structures, such as associative algebras, commutative algebras and Lie algebras. Each of these can be exhibited as a finitely presented operad, in each of these three generated by binary operations.
For example, the associative operad is a symmetric operad generated by a binary operation , subject only to the condition that
This condition corresponds to associativity of the binary operation ; writing multiplicatively, the above condition is . This associativity of the operation should not be confused with associativity of composition which holds in any operad; see the axiom of associativity, above.
In the associative operad, each is given by the symmetric group , on which acts by right multiplication. The composite permutes its inputs in blocks according to , and within blocks according to the appropriate .
The algebras over the associative operad are precisely the semigroups: sets together with a single binary associative operation. The k-linear algebras over the associative operad are precisely the associative k-algebras.
Terminal symmetric operad
[edit]The terminal symmetric operad is the operad which has a single n-ary operation for each n, with each acting trivially. The algebras over this operad are the commutative semigroups; the k-linear algebras are the commutative associative k-algebras.
Operads from the braid groups
[edit]Similarly, there is a non- operad for which each is given by the Artin braid group . Moreover, this non- operad has the structure of a braided operad, which generalizes the notion of an operad from symmetric to braid groups.
Linear algebra
[edit]In linear algebra, real vector spaces can be considered to be algebras over the operad of all linear combinations [citation needed]. This operad is defined by for , with the obvious action of permuting components, and composition given by the concatentation of the vectors , where . The vector for instance represents the operation of forming a linear combination with coefficients 2,3,-5,0,...
This point of view formalizes the notion that linear combinations are the most general sort of operation on a vector space – saying that a vector space is an algebra over the operad of linear combinations is precisely the statement that all possible algebraic operations in a vector space are linear combinations. The basic operations of vector addition and scalar multiplication are a generating set for the operad of all linear combinations, while the linear combinations operad canonically encodes all possible operations on a vector space.
Similarly, affine combinations, conical combinations, and convex combinations can be considered to correspond to the sub-operads where the terms of the vector sum to 1, the terms are all non-negative, or both, respectively. Graphically, these are the infinite affine hyperplane, the infinite hyper-octant, and the infinite simplex. This formalizes what is meant by being or the standard simplex being model spaces, and such observations as that every bounded convex polytope is the image of a simplex. Here suboperads correspond to more restricted operations and thus more general theories.
Commutative-ring operad and Lie operad
[edit]The commutative-ring operad is an operad whose algebras are the commutative rings. It is defined by , with the obvious action of and operadic composition given by substituting polynomials (with renumbered variables) for variables. A similar operad can be defined whose algebras are the associative, commutative algebras over some fixed base field. The Koszul-dual of this operad is the Lie operad (whose algebras are the Lie algebras), and vice versa.
Free Operads
[edit]Typical algebraic constructions (e.g., free algebra construction) can be extended to operads. Let denote the category whose objects are sets on which the group acts. Then there is a forgetful functor , which simply forgets the operadic composition. It is possible to construct a left adjoint to this forgetful functor (this is the usual definition of free functor). Given a collection of operations E, is the free operad on E.
Like a group or a ring, the free construction allows to express an operad in terms of generators and relations. By a free representation of an operad , we mean writing as a quotient of a free operad where E describes generators of and the kernel of the epimorphism describes the relations.
A (symmetric) operad is called quadratic if it has a free presentation such that is the generator and the relation is contained in .[20]
Clones
[edit]Clones are the special case of operads that are also closed under identifying arguments together ("reusing" some data). Clones can be equivalently defined as operads that are also a minion (or clonoid).
Operads in homotopy theory
[edit]This section needs expansion. You can help by adding to it. (December 2018) |
In Stasheff (2004), Stasheff writes:
- Operads are particularly important and useful in categories with a good notion of "homotopy", where they play a key role in organizing hierarchies of higher homotopies.
See also
[edit]- PRO (category theory)
- Algebra over an operad
- Higher-order operad
- E∞-operad
- Pseudoalgebra
- Multicategory
Notes
[edit]- ^ ”finiteness" refers to the fact that only a finite number of inputs are allowed in the definition of an operad. For example, the condition is satisfied if one can write
- ,
- .
Citations
[edit]- ^ Boardman, J. M.; Vogt, R. M. (1 November 1968). "Homotopy-everything $H$-spaces". Bulletin of the American Mathematical Society. 74 (6): 1117–1123. doi:10.1090/S0002-9904-1968-12070-1. ISSN 0002-9904.
- ^ Boardman, J. M.; Vogt, R. M. (1973). Homotopy Invariant Algebraic Structures on Topological Spaces. Lecture Notes in Mathematics. Vol. 347. doi:10.1007/bfb0068547. ISBN 978-3-540-06479-4. ISSN 0075-8434.
- ^ May, J. P. (1972). The Geometry of Iterated Loop Spaces. Lecture Notes in Mathematics. Vol. 271. CiteSeerX 10.1.1.146.3172. doi:10.1007/bfb0067491. ISBN 978-3-540-05904-2. ISSN 0075-8434.
- ^ "Operads in Algebra, Topology and Physics": Martin Markl, Steve Shnider, Jim Stasheff, Mathematical Surveys and Monographs, Volume: 96; 2002
- ^ May, J. Peter. "Operads, Algebras, and Modules" (PDF). math.uchicago.edu. p. 2. Retrieved 28 September 2018.
- ^ Ginzburg, Victor; Kapranov, Mikhail (1994). "Koszul duality for operads". Duke Mathematical Journal. 76 (1): 203–272. doi:10.1215/S0012-7094-94-07608-4. ISSN 0012-7094. MR 1301191. S2CID 115166937. Zbl 0855.18006 – via Project Euclid.
- ^ Loday, Jean-Louis (1996). "La renaissance des opérades". www.numdam.org. Séminaire Nicolas Bourbaki. MR 1423619. Zbl 0866.18007. Retrieved 27 September 2018.
- ^ a b Kontsevich, Maxim; Soibelman, Yan (26 January 2000). "Deformations of algebras over operads and Deligne's conjecture". arXiv:math/0001151.
- ^ Jones, J. D. S.; Getzler, Ezra (8 March 1994). "Operads, homotopy algebra and iterated integrals for double loop spaces". arXiv:hep-th/9403055.
- ^ N. Durov, New approach to Arakelov geometry, University of Bonn, PhD thesis, 2007; arXiv:0704.2030.
- ^ Markl, Martin (2006). "Operads and PROPs". Handbook of Algebra. 5 (1): 87–140. arXiv:math/0601129. doi:10.1016/S1570-7954(07)05002-4. ISBN 9780444531018. S2CID 3239126. Example 2
- ^ Giovanni Giachetta, Luigi Mangiarotti, Gennadi Sardanashvily (2005) Geometric and Algebraic Topological Methods in Quantum Mechanics, ISBN 981-256-129-3, pp. 474,475
- ^ Greenlees, J. P. C. (2002). Axiomatic, Enriched and Motivic Homotopy Theory. Proceedings of the NATO Advanced Study Institute on Axiomatic, Enriched and Motivic Homotopy Theory. Cambridge, United Kingdom: Springer Science & Business Media. pp. 154–156. ISBN 978-1-4020-1834-3.
- ^ May, J. P. (1977). "Infinite loop space theory". Bull. Amer. Math. Soc. 83 (4): 456–494. doi:10.1090/s0002-9904-1977-14318-8.
- ^ Stasheff, Jim (1998). "Grafting Boardman's Cherry Trees to Quantum Field Theory". arXiv:math/9803156.
- ^ Voronov, Alexander A. (1999). The Swiss-cheese operad. Contemporary Mathematics. Baltimore, Maryland, United States: AMS. pp. 365–373. ISBN 978-0-8218-7829-3.
- ^ Kontsevich, Maxim (1999). "Operads and Motives in Deformation Quantization". Lett. Math. Phys. 48: 35–72. arXiv:math/9904055. Bibcode:1999math......4055K. doi:10.1023/A:1007555725247. S2CID 16838440.
- ^ Hu, Po; Kriz, Igor; Voronov, Alexander A. (2006). "On Kontsevich's Hochschild cohomology conjecture". Compositio Mathematica. 142 (1): 143–168. arXiv:math/0309369. doi:10.1112/S0010437X05001521.
- ^ Thomas, Justin (2016). "Kontsevich's Swiss cheese conjecture". Geom. Topol. 20 (1): 1–48. arXiv:1011.1635. doi:10.2140/gt.2016.20.1. S2CID 119320246.
- ^ Markl, Martin (2006). "Operads and PROPs". Handbook of Algebra. 5: 87–140. doi:10.1016/S1570-7954(07)05002-4. ISBN 9780444531018. S2CID 3239126. Definition 37
References
[edit]- Tom Leinster (2004). Higher Operads, Higher Categories. Cambridge University Press. arXiv:math/0305049. Bibcode:2004hohc.book.....L. ISBN 978-0-521-53215-0.
- Martin Markl, Steve Shnider, Jim Stasheff (2002). Operads in Algebra, Topology and Physics. American Mathematical Society. ISBN 978-0-8218-4362-8.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Markl, Martin (June 2006). "Operads and PROPs". arXiv:math/0601129.
- Stasheff, Jim (June–July 2004). "What Is...an Operad?" (PDF). Notices of the American Mathematical Society. 51 (6): 630–631. Retrieved 17 January 2008.
- Loday, Jean-Louis; Vallette, Bruno (2012), Algebraic Operads (PDF), Grundlehren der Mathematischen Wissenschaften, vol. 346, Berlin, New York: Springer-Verlag, ISBN 978-3-642-30361-6
- Zinbiel, Guillaume W. (2012), "Encyclopedia of types of algebras 2010", in Bai, Chengming; Guo, Li; Loday, Jean-Louis (eds.), Operads and universal algebra, Nankai Series in Pure, Applied Mathematics and Theoretical Physics, vol. 9, pp. 217–298, arXiv:1101.0267, Bibcode:2011arXiv1101.0267Z, ISBN 9789814365116
- Fresse, Benoit (17 May 2017), Homotopy of Operads and Grothendieck-Teichmüller Groups, Mathematical Surveys and Monographs, American Mathematical Society, ISBN 978-1-4704-3480-9, MR 3643404, Zbl 1373.55014
- Miguel A. Mendéz (2015). Set Operads in Combinatorics and Computer Science. SpringerBriefs in Mathematics. ISBN 978-3-319-11712-6.
- Samuele Giraudo (2018). Nonsymmetric Operads in Combinatorics. Springer International Publishing. ISBN 978-3-030-02073-6.































































































































![{\displaystyle P(n)=\mathbb {Z} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0ed04ca845c8706d66e50e0752596f443f10894)










