Petersen graph

Petersen graph
The Petersen graph is most commonly drawn as a pentagon with a pentagram inside, with five spokes.
Named after	Julius Petersen
Vertices	10
Edges	15
Radius	2
Diameter	2
Girth	5
Automorphisms	120 (S5)
Chromatic number	3
Chromatic index	4
Fractional chromatic index	3
Properties	Cubic Strongly regular Distance-transitive Snark
Table of graphs and parameters

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring. Although the graph is generally credited to Petersen, it had in fact first appeared 12 years earlier, in 1886.

Donald Knuth states that the Petersen graph is "a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general."

Constructions

The Petersen graph is the complement of the line graph of $K_{5}$. It is also the Kneser graph $KG_{5,2}$; this means that you can form the Petersen graph by constructing a vertex for each 2-element subset of a 5-element set, and connecting two vertices by an edge if the corresponding 2-element subsets are disjoint from each other.

Geometrically, the Petersen graph is the graph formed by the vertices and edges of the hemi-dodecahedron, that is, a dodecahedron with opposite points, lines and faces identified together.

Embeddings

The Petersen graph is nonplanar. Any nonplanar graph has as minors either the complete graph $K_{5}$, or the complete bipartite graph $K_{3,3}$, but the Petersen graph has both as minors. The $K_{5}$ minor can be formed by contracting the edges of a perfect matching, for instance the five short edges in the first picture. The $K_{3,3}$ minor can be formed by deleting one vertex (for instance the central vertex of the 3-symmetric drawing) and contracting an edge incident to each neighbor of the deleted vertex.

The Petersen graph has crossing number 2.

The most common and symmetric plane drawing of the Petersen graph, as a pentagram within a pentagon, has five crossings. However, this is not the best drawing for minimizing crossings; there exists another drawing (shown in the figure) with only two crossings. Thus, the Petersen graph has crossing number 2. On a torus the Petersen graph can be drawn without edge crossings; it therefore has orientable genus 1.

The Petersen graph is a unit distance graph: it can be drawn in the plane with each edge having unit length.

The Petersen graph can also be drawn (with crossings) in the plane in such a way that all the edges have equal length. That is, it is a unit distance graph.

The simplest non-orientable surface on which the Petersen graph can be embedded without crossings is the projective plane. This is the embedding given by the hemi-dodecahedron construction of the Petersen graph. The projective plane embedding can also be formed from the standard pentagonal drawing of the Petersen graph by placing a cross-cap within the five-point star at the center of the drawing, and routing the star edges through this cross-cap; the resulting drawing has six pentagonal faces. This construction shows that the Petersen graph has non-orientable genus 1.

Symmetries

The Petersen graph is strongly regular. It is also symmetric, meaning that it is edge transitive and vertex transitive. It is one of only 13 cubic distance-regular graphs.

The automorphism group of the Petersen graph is the symmetric group $S_{5}$; the action of $S_{5}$ on the Petersen graph follows from its construction as a Kneser graph. Every homomorphism of the Petersen graph to itself that doesn't identify adjacent vertices is an automorphism. As shown in the figures, the drawings of the Petersen graph may exhibit five-way or three-way symmetry, but it is not possible to draw the Petersen graph in the plane in such a way that the drawing exhibits the full symmetry group of the graph.

Despite its high degree of symmetry, the Petersen graph is not a Cayley graph. It is the smallest vertex-transitive graph that is not a Cayley graph.

Hamiltonian paths and cycles

The Petersen graph is hypo-Hamiltonian: by deleting any vertex, such as the center vertex in the drawing, the remaining graph is Hamiltonian. In addition, this drawing shows symmetry of order three, in contrast to the symmetry of order five visible in the first drawing above.

The Petersen graph has a Hamiltonian path but no Hamiltonian cycle. It is the smallest bridgeless cubic graph with no Hamiltonian cycle. It is hypohamiltonian, meaning that although it has no Hamiltonian cycle, deleting any vertex makes it Hamiltonian, and is the smallest hypohamiltonian graph.

As a finite connected vertex-transitive graph whose don't contains a Hamiltonian cycle, the Petersen graph is a counterexample to a variant of the Lovász conjecture, but the canonical formulation of the conjecture asks for an Hamiltonian path and is verified by the Petersen graph.

Only five vertex-transitive graphs with no Hamiltonian cycles are known: the complete graph K₂, the Petersen graph, the Coxeter graph and two graphs derived from the Petersen and Coxeter graphs by replacing each vertex with a triangle. If G is a 2-connected, r-regular graph with at most 3r + 1 vertices, then G is Hamiltonian or G is the Petersen graph.

To see that the Petersen graph has no Hamiltonian cycle C, we describe the ten-vertex 3-regular graphs that do have a Hamiltonian cycle and show that none of them is the Petersen graph, by finding a cycle in each of them that is shorter than any cycle in the Petersen graph. Any ten-vertex Hamiltonian 3-regular graph consists of a ten-vertex cycle C plus five chords. If any chord connects two vertices at distance two or three along C from each other, the graph has a 3-cycle or 4-cycle, and therefore cannot be the Petersen graph. If two chords connect opposite vertices of C to vertices at distance four along C, there is again a 4-cycle. The only remaining case is a Möbius ladder formed by connecting each pair of opposite vertices by a chord, which again has a 4-cycle. Since the Petersen graph has girth five, it cannot be formed in this way and has no Hamiltonian cycle.

Coloring

A 4-coloring of the Petersen graph's edges

A 3-coloring of the Petersen graph's vertices

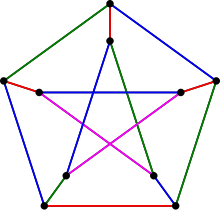
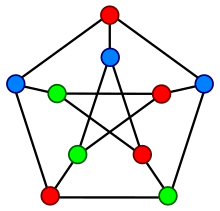
The Petersen graph has chromatic number 3, meaning that its vertices can be colored with three colors — but not with two — such that no edge connects vertices of the same color.

The Petersen graph has chromatic index 4; coloring the edges requires four colors. A proof of this requires checking four cases to demonstrate that no 3-edge-coloring exists. As a connected bridgeless cubic graph with chromatic index four, the Petersen graph is a snark. It is the smallest possible snark, and was the only known snark from 1898 until 1946. The snark theorem, a result conjectured by W. T. Tutte and announced in 2001 by Robertson, Sanders, Seymour, and Thomas, states that every snark has the Petersen graph as a minor.

Additionally, the graph has fractional chromatic index 3, proving that the difference between the chromatic index and fractional chromatic index can be as large as 1. The long-standing Goldberg-Seymour Conjecture proposes that this is the largest gap possible.

The Thue number (a variant of the chromatic index) of the Petersen graph is 5.

Other properties

The Petersen graph:

• is 3-connected and hence 3-edge-connected and bridgeless. See the glossary.
• has independence number 4 and is 3-partite. See the glossary.
• is cubic, has domination number 3, and has a perfect matching and a 2-factor. See the glossary.
• has radius 2 and diameter 2. It is the largest cubic graph with diameter 2.
• has graph spectrum −2, −2, −2, −2, 1, 1, 1, 1, 1, 3.
• is the smallest cubic graph of girth 5. (It is the unique $(3,5)$-cage. In fact, since it has only 10 vertices, it is the unique $(3,5)$-Moore graph.)
• has 2000 spanning trees, the most of any 10-vertex cubic graph.
• has chromatic polynomial $t(t-1)(t-2)(t^{7}-12t^{6}+67t^{5}-230t^{4}+529t^{3}-814t^{2}+775t-352).$
• has characteristic polynomial $(t-1)^{5}(t+2)^{4}(t-3)$, making it an integral graph—a graph whose spectrum consists entirely of integers.

Generalized Petersen graphs

In 1950 H. S. M. Coxeter introduced a family of graphs generalizing the Petersen graph. These graphs are now called generalized Petersen graphs, a name given to them in 1969 by Mark Watkins. In Watkins' notation, G(n,k) is a graph with vertex set

{u₀, u₁, ..., u_n−1, v₀, v₁, ..., v_n−1}

and edge set

{u_i u_i+1, u_i v_i, v_i v_i+k: i = 0,...,n − 1}

where subscripts are to be read modulo n and k < n/2. Coxeter's notation for the same graph would be {n}+{n/k}.

The Petersen graph itself is G(5,2) or {5}+{5/2}.

This family of graphs possesses a number of interesting properties. For example,

1. G(n,k) is vertex-transitive if and only if n = 10 and k =2 or if k² ≡ ±1 (mod n).
2. It is edge-transitive only in the following seven cases: (n,k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), (24,5). These seven graphs are therefore the only symmetric generalized Petersen graphs.
3. It is bipartite if and only if n is even and k is odd.
4. It is a Cayley graph if and only if k² ≡ 1 (mod n).
5. It is hypohamiltonian when n is congruent to 5 modulo 6 and k is 2, n−2, (n+1)/2, or (n−1)/2 (all four of these choice of k lead to isomorphic graphs). It is also non-Hamiltonian when n is divisible by four, at least equal to 8, and k is n/2. In all other cases it has a Hamiltonian cycle (Alspach 1983).

Among the generalized Petersen graphs are the n-prism $G(n,1)$, the Dürer graph $G(6,2)$, the Möbius-Kantor graph $G(8,3)$, the dodecahedron $G(10,2)$, the Desargues graph $G(10,3)$ and the Nauru graph $G(12,5)$.

The Petersen graph itself is the only generalized Petersen graph that is not 3-edge-colorable (Castagna & Prins 1972).

Petersen family

The Petersen family consists of the seven graphs that can be formed from the Petersen graph by zero or more applications of Δ-Y or Y-Δ transforms. $K_{6}$ is in the Petersen family. A graph is intrinsically linked in three dimensional real space if and only if it contains one of these graphs as a minor.

References

• Alspach, B. R. (1983), "The classification of Hamiltonian generalized Petersen graphs", Journal of Combinatorial Theory, Series B, 34: 293–312, doi:10.1016/0095-8956(83)90042-4, MR0714452.
• Castagna, Frank; Prins, Geert (1972), "Every Generalized Petersen Graph has a Tait Coloring", Pacific Journal of Mathematics, 40.
• Exoo, Geoffrey; Harary, Frank; Kabell, Jerald (1981), "The crossing numbers of some generalized Petersen graphs", Mathematica Scandinavica, 48: 184–188.
• Coxeter, H. S. M. (1950), "Self-dual configurations and regular graphs", Bulletin of the American Mathematical Society, 56: 413–455, doi:10.1090/S0002-9904-1950-09407-5.
• Frucht, R.; Graver, J. E.; Watkins, M. E. (1971), "The groups of the generalized Petersen graphs", Proceedings of the Cambridge Philosophical Society, 70: 211–218, doi:10.1017/S0305004100049811.
• Holton, D. A.; Sheehan, J. (1993), The Petersen Graph, Cambridge University Press, doi:10.2277/0521435943, ISBN 0-521-43594-3.
• Jakobson, Dmitry; Rivin, Igor (1999), On some extremal problems in graph theory, arXiv:math.CO/9907050.
• Keller, Mitch. "Kneser graphs". PlanetMath.
• Lovász, László (1993), Combinatorial Problems and Exercises (2nd ed.), North-Holland, ISBN 0-444-81504-X.
• Petersen, Julius (1898), "Sur le théorème de Tait", L'Intermédiaire des Mathématiciens, 5: 225–227.
• Valdes, L. (1991), "Extremal properties of spanning trees in cubic graphs", Congressus Numerantium, 85: 143–160.
• Watkins, Mark E. (1969), "A Theorem on Tait Colorings with an Application to the Generalized Petersen Graphs", Journal of Combinatorial Theory, 6: 152–164, doi:10.1016/S0021-9800(69)80116-X.
• Weisstein, Eric W. "Petersen Graph". MathWorld.