Petrie polygon

In geometry, a Petrie polygon is a skew polygon such that every two consecutive sides (but no three) belong to a face of a regular polyhedron.

This definition extends to higher regular polytopes. A Petrie polygon for an n-polytope is a skew polygon such that every (n-1) consecutive sides (but no n) belong to a facet of a regular polytope.

The construction of a Petrie polygon is done via an orthogonal projection onto a plane in such a way that one Petrie polygon becomes a regular polygon with the remainder of the projection interior to it. These polygons and projected graphs are useful in visualizing symmetric structure of the higher dimensional regular polytopes.

A Petrie polygon of a regular polygon {p} trivially has p sides as itself.

History

John Flinders Petrie was the only son of Sir W. M. Flinders Petrie, the great Egyptologist. He was born in 1907 and as a schoolboy showed remarkable promise of mathematical ability. In periods of intense concentration he could answer questions about complicated four-dimensional objects by visualizing them.

He first realized the importance of the regular skew polygons which appear on the surface of regular polyhedra and higher polytopes. He was a lifelong friend of Coxeter, who named these polygons after him.

The idea of Petrie polygons was later extended to semiregular polytopes.

In 1972, a few months after his retirement, Petrie was killed by a car while attempting to cross a motorway near his home in Surrey.

The Petrie polygons of the regular polyhedra

The Petrie polygon of the regular polyhedron {p, q} has h sides, where

cos²(π/h) = cos²(π/p) + cos²(π/q)

The regular duals, {p,q} and {q,p}, are contained within the same projected Petrie polygon.

Petrie polygons for regular polyhedra (red polygons)

tetrahedron	cube	octahedron	dodecahedron	icosahedron
edge-centered	vertex-centered	face-centered	face-centered	vertex-centered
4 sides	6 sides	6 sides	10 sides	10 sides
V:(4,0)	V:(6,2)	V:(6,0)	V:(10,10,0)	V:(10,2)
The Petrie polygons are the exterior of these orthogonal projections. Blue show "front" edges, while black lines show back edges. The concentric rings of vertices are counted starting from the outside working inwards with a notation: V:(a, b, ...), ending in zero if there are no central vertices.

The Petrie polygon of regular polychora (4-polytopes)

The Petrie polygon for the regular polychora {p, q ,r} can also be determined.

{3,3,3} 5-cell 5 sides V:(5,0)	{3,3,4} 16-cell 8 sides V:(8,0)	{4,3,3} tesseract 8 sides V:(8,8,0)
{3,4,3} 24-cell 12 sides V:(12,6,6,0)	{5,3,3} 120-cell 30 sides V:((30,60)3,603,30,60,0)	{3,3,5} 600-cell 30 sides V:(30,30,30,30,0)

The Petrie polygon of higher dimensional regular polytope families

The Petrie polygon for the regular polytope {p, q ,r ,..., w} can also be determined.

The simplex family

In general the n-simplex family, {3ⁿ⁻¹}, are projected into regular (n + 1)-gons with all vertices on the boundary:

n = 1 {} 1-simplex 2 sides V:(2,0)	n = 2 {3} triangle (2-simplex) 3 sides V:(3,0)	n = 3 {3,3} tetrahedron (3-simplex) 4 sides V:(4,0)
n = 4 {33} 5-cell 5 sides V:(5,0)	n = 5 {34} 5-simplex 6 sides V:(6,0)	n = 6 {35} 6-simplex 7 sides V:(7,0)
n = 7 {36} 7-simplex 8 sides V:(8,0)	n = 8 {37} 8-simplex 9 sides V:(9,0)	n = 9 {38} 9-simplex 10 sides V:(10,0)
n = 10 {39} 10-simplex 11 sides V:(11,0)	n {3n−1} n + 1 sides

The hypercube and orthoplex families

And the n-orthoplex family, {3ⁿ⁻², 4}, are projected into regular 2n-gons with all vertices on the boundary. All vertices are connected by edges except opposite ones.

n = 1 {} 2 sides V:(2,0)	n = 2 {4} square 4 sides V:(4,0)	n = 3 {3,4} octahedron 6 sides V:(6,0)
n = 4 {32,4} 16-cell 8 sides V:(8,0)	n = 5 {33,4} pentacross 10 sides V:(10,0)	n = 6 {34,4} hexacross 12 sides V:(12,0)
n = 7 {35,4} heptacross 14 sides V:(14,0)	n = 8 {36,4} octacross 16 sides V:(16,0)	n = 9 {37,4} enneacross 18 sides V:(18,0)
n = 10 {38,4} decacross 20 sides V:(20,0)	n {3n−2,4} 2n sides

And the n-hypercube family, {4, 3ⁿ⁻²}, are also projected into regular 2n-gons:

n = 1 {} 2 sides V:(2,0)	n=2 {4} square 4 sides V:(4,0)	n = 3 {4,3} cube 6 sides V:(6,2)
n = 4 {4,32} tesseract 8 sides V:(8,8,0)	n = 5 {4,33} penteract 10 sides V:(10,10,10,2)	n = 6 {4,34} hexeract 12 sides
n = 7 {4,35 hepteract 14 sides	n = 8 File:Octeract Hasse diagram.svg {4,36} octeract 16 sides	n = 9 {4,37} enneract 18 sides
n = 10 {4,38} 10-cube 20 sides	n {4,3n−2} 2n sides

Petrie polygons for semiregular polytopes

The Petrie polygon for the semiregular polytope of the form {3^p,q,r} can also be determined.

Here are two families of semiregular polytopes with regular Petrie polygons:

The demihypercube family

The n-demihypercube family, h{4, 3ⁿ⁻²} = {3^1,n−3,1}, has 2(n−1) sides. The projected vertices are identicall positioned as the (n-1)-hypercube graphs above.

n = 2 h{4}={2} digon 2 sides V:(2,0)	n = 3 h{4,3}={31,1,0}={3,3}, 110 tetrahedron 4 sides V:(4,0)	n = 4 h{4,3,3}={31,1,1}={3,3,4}, 111 16-cell 6 sides V:(6,2)
n = 5 h{4,33}={31,2,1}={32,1,1}, 121 demipenteract 8 sides V:(8,8,0)	n = 6 h{4,34}={31,3,1}, 131 demihexeract 10 sides	n = 7 h{4,35}={31,4,1}, 141 demihepteract 12 sides
n = 8 h{4,36}={31,5,1}, 151 demiocteract 14 sides	n = 9 h{4,37}={31,6,1}, 161 demienneract 16 sides	n = 10 h{4,38}={31,7,1}, 171 10-demicube 18 sides
n h{4, 3n−2}={31,n-3,1} 2(n − 1) sides

The semiregular E-polytope family

The semiregular k₂₁ polytopes E5-E8, {3^n−3,2,1}, k₂₁

n = 5 {31,2,1}, 121 E5:demipenteract 8 sides V:(8,8,0)

n = 6 {32,2,1}, 221 Gosset 2 21 polytope 12 sides V:(12,12,3)

n = 7 {33,2,1}, 321 Gosset 3 21 polytope 18 sides V:(18,18,18,2)

n = 8 {34,2,1}, 421 Gosset 4 21 polytope 30 sides V:(30,30,30,30,30,30,30,30,0)

The single-ringed uniform polytopes, {3^2,n−3,1}, 2_k1:

n = 5 {32,1,1}, 211 Pentacross 8 sides V:(8,2)

n = 6 {32,2,1}, 221 Gosset 2 21 polytope 12 sides V:(12,12,3)

n = 7 {32,3,1}, 231 Gosset 2 31 polytope 18 sides

n = 8 (No image) {32,4,1}, 241 Gosset 2 41 polytope 30 sides

The single-ringed uniform polytopes, {3^1,n−3,2}, 1_k2:

n = 5 {31,1,2}, 112 Demipenteract 8 sides (V:8,8,0)

n = 6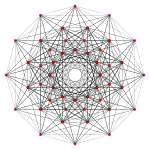 {31,2,2}, 122 Gosset 1 22 polytope 12 sides V:(12,24,12,24,0)

n = 7 (No image) {31,3,2}, 132 Gosset 1 32 polytope 18 sides

n = 8 (No image) {31,4,2}, 142 Gosset 1 42 polytope 30 sides

References

• Peter McMullen, Egon Schulte, Abstract Regular Polytopes, Cambridge University Press, 2002. ISBN 0-521-81496-0
• Coxeter, H. S. M. The Beauty of Geometry: Twelve Essays (1999), Dover Publications ISBN 99-35678
• Coxeter, H.S.M.; Regular complex polytopes (1974). Section 4.3 Flags and Orthoschemes, Section 11.3 Petrie polygons
• Coxeter, H. S. M. Petrie Polygons. Regular Polytopes, 3rd ed. New York: Dover, 1973. (sec 2.6 Petrie Polygons pp. 24–25, and Chapter 12, pp. 213-235, The generalized Petrie polygon )
• Kaleidoscopes: Selected Writings of H. S. M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (p 31 (24-cell), p 36, p 161 (definition))
• Coxeter, H.S.M.; Regular complex polytopes (1974).
• Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, 1987. (p. 135)

External links

• Weisstein, Eric W. "Petrie polygon". MathWorld.
• Weisstein, Eric W. "Hypercube graphs". MathWorld.
• Weisstein, Eric W. "Cross polytope graphs". MathWorld.
• Weisstein, Eric W. "24-cell graph". MathWorld.
• Weisstein, Eric W. "120-cell graph". MathWorld.
• Weisstein, Eric W. "600-cell graph". MathWorld.
• Weisstein, Eric W. "Gosset graph 3_21". MathWorld.