6-orthoplex
| 6-orthoplex Hexacross | |
|---|---|
 Orthogonal projection inside Petrie polygon | |
| Type | Regular 6-polytope |
| Family | orthoplex |
| Schläfli symbols | {3,3,3,3,4} {3,3,3,31,1} |
| Coxeter-Dynkin diagrams | |
| 5-faces | 64 {34} |
| 4-faces | 192 {33} |
| Cells | 240 {3,3} |
| Faces | 160 {3} |
| Edges | 60 |
| Vertices | 12 |
| Vertex figure | 5-orthoplex |
| Petrie polygon | dodecagon |
| Coxeter groups | B6, [4,34] D6, [33,1,1] |
| Dual | 6-cube |
| Properties | convex, Hanner polytope |
In geometry, a 6-orthoplex, or 6-cross polytope, is a regular 6-polytope with 12 vertices, 60 edges, 160 triangle faces, 240 tetrahedron cells, 192 5-cell 4-faces, and 64 5-faces.
It has two constructed forms, the first being regular with Schläfli symbol {34,4}, and the second with alternately labeled (checkerboarded) facets, with Schläfli symbol {3,3,3,31,1} or Coxeter symbol 311.
It is a part of an infinite family of polytopes, called cross-polytopes or orthoplexes. The dual polytope is the 6-hypercube, or hexeract.
Alternate names
[edit]- Hexacross, derived from combining the family name cross polytope with hex for six (dimensions) in Greek.
- Hexacontitetrapeton as a 64-facetted 6-polytope.
As a configuration
[edit]This configuration matrix represents the 6-orthoplex. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-orthoplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[1][2]
Construction
[edit]There are three Coxeter groups associated with the 6-orthoplex, one regular, dual of the hexeract with the C6 or [4,3,3,3,3] Coxeter group, and a half symmetry with two copies of 5-simplex facets, alternating, with the D6 or [33,1,1] Coxeter group. A lowest symmetry construction is based on a dual of a 6-orthotope, called a 6-fusil.
| Name | Coxeter | Schläfli | Symmetry | Order |
|---|---|---|---|---|
| Regular 6-orthoplex | {3,3,3,3,4} | [4,3,3,3,3] | 46080 | |
| Quasiregular 6-orthoplex | {3,3,3,31,1} | [3,3,3,31,1] | 23040 | |
| 6-fusil | {3,3,3,4}+{} | [4,3,3,3,3] | 7680 | |
| {3,3,4}+{4} | [4,3,3,2,4] | 3072 | ||
| 2{3,4} | [4,3,2,4,3] | 2304 | ||
| {3,3,4}+2{} | [4,3,3,2,2] | 1536 | ||
| {3,4}+{4}+{} | [4,3,2,4,2] | 768 | ||
| 3{4} | [4,2,4,2,4] | 512 | ||
| {3,4}+3{} | [4,3,2,2,2] | 384 | ||
| 2{4}+2{} | [4,2,4,2,2] | 256 | ||
| {4}+4{} | [4,2,2,2,2] | 128 | ||
| 6{} | [2,2,2,2,2] | 64 |
Cartesian coordinates
[edit]Cartesian coordinates for the vertices of a 6-orthoplex, centered at the origin are
- (±1,0,0,0,0,0), (0,±1,0,0,0,0), (0,0,±1,0,0,0), (0,0,0,±1,0,0), (0,0,0,0,±1,0), (0,0,0,0,0,±1)
Every vertex pair is connected by an edge, except opposites.
Images
[edit]| Coxeter plane | B6 | B5 | B4 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [12] | [10] | [8] |
| Coxeter plane | B3 | B2 | |
| Graph | 
|

| |
| Dihedral symmetry | [6] | [4] | |
| Coxeter plane | A5 | A3 | |
| Graph | 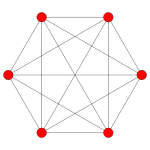
|

| |
| Dihedral symmetry | [6] | [4] |
Related polytopes
[edit]The 6-orthoplex can be projected down to 3-dimensions into the vertices of a regular icosahedron.[3]
| 2D | 3D | ||
|---|---|---|---|
 Icosahedron {3,5} = H3 Coxeter plane |
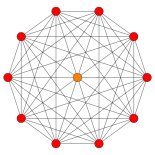 6-orthoplex {3,3,3,31,1} = D6 Coxeter plane |
 Icosahedron |
 6-orthoplex |
| This construction can be geometrically seen as the 12 vertices of the 6-orthoplex projected to 3 dimensions as the vertices of a regular icosahedron. This represents a geometric folding of the D6 to H3 Coxeter groups: | |||
It is in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 3k1 series. (A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral hosohedron.)
| Space | Finite | Euclidean | Hyperbolic | |||
|---|---|---|---|---|---|---|
| n | 4 | 5 | 6 | 7 | 8 | 9 |
| Coxeter group |
A3A1 | A5 | D6 | E7 | =E7+ | =E7++ |
| Coxeter diagram |
||||||
| Symmetry | [3−1,3,1] | [30,3,1] | [[31,3,1]] = [4,3,3,3,3] |
[32,3,1] | [33,3,1] | [34,3,1] |
| Order | 48 | 720 | 46,080 | 2,903,040 | ∞ | |
| Graph | 
|

|

|
- | - | |
| Name | 31,-1 | 310 | 311 | 321 | 331 | 341 |
This polytope is one of 63 uniform 6-polytopes generated from the B6 Coxeter plane, including the regular 6-cube or 6-orthoplex.
References
[edit]- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. 1966
- Klitzing, Richard. "6D uniform polytopes (polypeta) x3o3o3o3o4o - gee".
- Specific
- ^ Coxeter, Regular Polytopes, sec 1.8 Configurations
- ^ Coxeter, Complex Regular Polytopes, p.117
- ^ Quasicrystals and Geometry, Marjorie Senechal, 1996, Cambridge University Press, p64. 2.7.1 The I6 crystal
External links
[edit]- Olshevsky, George. "Cross polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary


































































