Pound–Rebka experiment

The Pound–Rebka experiment monitored frequency shifts in gamma rays as they rose and fell in the gravitational field of the Earth. The experiment tested Albert Einstein's 1907 and 1911 predictions, based on the equivalence principle, that photons would gain energy when descending a gravitational potential, and would lose energy when rising through a gravitational potential.[p 1][p 2] It was proposed by Robert Pound and his graduate student Glen A. Rebka Jr. in 1959,[p 3] and was the last of the classical tests of general relativity to be verified.[p 4] The measurement of gravitational redshift and blueshift by this experiment validated the prediction of the equivalence principle that clocks should be measured as running at different rates in different places of a gravitational field. It is considered to be the experiment that ushered in an era of precision tests of general relativity.
Background[edit]
Equivalence principle argument predicting gravitational red- and blueshift[edit]
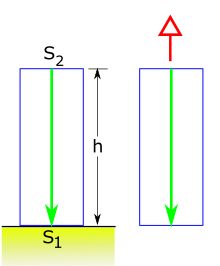
In the decade preceding Einstein's publication of the definitive version of his theory of general relativity, he anticipated several of the results of his final theory with heuristic arguments. One of these concerned the light in a gravitational field. To show that the equivalence principle implies that light is Doppler-shifted in a gravitational field, Einstein considered a light source separated along the z-axis by a distance above a receiver in a homogeneous gravitational field having a force per unit mass of 1 A continuous beam of electromagnetic energy with frequency is emitted by towards According to the equivalence principle, this system is equivalent to a gravitation-free system which moves with uniform acceleration in the direction of the positive z-axis, with separated by a constant distance from [p 2]
In the accelerated system, light emitted from takes (to a first approximation) to arrive at But in this time, the velocity of will have increased by from its velocity when the light was emitted. The frequency of light arriving at will therefore not be the frequency but the greater frequency given by
According to the equivalence principle, the same relation holds for the non-accelerated system in a gravitational field, where we replace by the gravitational potential difference between and so that[p 2]
Advent of general relativity[edit]
In 1916, Einstein used the framework of his newly completed general theory of relativity to update his earlier heuristic arguments predicting gravitational redshift to a more rigorous form.[p 5] Gravitational redshift and two other predictions from his 1916 paper, the anomalous perihelion precession of Mercury's orbit and the gravitational deflection of light by the Sun, have become known as the "classical tests" of general relativity. The anomalous perihelion precession of Mercury had long been recognized as a problem in celestial mechanics since the 1859 calculations of Urbain Le Verrier. The observation of the deflection of light by the Sun in the 1919 Eddington expedition catapulted Einstein to worldwide fame. Gravitational redshift would prove to be by far the most difficult of the three classical tests to demonstrate.
There had been little rush by experimenters to test Einstein's earlier predictions of gravitational time dilation, since the predicted effect was almost immeasurably small. Einstein's predicted displacement for spectral lines of the Sun amounted to only two parts in a million, and would be easily masked by line broadening due to temperature and pressure, and by line asymmetry due to the fact the lines represent the superposition of absorption from many turbulent layers of the solar atmosphere.[1] Several attempts to measure the effect were negative or inconclusive. The first generally accepted claim to have measured gravitational redshift was W.S. Adams's 1925 measurement of shifts in the spectral lines of the white dwarf star Sirius B.[2] However, even Adams's measurements have since been brought into question for various reasons.[3]
Mössbauer effect[edit]
In atomic spectroscopy, visible and ultraviolet photons resulting from electronic transitions of outer shell electrons, when emitted by gaseous atoms in an excited state, are readily absorbed by unexcited atoms of the same species. However, a corresponding absorbance of photons emitted by the nuclei of γ-emitters had never been observed because recoil of the nuclei resulted in so much loss of energy by the emitted photons that they no longer matched the absorbance spectra of the target nuclei. In 1958, Rudolf Mössbauer, who was analyzing the 129 keV transition of Iridium-191, discovered that by lowering the temperature of the emitter to 90K, he could achieve resonant absorbance. Indeed, the energy resolutions that he achieved were of unheard-of sharpness. He had discovered the phenomenon of recoilless γ-emission.[1][note 1]
In 1959, several research groups, most notably Robert Pound and Glen Rebka in Harvard and a team led by John Paul Schiffer in Harwell (England), announced plans to exploit this recently discovered effect to perform terrestrial tests of gravitational redshift.
In February 1960, Schiffer and his team were the first to announce success in measuring the gravitational redshift, but with a rather high error of ±47%.[p 6] It was to be Pound and Rebka's somewhat later contribution in April 1960, which used a stronger radiation source, longer path length, and several refinements to reduce systematic error, which was to be accepted as having provided a definitive measurement of the redshift.[p 4]
Pound and Rebka's experiment[edit]
Sources of error[edit]
After evaluating various γ-emitters for their study, Pound and Rebka chose to use 57Fe because it does not require cryogenic cooling to exhibit recoil-free emission, has a relatively low internal conversion coefficient[note 2] so that it is relatively free of competing X-ray emissions that would have been difficult to distinguish from the 14.4 keV transition,[note 3] and its parent 57Co has a usable half-life of 272 days.[5]
Pound and Rebka found that a large source of systematic error resulted from temperature variations, which they attributed primarily to a second order relativistic Doppler effect due to lattice vibrations. A mere 1°C difference in temperature between emitter and absorber caused a shift about equal to the predicted effect of gravitational time dilation.[p 7][6]
They also found frequency offsets between the lines of different combinations of source and absorber stemming from the sensitivity of the nuclear transition to an atom's physical and chemical environment.[note 4] They therefore needed to adopt methodology which would allow them to distinguish these offsets from their measurement of gravitational redshift. Extreme care was also needed in sample preparation, otherwise inhomogeneities would limit the sharpness of the lines.[p 4]
Experimental setup[edit]

The experiment was carried out in a tower at Harvard University's Jefferson laboratory that was, for the most part, vibrationally isolated from the rest of the building. An iron disk containing radioactive 57Co diffused into its surface was placed in the center of a ferroelectric or a moving coil magnetic transducer (speaker coil) which was placed near the roof of the building. A 38 cm diameter absorber consisting of thin square foils of iron enriched to a level of 32% 57Fe (as opposed to a 2% natural abundance), which were pasted side by side in a flat pattern on a Mylar sheet, was placed in the basement. The distance between the source and absorber was 22.5 meters (74 ft). The gamma rays traveled through a Mylar bag filled with helium to minimize scattering of the gamma rays. A scintillation counter was placed below the absorber to detect the gamma rays that passed through.[5]
The vibrating speaker coil imposed a continuously varying Doppler shift on the gamma ray source. Superimposed on the sinusoidal motions of the transducer was the slow (typically about 0.01 mm/s) constant motion of a slave hydraulic cylinder driven by a small diameter master cylinder controlled by a synchronous motor. The hydraulic cylinder motion was reversed multiple times during each data run after a constant integral number of transducer vibrations. Every several days, the position of the source and absorber would be reversed so that half the data runs would be of blueshift, and half would be of redshift.[5]
Three thermocouples mounted on the source in a spiral pattern and three on the absorber were connected to Wheatstone bridges to measure the temperature differences between the source and absorber. The recorded temperature differences were used to correct the data before analysis.[5]
Among the other steps used to compensate for possible systematic errors, Pound and Rebka varied the speaker frequency between 10 Hz and 50 Hz and tested different transducers (ferroelectric transducers versus moving coil magnetic speaker coils).[7]
A Mössbauer monitor near the source (not illustrated) checked for possible distortions of the source signal resulting from the cylinder/transducer assembly being regularly inverted from facing downwards to facing upwards.[5]
Modulation technique to detect small shifts[edit]

Although the 14.4 keV recoilless emission line of 57Fe had a half-width of 1.13×10−12, the anticipated gravitational frequency shift was only 2.5×10−15. Measurement of this minute amount of frequency shift, 500 times smaller than the half-width, required a sophisticated protocol for data acquisition and data analysis. The best way to measure a small shift is often by "slope detection", measuring the resonance not at its peak, but rather comparing the absorption curve near its points of maximum slope (inflection points) on either side of the peak.[5]
The speaker coil typically operated at about 74 Hz with a maximum velocity amplitude corresponding to the maximum change of absorption with velocity of the resonance curve for a given combination of source and absorber (typically around 0.10 mm/s).[note 5] Counts that were received in the quarter cycles of the oscillation period centered around the velocity maxima were accumulated in two separate registers. Likewise, counts received with the hydraulic cylinder in reverse motion were accumulated in another two separate registers, for a total of four registers of accumulated counts.[5]

The combined motions of the vibrating transducer and hydraulic cylinder allowed the incoming photons to be collected in four channels representing source motions of +0.11 mm/s, +0.09 mm/s, −0.11 mm/s, and −0.09 mm/s. They collectively operated at a 50% duty cycle, so that out of, say, 80 million incoming photons, 10 million would fit into the time slots of each of the four recording channels. From these counts, the velocity corresponding to the absorbance maximum could be calculated.[5]
The accuracy of determination of the line center depended on (1) the sharpness of the line, (2) the depth of the absorbance maximum, and (3) the total number of counts. They typically achieved a fractional absorbance maximum depth of about 0.3[5] and recorded about 1×1010 γ-rays, of which most will have been recoilless.[8][note 6]
Results[edit]
Each data run yielded eleven numbers, i.e. four absorber register counts, four monitor register counts, and three average temperature differences. The register counts were generally recorded after twelve full back-and-forth cycles of the hydraulic piston, where each reversal of piston motion occurred after 22,000 periods of source vibration.[5]
The source and absorber units were interchanged every several days to allow comparison between the results with the γ-rays rising versus the γ-rays falling. Combining data from runs having gravitational frequency shift of equal but opposite sign enabled the fixed frequency shift between a given source/target combination to be eliminated by subtraction.[5]
In their 1960 paper, Pound and Rebka presented data from the first four days of counting. Six runs with the source at the bottom, after temperature correction gave a weighted average fractional frequency shift between source and absorber of −(19.7±0.8)×10−15. Eight runs with the source at the top, after temperature correction gave a weighted average fractional frequency shift of −(15.5±0.8)×10−15.[p 4]
The frequency shifts, up and down, were both negative because the magnitude of the inherent frequency difference of the source/absorber combination considerably exceeded the magnitude of the expected gravitational redshifts/blueshifts. Taking half the sum of the weighted averages yielded the inherent frequency difference of the source/absorber combination, −(17.6±0.6)×10−15. Taking half the difference of the weighted averages yielded the net fractional frequency shift due to gravitational time dilation, −(2.1±0.5)×10−15.[p 4]
Over the full ten days of data collection, they calculated a net fractional frequency shift due to gravitational time dilation of −(2.56±0.25)×10−15, which corresponds to the predicted value with an error margin of 10%.[p 4]
In the next several years, the Pound lab published successive refinements of the gravitational redshift measurement, finally reaching the 1% level in 1964.[p 9][1]
Current status of gravitational redshift[edit]
In the years subsequent to the series of measurements performed by the Pound lab, various tests using other technologies established the validity of gravitational redshift/time dilation with increasing precision. A notable example was the 1976 Gravity Probe A experiment, which used a space-borne hydrogen maser to increase the accuracy of the measurement to about 0.01%.[p 10]
From an engineering standpoint, after the launch of the Global Positioning System (which depends on general relativity for its proper functioning[9]) and its integration into everyday life, gravitational redshift/time dilation is no longer considered a theoretical phenomenon requiring testing, but rather is considered a practical engineering concern in various fields requiring precision measurement, along with special relativity.[10]
From a theoretical standpoint, however, the status of gravitational redshift/time dilation is quite different. It is widely recognized that general relativity, despite accounting for all data gathered to date, cannot represent a final theory of nature.[11]
The equivalence principle (EP) lies at the heart of the general theory of relativity. Most proposed alternatives to general relativity predict violation of the EP at some level. The EP includes three hypotheses:[11]
- Universality of free fall (UFF). This asserts that the acceleration of bodies freely falling bodies in a gravitational field is independent of their compositions.
- Local Lorentz invariance (LLI). This asserts that the outcome of a local experiment is independent of the velocity and orientation of the apparatus.
- Local position invariance (LPI). This asserts that clock rates are independent of their spacetime positions. Measurements of differences in the elapsed time displayed by two clocks will depend on their relative positioning in a gravitational field. But the clocks themselves are unaffected by gravitational potential.
Gravitational redshift measurements provide a direct measure of LPI. Of the three hypotheses underlying the equivalence principle, LPI has been by far the least accurately determined. There has been considerable incentive, therefore, to improve on gravitational redshift measurements both in the laboratory and using astronomical observations.[11] For example, the much anticipated, and much delayed European Space Agency's Atomic Clock Ensemble in Space (ACES) mission is expected to improve on previous measurements by a factor of 35.[p 11]
Notes[edit]
- ^ Mössbauer's discovery paper was initially greeted with widespread disbelief among the physics community, most of whom did not consider such sharp resonances to be possible. Anecdotally, it has been related that Frauenfelder[4] only conducted his confirmatory experiment to win a five-cent bet.[1]
- ^ An excited nucleus, instead of emitting a γ-ray, may interact with an inner shell electron causing the electron's ejection. This leaves a hole in the electron shell which is filled in by other electrons with the release of characteristic X-rays.
- ^ In 1959, γ-ray spectrometers capable of clearly distinguishing the desired 14.4 keV emissions from X-rays resulting from internal conversion were not yet available.[5]
- ^ Indeed, the exquisite sensitivity of the nuclear transition to small changes in the chemical environment underlies the Mössbauer effect's usefulness in Mössbauer spectroscopy.
- ^ If we presume that the profile of the absorption curve has a Lorentzian distribution, then the inflection points would lie times the half-widths of the curve on either side of the absorption peak. Their source/absorber combinations typically exhibited half-widths of 0.17 mm/s.[6]
- ^ This is a straightforward estimate assuming a 0.4 Ci source, 10 days of data collection, an internal conversion coefficient of 9, and a 50% duty cycle. The percentage of recoilless emission/absorption is given by the Lamb–Mössbauer factor, which for polycrystalline iron at room temperature has been measured as about 80%.[p 8]
Primary sources[edit]
- ^ Einstein, Albert (1907). "On the relativity principle and the conclusions drawn from it". In Stachel, John; Cassidy, David C; Renn, Jürgen; et al. (eds.). The Collected Papers of Albert Einstein, Volume 2: The Swiss Years: Writings, 1900-1909. Princeton: Princeton University Press. p. 252. ISBN 9780691085265. Retrieved 2 August 2015.
- ^ a b c Einstein, Albert (1911). "On the Influence of Gravitation on the Propagation of Light". In Klein, Martin; Kox, A. J.; Renn, Jurgen; Schulman, Robert (eds.). The Collected Papers of Albert Einstein. Volume 3: Writings 1909-1911 (English translation supplement). Translated by Beck, Anna. Princeton University Press. p. 485. ISBN 9780691102504.
- ^ Pound, R. V.; Rebka Jr. G. A. (November 1, 1959). "Gravitational Red-Shift in Nuclear Resonance". Physical Review Letters. 3 (9): 439–441. Bibcode:1959PhRvL...3..439P. doi:10.1103/PhysRevLett.3.439.
- ^ a b c d e f Pound, R. V.; Rebka Jr. G. A. (April 1, 1960). "Apparent weight of photons". Physical Review Letters. 4 (7): 337–341. Bibcode:1960PhRvL...4..337P. doi:10.1103/PhysRevLett.4.337.
- ^ Einstein, Albert (1916). "The Foundation of the General Theory of Relativity" (English HTML, contains link to German PDF). Annalen der Physik. 49 (7): 769–822. Bibcode:1916AnP...354..769E. doi:10.1002/andp.19163540702.
- ^ Cranshaw, T. E.; Schiffer, J. P.; Whitehead, A. B. (1960). "Measurement of the Gravitational Red Shift Using the Mössbauer Effect in Fe57". Physical Review Letters. 4 (4): 163. Bibcode:1960PhRvL...4..163C. doi:10.1103/PhysRevLett.4.163.
- ^ Pound, R. V.; Rebka, Jr., G. A. (1960). "Variation with Temperature of the Energy of Recoil-Free Gamma Rays from Solids". Physical Review Letters. 4 (6): 274. Bibcode:1960PhRvL...4..274P. doi:10.1103/PhysRevLett.4.274.
- ^ Sturhahn, Wolfgang; Chumakov, A. (1999). "Lamb–Mössbauer factor and second-order Doppler shift from inelastic nuclear resonant absorption". Hyperfine Interactions. 123 (1–4): 809–824. doi:10.1023/A:1017060931911. S2CID 92448841.
- ^ Pound, R. V.; Snider J. L. (November 2, 1964). "Effect of Gravity on Nuclear Resonance". Physical Review Letters. 13 (18): 539–540. Bibcode:1964PhRvL..13..539P. doi:10.1103/PhysRevLett.13.539.
- ^ Vessot, R. F. C.; M. W. Levine; E. M. Mattison; E. L. Blomberg; T. E. Hoffman; G. U. Nystrom; B. F. Farrel; R. Decher; P. B. Eby; C. R. Baugher; J. W. Watts; D. L. Teuber; F. D. Wills (December 29, 1980). "Test of Relativistic Gravitation with a Space-Borne Hydrogen Maser". Physical Review Letters. 45 (26): 2081–2084. Bibcode:1980PhRvL..45.2081V. doi:10.1103/PhysRevLett.45.2081.
- ^ Savalle, Etienne; Guerlin, Christine; Delva, Pacôme; Meynadier, Frédéric; le Poncin-Lafitte, Christophe; Wolf, Peter (2019). "Gravitational redshift test with the future ACES mission". Classical and Quantum Gravity. 36 (24): 245004. arXiv:1907.12320. Bibcode:2019CQGra..36x5004S. doi:10.1088/1361-6382/ab4f25. S2CID 198967934.
References[edit]
- ^ a b c d Hentschel, Klaus (1996). "Measurements of Gravitational Redshift between 1959 and 1971". Annals of Science. 53 (3): 269–295. doi:10.1080/00033799600200211.
- ^ Hetherington, N. S., "Sirius B and the gravitational redshift - an historical review", Quarterly Journal Royal Astronomical Society, vol. 21, Sept. 1980, p. 246-252. Accessed 6 April 2017.
- ^ Holberg, J. B., "Sirius B and the Measurement of the Gravitational Redshift", Journal for the History of Astronomy, Vol. 41, 1, 2010, p. 41-64. Accessed 6 April 2017.
- ^ Frauenfelder, Hans (1962). The Mossbauer effect. New York: Benjamin.
- ^ a b c d e f g h i j k l Pound, R. V. (1981). "The Gravitational Red-Shift". In Gonser, Ulrich (ed.). Molecular Spectroscopy II: The Exotic Side of the Method. Berlin: Springer-Verlag. p. 31. ISBN 978-3-662-08869-2.
- ^ a b Kock, Winston E. (1960). "The Mössbauer Radiation: Low-energy gamma rays provide the most precisely defined electromagnetic frequency yet discovered". Science. 131 (3413): 1588–1590. doi:10.1126/science.131.3413.1588. PMID 17745302.
- ^ Mester, John (2006). "Experimental Tests of General Relativity" (PDF). LUTH - Observatoire de Paris: 9–11. Retrieved 2007-04-13.
- ^ Fultz, Brent (2011). "Mössbauer Spectroscopy". In Kaufmann, Elton (ed.). Characteriation of Materials (PDF). New York: John Wiley. Retrieved 26 February 2023.
- ^ Ashby, Neil (2003). "Relativity in the Global Positioning System". Living Reviews in Relativity. 6 (1): 1. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. PMC 5253894. PMID 28163638.
- ^ Francis, S.; Ramsey, B.; Stein, S.; Leitner, J.; Moreau, M.; Burns, R.; Nelson, R. A.; Bartholomew, T. R.; Gifford, A. (2002). "Timekeeping and time dissemination in a distributed space-based clock ensemble" (PDF). 34th Annual Precise Time and Time Interval Systems and Applications Meeting: 201–214. Archived from the original (PDF) on 2004-02-01. Retrieved 24 February 2023.
- ^ a b c Turyshev, Slava G. (2008). "Experimental tests of general relativity". Annual Review of Nuclear and Particle Science. 58 (1): 207–248. arXiv:0806.1731. Bibcode:2008ARNPS..58..207T. doi:10.1146/annurev.nucl.58.020807.111839. S2CID 119199160. Retrieved 5 March 2023.
External links[edit]
- Horowitz, Paul (Fall 2021). "TESTING EINSTEIN'S PREDICTION: The Pound–Rebka Experiment" (PDF). Physics: Harvard University Department of Physics Newsletter: 12. Retrieved 28 February 2023.
- Lindley, David (2005). "The Weight of Light". Physical Review Focus. Vol. 16. p. 1. Retrieved 6 March 2023.
















