Tests of general relativity
| General relativity |
|---|
 |
Tests of general relativity serve to establish observational evidence for the theory of general relativity. The first three tests, proposed by Albert Einstein in 1915, concerned the "anomalous" precession of the perihelion of Mercury, the bending of light in gravitational fields, and the gravitational redshift. The precession of Mercury was already known; experiments showing light bending in accordance with the predictions of general relativity were performed in 1919, with increasingly precise measurements made in subsequent tests; and scientists claimed to have measured the gravitational redshift in 1925, although measurements sensitive enough to actually confirm the theory were not made until 1954. A more accurate program starting in 1959 tested general relativity in the weak gravitational field limit, severely limiting possible deviations from the theory.
In the 1970s, scientists began to make additional tests, starting with Irwin Shapiro's measurement of the relativistic time delay in radar signal travel time near the Sun. Beginning in 1974, Hulse, Taylor and others studied the behaviour of binary pulsars experiencing much stronger gravitational fields than those found in the Solar System. Both in the weak field limit (as in the Solar System) and with the stronger fields present in systems of binary pulsars the predictions of general relativity have been extremely well tested.
In February 2016, the Advanced LIGO team announced that they had directly detected gravitational waves from a black hole merger.[1] This discovery, along with additional detections announced in June 2016 and June 2017,[2] tested general relativity in the very strong field limit, observing to date no deviations from theory.
Classical tests[edit]
Albert Einstein proposed[3][4] three tests of general relativity, subsequently called the "classical tests" of general relativity, in 1916:
- the perihelion precession of Mercury's orbit
- the deflection of light by the Sun
- the gravitational redshift of light
In the letter to The Times (of London) on November 28, 1919, he described the theory of relativity and thanked his English colleagues for their understanding and testing of his work. He also mentioned three classical tests with comments:[5]
- "The chief attraction of the theory lies in its logical completeness. If a single one of the conclusions drawn from it proves wrong, it must be given up; to modify it without destroying the whole structure seems to be impossible."
Perihelion precession of Mercury[edit]

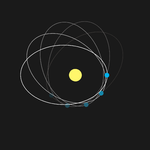
Under Newtonian physics, an object in an (isolated) two-body system, consisting of the object orbiting a spherical mass, would trace out an ellipse with the center of mass of the system at a focus of the ellipse. The point of closest approach, called the periapsis (or when the central body is the Sun, perihelion), is fixed. Hence the major axis of the ellipse remains fixed in space. Both objects orbit around the center of mass of this system, so they each have their own ellipse. However, a number of effects in the Solar System cause the perihelia of planets to precess (rotate) around the Sun in the plane of their orbits, or equivalently, cause the major axis to rotate about the center of mass, hence changing its orientation in space.[6] The principal cause is the presence of other planets which perturb one another's orbit. Another (much less significant) effect is solar oblateness.
Mercury deviates from the precession predicted from these Newtonian effects. This anomalous rate of precession of the perihelion of Mercury's orbit was first recognized in 1859 as a problem in celestial mechanics, by Urbain Le Verrier. His re-analysis of available timed observations of transits of Mercury over the Sun's disk from 1697 to 1848 showed that the actual rate of the precession disagreed from that predicted from Newton's theory by 38″ (arcseconds) per tropical century (later re-estimated at 43″ by Simon Newcomb in 1882).[7] A number of ad hoc and ultimately unsuccessful solutions were proposed, but they tended to introduce more problems. Le Verrier suggested that another hypothetical planet might exist to account for Mercury's behavior.[7] The previously successful search for Neptune based on its perturbations of the orbit of Uranus led astronomers to place some faith in this possible explanation, and the hypothetical planet was even named Vulcan. Finally, in 1908, W. W. Campbell, Director of the Lick Observatory, after the comprehensive photographic observations by Lick astronomer, Charles D. Perrine, at three solar eclipse expeditions, stated, "In my opinion, Dr. Perrine's work at the three eclipses of 1901, 1905, and 1908 brings the observational side of the famous intramercurial-planet problem definitely to a close."[8][9] Subsequently, no evidence of Vulcan was found and Einstein's 1915 general theory accounted for Mercury's anomalous precession. Einstein wrote to Michael Besso, "Perihelion motions explained quantitatively ... you will be astonished".[10]
In general relativity, this remaining precession, or change of orientation of the orbital ellipse within its orbital plane, is explained by gravitation being mediated by the curvature of spacetime. Einstein showed that general relativity[3] agrees closely with the observed amount of perihelion shift. This was a powerful factor motivating the adoption of general relativity.
Although earlier measurements of planetary orbits were made using conventional telescopes, more accurate measurements are now made with radar. The total observed precession of Mercury is (574.10 ± 0.65)″ per century[11] relative to the inertial ICRF. This precession can be attributed to the following causes:
| Amount (arcsec/Julian century)[12] | Cause |
|---|---|
| 532.3035 | gravitational tugs of other solar bodies |
| 0.0286 | oblateness of the Sun (quadrupole moment) |
| 42.9799 | gravitoelectric effects (Schwarzschild-like), a general relativity effect |
| −0.0020 | Lense–Thirring precession |
| 575.31[12] | total predicted |
| 574.10 ± 0.65[11] | observed |
The correction by (42.980 ± 0.001)″/cy is the prediction of post-Newtonian theory with parameters .[13] Thus the effect can be fully explained by general relativity. More recent calculations based on more precise measurements have not materially changed the situation.
In general relativity the perihelion shift σ, expressed in radians per revolution, is approximately given by:[14]
where L is the semi-major axis, T is the orbital period, c is the speed of light, and e is the orbital eccentricity (see: Two-body problem in general relativity).
The other planets experience perihelion shifts as well, but, since they are farther from the Sun and have longer periods, their shifts are lower, and could not be observed accurately until long after Mercury's. For example, the perihelion shift of Earth's orbit due to general relativity is theoretically 3.83868″ per century and experimentally (3.8387 ± 0.0004)″/cy, Venus's is 8.62473″/cy and (8.6247 ± 0.0005)″/cy and Mars' is (1.351 ± 0.001)″/cy. Both values have now been measured, with results in good agreement with theory.[15] The periapsis shift has also now been measured for binary pulsar systems, with PSR 1913+16 amounting to 4.2° per year.[16] These observations are consistent with general relativity.[17] It is also possible to measure periapsis shift in binary star systems which do not contain ultra-dense stars, but it is more difficult to model the classical effects precisely – for example, the alignment of the stars' spin to their orbital plane needs to be known and is hard to measure directly. A few systems, such as DI Herculis,[18] have been measured as test cases for general relativity.
Deflection of light by the Sun[edit]

Henry Cavendish in 1784 (in an unpublished manuscript) and Johann Georg von Soldner in 1801 (published in 1804) had pointed out that Newtonian gravity predicts that starlight will bend around a massive object.[19][20] The same value as Soldner's was calculated by Einstein in 1911 based on the equivalence principle alone. However, Einstein noted in 1915 in the process of completing general relativity, that his 1911 result (and thus Soldner's 1801 result) is only half of the correct value. Einstein became the first to calculate the correct value for light bending: 1.75 arcseconds for light that grazes the Sun.[21][22]
The first observation of light deflection was performed by noting the change in position of stars as they passed near the Sun on the celestial sphere. The observations were performed by Arthur Eddington and his collaborators (see Eddington experiment) during the total solar eclipse of May 29, 1919,[23] when the stars near the Sun (at that time in the constellation Taurus) could be observed.[23] Observations were made simultaneously in the cities of Sobral, Ceará, Brazil and in São Tomé and Príncipe on the west coast of Africa.[24] The result was considered spectacular news and made the front page of most major newspapers. It made Einstein and his theory of general relativity world-famous. When asked by his assistant what his reaction would have been if general relativity had not been confirmed by Eddington and Dyson in 1919, Einstein famously made the quip: "Then I would feel sorry for the dear Lord. The theory is correct anyway."[25]
The early accuracy, however, was poor and there was doubt that the small number of measured star locations and instrument questions could produce a reliable result. The results were argued by some[26] to have been plagued by systematic error and possibly confirmation bias, although modern reanalysis of the dataset[27] suggests that Eddington's analysis was accurate.[28][29] The measurement was repeated by a team from the Lick Observatory led by the Director W. W. Campbell in the 1922 eclipse as observed in remote Australian station of Wallal,[30] with results based on hundreds of star positions that agreed with the 1919 results[29] and has been repeated several times since, most notably in 1953 by Yerkes Observatory astronomers[31] and in 1973 by a team from the University of Texas.[32] Considerable uncertainty remained in these measurements for almost fifty years, until observations started being made at radio frequencies.[33][34] The deflection of starlight by the nearby white dwarf star Stein 2051 B has also been measured.[35]
Gravitational redshift of light[edit]

Einstein predicted the gravitational redshift of light from the equivalence principle in 1907, and it was predicted that this effect might be measured in the spectral lines of a white dwarf star, which has a very high gravitational field. Initial attempts to measure the gravitational redshift of the spectrum of Sirius-B, were done by Walter Sydney Adams in 1925, but the result was criticized as being unusable due to the contamination from light from the (much brighter) primary star, Sirius.[36][37] The first accurate measurement of the gravitational redshift of a white dwarf was done by Popper in 1954, measuring a 21 km/s gravitational redshift of 40 Eridani B.[37]
The redshift of Sirius B was finally measured by Greenstein et al. in 1971, obtaining the value for the gravitational redshift of 89±16 km/s, with more accurate measurements by the Hubble Space Telescope showing 80.4±4.8 km/s.[38]
Tests of special relativity[edit]
The general theory of relativity incorporates Einstein's special theory of relativity, and hence tests of special relativity are also testing aspects of general relativity. As a consequence of the equivalence principle, Lorentz invariance holds locally in non-rotating, freely falling reference frames. Experiments related to Lorentz invariance special relativity (that is, when gravitational effects can be neglected) are described in tests of special relativity.
Modern tests[edit]
The modern era of testing general relativity was ushered in largely at the impetus of Dicke and Schiff who laid out a framework for testing general relativity.[39][40][41] They emphasized the importance not only of the classical tests, but of null experiments, testing for effects which in principle could occur in a theory of gravitation, but do not occur in general relativity. Other important theoretical developments included the inception of alternative theories to general relativity, in particular, scalar–tensor theories such as the Brans–Dicke theory;[42] the parameterized post-Newtonian formalism in which deviations from general relativity can be quantified; and the framework of the equivalence principle.
Experimentally, new developments in space exploration, electronics and condensed matter physics have made additional precise experiments possible, such as the Pound–Rebka experiment, laser interferometry and lunar rangefinding.
Post-Newtonian tests of gravity[edit]
Early tests of general relativity were hampered by the lack of viable competitors to the theory: it was not clear what sorts of tests would distinguish it from its competitors. General relativity was the only known relativistic theory of gravity compatible with special relativity and observations. Moreover, it is an extremely simple and elegant theory.[according to whom?] This changed with the introduction of Brans–Dicke theory in 1960. This theory is arguably simpler, as it contains no dimensionful constants, and is compatible with a version of Mach's principle and Dirac's large numbers hypothesis, two philosophical ideas which have been influential in the history of relativity. Ultimately, this led to the development of the parametrized post-Newtonian formalism by Nordtvedt and Will, which parametrizes, in terms of ten adjustable parameters, all the possible departures from Newton's law of universal gravitation to first order in the velocity of moving objects (i.e. to first order in , where v is the velocity of an object and c is the speed of light). This approximation allows the possible deviations from general relativity, for slowly moving objects in weak gravitational fields, to be systematically analyzed. Much effort has been put into constraining the post-Newtonian parameters, and deviations from general relativity are at present severely limited.
The experiments testing gravitational lensing and light time delay limits the same post-Newtonian parameter, the so-called Eddington parameter γ, which is a straightforward parametrization of the amount of deflection of light by a gravitational source. It is equal to one for general relativity, and takes different values in other theories (such as Brans–Dicke theory). It is the best constrained of the ten post-Newtonian parameters, but there are other experiments designed to constrain the others. Precise observations of the perihelion shift of Mercury constrain other parameters, as do tests of the strong equivalence principle.
One of the goals of the BepiColombo mission to Mercury, is to test the general relativity theory by measuring the parameters gamma and beta of the parametrized post-Newtonian formalism with high accuracy.[43][44] The experiment is part of the Mercury Orbiter Radio science Experiment (MORE).[45][46] The spacecraft was launched in October 2018 and is expected to enter orbit around Mercury in December 2025.
Gravitational lensing[edit]
One of the most important tests is gravitational lensing. It has been observed in distant astrophysical sources, but these are poorly controlled and it is uncertain how they constrain general relativity. The most precise tests are analogous to Eddington's 1919 experiment: they measure the deflection of radiation from a distant source by the Sun. The sources that can be most precisely analyzed are distant radio sources. In particular, some quasars are very strong radio sources. The directional resolution of any telescope is in principle limited by diffraction; for radio telescopes this is also the practical limit. An important improvement in obtaining positional high accuracies (from milli-arcsecond to micro-arcsecond) was obtained by combining radio telescopes across Earth. The technique is called very long baseline interferometry (VLBI). With this technique radio observations couple the phase information of the radio signal observed in telescopes separated over large distances. Recently, these telescopes have measured the deflection of radio waves by the Sun to extremely high precision, confirming the amount of deflection predicted by general relativity aspect to the 0.03% level.[47] At this level of precision systematic effects have to be carefully taken into account to determine the precise location of the telescopes on Earth. Some important effects are Earth's nutation, rotation, atmospheric refraction, tectonic displacement and tidal waves. Another important effect is refraction of the radio waves by the solar corona. Fortunately, this effect has a characteristic spectrum, whereas gravitational distortion is independent of wavelength. Thus, careful analysis, using measurements at several frequencies, can subtract this source of error.
The entire sky is slightly distorted due to the gravitational deflection of light caused by the Sun (the anti-Sun direction excepted). This effect has been observed by the European Space Agency astrometric satellite Hipparcos. It measured the positions of about 105 stars. During the full mission about 3.5×106 relative positions have been determined, each to an accuracy of typically 3 milliarcseconds (the accuracy for an 8–9 magnitude star). Since the gravitation deflection perpendicular to the Earth–Sun direction is already 4.07 milliarcseconds, corrections are needed for practically all stars. Without systematic effects, the error in an individual observation of 3 milliarcseconds, could be reduced by the square root of the number of positions, leading to a precision of 0.0016 milliarcseconds. Systematic effects, however, limit the accuracy of the determination to 0.3% (Froeschlé, 1997).
Launched in 2013, the Gaia spacecraft will conduct a census of one billion stars in the Milky Way and measure their positions to an accuracy of 24 microarcseconds. Thus it will also provide stringent new tests of gravitational deflection of light caused by the Sun which was predicted by General relativity.[48]
Light travel time delay testing[edit]
Irwin I. Shapiro proposed another test, beyond the classical tests, which could be performed within the Solar System. It is sometimes called the fourth "classical" test of general relativity. He predicted a relativistic time delay (Shapiro delay) in the round-trip travel time for radar signals reflecting off other planets.[49] The mere curvature of the path of a photon passing near the Sun is too small to have an observable delaying effect (when the round-trip time is compared to the time taken if the photon had followed a straight path), but general relativity predicts a time delay that becomes progressively larger when the photon passes nearer to the Sun due to the time dilation in the gravitational potential of the Sun. Observing radar reflections from Mercury and Venus just before and after they are eclipsed by the Sun agrees with general relativity theory at the 5% level.[50]
More recently, the Cassini probe has undertaken a similar experiment which gave agreement with general relativity at the 0.002% level.[51] However, the following detailed studies[52][53] revealed that the measured value of the PPN parameter gamma is affected by gravitomagnetic effect caused by the orbital motion of Sun around the barycenter of the solar system. The gravitomagnetic effect in the Cassini radioscience experiment was implicitly postulated by B. Bertotti as having a pure general relativistic origin but its theoretical value has never been tested in the experiment which effectively makes the experimental uncertainty in the measured value of gamma actually larger (by a factor of 10) than 0.002% claimed by B. Bertotti and co-authors in Nature.
Very Long Baseline Interferometry has measured velocity-dependent (gravitomagnetic) corrections to the Shapiro time delay in the field of moving Jupiter[54][55] and Saturn.[56]
Equivalence principle[edit]
The equivalence principle, in its simplest form, asserts that the trajectories of falling bodies in a gravitational field should be independent of their mass and internal structure, provided they are small enough not to disturb the environment or be affected by tidal forces. This idea has been tested to extremely high precision by Eötvös torsion balance experiments, which look for a differential acceleration between two test masses. Constraints on this, and on the existence of a composition-dependent fifth force or gravitational Yukawa interaction are very strong, and are discussed under fifth force and weak equivalence principle.
A version of the equivalence principle, called the strong equivalence principle, asserts that self-gravitation falling bodies, such as stars, planets or black holes (which are all held together by their gravitational attraction) should follow the same trajectories in a gravitational field, provided the same conditions are satisfied. This is called the Nordtvedt effect and is most precisely tested by the Lunar Laser Ranging Experiment.[57][58] Since 1969, it has continuously measured the distance from several rangefinding stations on Earth to reflectors on the Moon to approximately centimeter accuracy.[59] These have provided a strong constraint on several of the other post-Newtonian parameters.
Another part of the strong equivalence principle is the requirement that Newton's gravitational constant be constant in time, and have the same value everywhere in the universe. There are many independent observations limiting the possible variation of Newton's gravitational constant,[60] but one of the best comes from lunar rangefinding which suggests that the gravitational constant does not change by more than one part in 1011 per year. The constancy of the other constants is discussed in the Einstein equivalence principle section of the equivalence principle article.
Gravitational redshift and time dilation[edit]
The first of the classical tests discussed above, the gravitational redshift, is a simple consequence of the Einstein equivalence principle and was predicted by Einstein in 1907. As such, it is not a test of general relativity in the same way as the post-Newtonian tests, because any theory of gravity obeying the equivalence principle should also incorporate the gravitational redshift. Nonetheless, confirming the existence of the effect was an important substantiation of relativistic gravity, since the absence of gravitational redshift would have strongly contradicted relativity. The first observation of the gravitational redshift was the measurement of the shift in the spectral lines from the white dwarf star Sirius B by Adams in 1925, discussed above, and follow-on measurements of other white dwarfs. Because of the difficulty of the astrophysical measurement, however, experimental verification using a known terrestrial source was preferable.
Experimental verification of gravitational redshift using terrestrial sources took several decades, because it is difficult to find clocks (to measure time dilation) or sources of electromagnetic radiation (to measure redshift) with a frequency that is known well enough that the effect can be accurately measured. It was confirmed experimentally for the first time in 1959 using measurements of the change in wavelength of gamma-ray photons generated with the Mössbauer effect, which generates radiation with a very narrow line width. The Pound–Rebka experiment measured the relative redshift of two sources situated at the top and bottom of Harvard University's Jefferson tower.[61][62] The result was in excellent agreement with general relativity. This was one of the first precision experiments testing general relativity. The experiment was later improved to better than the 1% level by Pound and Snider.[63]
The blueshift of a falling photon can be found by assuming it has an equivalent mass based on its frequency E = hf (where h is the Planck constant) along with E = mc2, a result of special relativity. Such simple derivations ignore the fact that in general relativity the experiment compares clock rates, rather than energies. In other words, the "higher energy" of the photon after it falls can be equivalently ascribed to the slower running of clocks deeper in the gravitational potential well. To fully validate general relativity, it is important to also show that the rate of arrival of the photons is greater than the rate at which they are emitted. A very accurate gravitational redshift experiment, which deals with this issue, was performed in 1976,[64] where a hydrogen maser clock on a rocket was launched to a height of 10,000 km, and its rate compared with an identical clock on the ground. It tested the gravitational redshift to 0.007%.
Although the Global Positioning System (GPS) is not designed as a test of fundamental physics, it must account for the gravitational redshift in its timing system, and physicists have analyzed timing data from the GPS to confirm other tests. When the first satellite was launched, some engineers resisted the prediction that a noticeable gravitational time dilation would occur, so the first satellite was launched without the clock adjustment that was later built into subsequent satellites. It showed the predicted shift of 38 microseconds per day. This rate of discrepancy is sufficient to substantially impair function of GPS within hours if not accounted for. An excellent account of the role played by general relativity in the design of GPS can be found in Ashby 2003.[65]
Other precision tests of general relativity,[66] not discussed here, are the Gravity Probe A satellite, launched in 1976, which showed gravity and velocity affect the ability to synchronize the rates of clocks orbiting a central mass and the Hafele–Keating experiment, which used atomic clocks in circumnavigating aircraft to test general relativity and special relativity together.[67][68]
Frame-dragging tests[edit]

Tests of the Lense–Thirring precession, consisting of small secular precessions of the orbit of a test particle in motion around a central rotating mass, for example, a planet or a star, have been performed with the LAGEOS satellites,[69] but many aspects of them remain controversial. The same effect may have been detected in the data of the Mars Global Surveyor (MGS) spacecraft, a former probe in orbit around Mars; also such a test raised a debate.[70] First attempts to detect the Sun's Lense–Thirring effect on the perihelia of the inner planets have been recently reported as well. Frame dragging would cause the orbital plane of stars orbiting near a supermassive black hole to precess about the black hole spin axis. This effect should be detectable within the next few years via astrometric monitoring of stars at the center of the Milky Way galaxy.[71] By comparing the rate of orbital precession of two stars on different orbits, it is possible in principle to test the no-hair theorems of general relativity.[72]
The Gravity Probe B satellite, launched in 2004 and operated until 2005, detected frame-dragging and the geodetic effect. The experiment used four quartz spheres the size of ping pong balls coated with a superconductor. Data analysis continued through 2011 due to high noise levels and difficulties in modelling the noise accurately so that a useful signal could be found. Principal investigators at Stanford University reported on May 4, 2011, that they had accurately measured the frame dragging effect relative to the distant star IM Pegasi, and the calculations proved to be in line with the prediction of Einstein's theory. The results, published in Physical Review Letters measured the geodetic effect with an error of about 0.2 percent. The results reported the frame dragging effect (caused by Earth's rotation) added up to 37 milliarcseconds with an error of about 19 percent.[73] Investigator Francis Everitt explained that a milliarcsecond "is the width of a human hair seen at the distance of 10 miles".[74]
In January 2012, LARES satellite was launched on a Vega rocket[75] to measure Lense–Thirring effect with an accuracy of about 1%, according to its proponents.[76] This evaluation of the actual accuracy obtainable is a subject of debate.[77][78][79]
Tests of the gravitational potential at small distances[edit]
It is possible to test whether the gravitational potential continues with the inverse square law at very small distances. Tests so far have focused on a divergence from GR in the form of a Yukawa potential , but no evidence for a potential of this kind has been found. The Yukawa potential with has been ruled out down to λ = 5.6×10−5 m.[80]
Mössbauer rotor experiment[edit]
It was conceived as a means to measure the time dilation effect on Earth after being motivated by Einstein's equivalence principle that implies a rotating observer will be subject to the same transformations as an observer in a gravitational field.[81] Mössbauer rotor experiments hence permit a precise terrestrial test of the relativistic Doppler effect. From a radioactive source fixed at the center of a spinning disc or rod, gamma rays travel to an absorber at the rim (in some variations of the experiment this scheme was reversed) and an unabsorbed number of them pass through depending on the rotational speed to arrive at a stationary counter (i.e., detector of gamma quanta resting in the lab frame). In lieu with the Clock hypothesis, Einstein's general relativity predicts that the moving absorber's clock at the rim should retard by a specific amount due to time dilation on account of centrifugal binding alone compared to a rest frame absorber. So the transmission of gamma photons through the absorber should increase during rotation, which can be subsequently measured by the stationary counter beyond the absorber. This prediction was actually observed using the Mössbauer effect, since the equivalence principle, as originally suggested by Einstein, implicitly allows the association of the time dilation due to rotation (calculated as a result of the change in the detector's count rate) with gravitational time dilation. Such experiments were pioneered by Hay et al. (1960),[82] Champeney et al. (1965),[83] and Kündig (1963),[84] and all of them had declared confirmation of the prediction of Einstein's theory of relativity.
Be that as it may, an early 21st Century re-examination of these endeavors called into question the validity of the past obtained results claiming to have verified time dilation as predicted by Einstein's relativity theory,[85][86] whereby novel experimentations were carried out that uncovered an extra energy shift between emitted and absorbed radiation next to the classical relativistic dilation of time.[87][88] This discovery was first explained as discrediting general relativity and successfully confirming at the laboratory scale the predictions of an alternative theory of gravity developed by T. Yarman and his colleagues.[89] Against this development, a contentious attempt was made to explain the disclosed extra energy shift as arising from a so-far unknown and allegedly missed clock synchronization effect,[90][91] which was unusually awarded a prize in 2018 by the Gravity Research Foundation for having secured a new proof of general relativity.[92] However, at the same time period, it was revealed that said author committed several mathematical errors in his calculations,[93] and the supposed contribution of the so-called clock synchronization to the measured time dilation is in fact practically null.[94][95][96][97][98][99] As a consequence, a general relativistic explanation for the outcomes of Mössbauer rotor experiments remains open.
Strong field tests[edit]
The very strong gravitational fields that are present close to black holes, especially those supermassive black holes which are thought to power active galactic nuclei and the more active quasars, belong to a field of intense active research. Observations of these quasars and active galactic nuclei are difficult, and interpretation of the observations is heavily dependent upon astrophysical models other than general relativity or competing fundamental theories of gravitation, but they are qualitatively consistent with the black hole concept as modeled in general relativity.
Binary pulsars[edit]
Pulsars are rapidly rotating neutron stars which emit regular radio pulses as they rotate. As such they act as clocks which allow very precise monitoring of their orbital motions. Observations of pulsars in orbit around other stars have all demonstrated substantial periapsis precessions that cannot be accounted for classically but can be accounted for by using general relativity. For example, the Hulse–Taylor binary pulsar PSR B1913+16 (a pair of neutron stars in which one is detected as a pulsar) has an observed precession of over 4° of arc per year (periastron shift per orbit only about 10−6). This precession has been used to compute the masses of the components.
Similarly to the way in which atoms and molecules emit electromagnetic radiation, a gravitating mass that is in quadrupole type or higher order vibration, or is asymmetric and in rotation, can emit gravitational waves.[100] These gravitational waves are predicted to travel at the speed of light. For example, planets orbiting the Sun constantly lose energy via gravitational radiation, but this effect is so small that it is unlikely it will be observed in the near future (Earth radiates about 200 watts of gravitational radiation).
The radiation of gravitational waves has been inferred from the Hulse–Taylor binary (and other binary pulsars).[101] Precise timing of the pulses shows that the stars orbit only approximately according to Kepler's Laws: over time they gradually spiral towards each other, demonstrating an energy loss in close agreement with the predicted energy radiated by gravitational waves.[102][103] For their discovery of the first binary pulsar and measuring its orbital decay due to gravitational-wave emission, Hulse and Taylor won the 1993 Nobel Prize in Physics.[104]
A "double pulsar" discovered in 2003, PSR J0737-3039, has a periastron precession of 16.90° per year; unlike the Hulse–Taylor binary, both neutron stars are detected as pulsars, allowing precision timing of both members of the system. Due to this, the tight orbit, the fact that the system is almost edge-on, and the very low transverse velocity of the system as seen from Earth, J0737−3039 provides by far the best system for strong-field tests of general relativity known so far. Several distinct relativistic effects are observed, including orbital decay as in the Hulse–Taylor system. After observing the system for two and a half years, four independent tests of general relativity were possible, the most precise (the Shapiro delay) confirming the general relativity prediction within 0.05%[105] (nevertheless the periastron shift per orbit is only about 0.0013% of a circle and thus it is not a higher-order relativity test).
In 2013, an international team of astronomers reported new data from observing a pulsar-white dwarf system PSR J0348+0432, in which they have been able to measure a change in the orbital period of 8 millionths of a second per year, and confirmed GR predictions in a regime of extreme gravitational fields never probed before;[106] but there are still some competing theories that would agree with these data.[107]
Direct detection of gravitational waves[edit]
A number of gravitational-wave detectors have been built with the intent of directly detecting the gravitational waves emanating from such astronomical events as the merger of two neutron stars or black holes. In February 2016, the Advanced LIGO team announced that they had directly detected gravitational waves from a stellar binary black hole merger,[1][108][109] with additional detections announced in June 2016, June 2017, and August 2017.[2][110]
General relativity predicts gravitational waves, as does any theory of gravitation in which changes in the gravitational field propagate at a finite speed.[111] Then, the LIGO response function could discriminate among the various theories.[112][113] Since gravitational waves can be directly detected,[1][109] it is possible to use them to learn about the Universe. This is gravitational-wave astronomy. Gravitational-wave astronomy can test general relativity by verifying that the observed waves are of the form predicted (for example, that they only have two transverse polarizations), and by checking that black holes are the objects described by solutions of the Einstein field equations.[114][115][116]
Gravitational-wave astronomy can also test Maxwell-Einstein field equations. This version of the field equations predicts that spinning magnetars (i.e., neutron stars with extremely strong magnetic dipole field) should emit gravitational waves.[117]
"These amazing observations are the confirmation of a lot of theoretical work, including Einstein's general theory of relativity, which predicts gravitational waves", said Stephen Hawking.[1]
Direct observation of black holes[edit]

The galaxy M87 was the subject of observation by the Event Horizon Telescope (EHT) in 2017; the 10 April 2019 issue of Astrophysical Journal Letters (vol. 875, No. 1) was dedicated to the EHT results, publishing six open-access papers. The event horizon of the black hole at the center of M87 was directly imaged at the wavelength of radio waves by the EHT; the image was revealed in a press conference on 10 April 2019, the first image of a black hole's event horizon.[119][118] In May 2022, the EHT provided the first image of the super massive black hole Sagittarius A* in the center of our own Milky Way galaxy.
Gravitational redshift and orbit precession of star in strong gravity field[edit]
Gravitational redshift in light from the S2 star orbiting the supermassive black hole Sagittarius A* in the center of the Milky Way has been measured with the Very Large Telescope using GRAVITY, NACO and SIFONI instruments.[120][121] Additionally, there has now been detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole.[122]
Strong equivalence principle[edit]
The strong equivalence principle of general relativity requires universality of free fall to apply even to bodies with strong self-gravity. Direct tests of this principle using Solar System bodies are limited by the weak self-gravity of the bodies, and tests using pulsar–white-dwarf binaries have been limited by the weak gravitational pull of the Milky Way. With the discovery of a triple star system called PSR J0337+1715, located about 4,200 light-years from Earth, the strong equivalence principle can be tested with a high accuracy. This system contains a neutron star in a 1.6-day orbit with a white dwarf star, and the pair in a 327-day orbit with another white dwarf further away. This system permits a test that compares how the gravitational pull of the outer white dwarf affects the pulsar, which has strong self-gravity, and the inner white dwarf. The result shows that the accelerations of the pulsar and its nearby white-dwarf companion differ fractionally by no more than 2.6×10−6 (95% confidence level).[123][124][125]
X-ray spectroscopy[edit]
This technique is based on the idea that photon trajectories are modified in the presence of a gravitational body. A very common astrophysical system in the universe is a black hole surrounded by an accretion disk. The radiation from the general neighborhood, including the accretion disk, is affected by the nature of the central black hole. Assuming Einstein's theory is correct, astrophysical black holes are described by the Kerr metric. (A consequence of the no-hair theorems.) Thus, by analyzing the radiation from such systems, it is possible to test Einstein's theory.
Most of the radiation from these black hole – accretion disk systems (e.g., black hole binaries and active galactic nuclei) arrives in the form of X-rays. When modeled, the radiation is decomposed into several components. Tests of Einstein's theory are possible with the thermal spectrum (only for black hole binaries) and the reflection spectrum (for both black hole binaries and active galactic nuclei). The former is not expected to provide strong constraints,[126] while the latter is much more promising.[127] In both cases, systematic uncertainties might make such tests more challenging.[128]
Cosmological tests[edit]
Tests of general relativity on the largest scales are not nearly so stringent as Solar System tests.[129] The earliest such test was the prediction and discovery of the expansion of the universe.[130] In 1922, Alexander Friedmann found that the Einstein equations have non-stationary solutions (even in the presence of the cosmological constant).[131][132] In 1927, Georges Lemaître showed that static solutions of the Einstein equations, which are possible in the presence of the cosmological constant, are unstable, and therefore the static universe envisioned by Einstein could not exist (it must either expand or contract).[131] Lemaître made an explicit prediction that the universe should expand.[133] He also derived a redshift-distance relationship, which is now known as the Hubble Law.[133] Later, in 1931, Einstein himself agreed with the results of Friedmann and Lemaître.[131] The expansion of the universe discovered by Edwin Hubble in 1929[131] was then considered by many (and continues to be considered by some now) as a direct confirmation of general relativity.[134] In the 1930s, largely due to the work of E. A. Milne, it was realised that the linear relationship between redshift and distance derives from the general assumption of uniformity and isotropy rather than specifically from general relativity.[130] However the prediction of a non-static universe was non-trivial, indeed dramatic, and primarily motivated by general relativity.[135]
Some other cosmological tests include searches for primordial gravitational waves generated during cosmic inflation, which may be detected in the cosmic microwave background polarization[136] or by a proposed space-based gravitational-wave interferometer called the Big Bang Observer. Other tests at high redshift are constraints on other theories of gravity,[137][138] and the variation of the gravitational constant since Big Bang nucleosynthesis (it varied by no more than 40% since then).[citation needed]
In August 2017, the findings of tests conducted by astronomers using the European Southern Observatory's Very Large Telescope (VLT), among other instruments, were released, and positively demonstrated gravitational effects predicted by Albert Einstein. One of these tests observed the orbit of the stars circling around Sagittarius A*, a black hole about 4 million times as massive as the sun. Einstein's theory suggested that large objects bend the space around them, causing other objects to diverge from the straight lines they would otherwise follow. Although previous studies have validated Einstein's theory, this was the first time his theory had been tested on such a gigantic object. The findings were published in The Astrophysical Journal.[139][140]
Gravitational lensing[edit]
Astronomers using the Hubble Space Telescope and the Very Large Telescope have made precise tests of general relativity on galactic scales. The nearby galaxy ESO 325-G004 acts as a strong gravitational lens, distorting light from a distant galaxy behind it to create an Einstein ring around its centre. By comparing the mass of ESO 325-G004 (from measurements of the motions of stars inside this galaxy) with the curvature of space around it, astronomers found that gravity behaves as predicted by general relativity on these astronomical length-scales.[141][142]
See also[edit]
References[edit]
Notes[edit]
- ^ a b c d Castelvecchi, Davide; Witze, Witze (February 11, 2016). "Einstein's gravitational waves found at last". Nature News. doi:10.1038/nature.2016.19361. S2CID 182916902. Retrieved 2016-02-11.
- ^ a b Conover, Emily, LIGO snags another set of gravitational waves, Science News, June 1, 2017. Retrieved 8 June 2017.
- ^ a b Einstein, Albert (1916). "The Foundation of the General Theory of Relativity" (PDF). Annalen der Physik. 49 (7): 769–822. Bibcode:1916AnP...354..769E. doi:10.1002/andp.19163540702. Retrieved 2006-09-03.
- ^ Einstein, Albert (1916). "The Foundation of the General Theory of Relativity" (English HTML, contains link to German PDF). Annalen der Physik. 49 (7): 769–822. Bibcode:1916AnP...354..769E. doi:10.1002/andp.19163540702.
- ^ Einstein, Albert (1919). "What Is The Theory Of Relativity?" (PDF). German History in Documents and Images. Retrieved 7 June 2013.
- ^ "Precession of Mercury's Perihelion" (PDF).
- ^ a b Le Verrier, U. (1859). "Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète". Comptes rendus hebdomadaires des séances de l'Académie des sciences. 49: 379–383.
- ^ Campbell, W. W. (1909). "Report of the Lick Observatory". Publications of the Astronomical Society of the Pacific. 21 (128): 213–214.
- ^ Campbell, W. W. (1908). "The Crocker Eclipse Expedition of 1908 from the Lick Observatory, University of California". Publications of the Astronomical Society of the Pacific. 20 (119): 79. Bibcode:1908PASP...20...63C. doi:10.1086/121793. JSTOR 40692907. S2CID 121157855.
- ^ Baum, Richard; Sheehan, William (1997). In Search of Planet Vulcan: The Ghost in Newton’s Clockwork Universe. Boston, MA: Springer US. doi:10.1007/978-1-4899-6100-6. ISBN 978-0-306-45567-4.
- ^ a b Clemence, G. M. (1947). "The Relativity Effect in Planetary Motions". Reviews of Modern Physics. 19 (4): 361–364. Bibcode:1947RvMP...19..361C. doi:10.1103/RevModPhys.19.361.
- ^ a b Park, Ryan S.; et al. (2017). "Precession of Mercury's Perihelion from Ranging to the MESSENGER Spacecraft". The Astronomical Journal. 153 (3): 121. Bibcode:2017AJ....153..121P. doi:10.3847/1538-3881/aa5be2. hdl:1721.1/109312. S2CID 125439949.
- ^ http://www.tat.physik.uni-tuebingen.de/~kokkotas/Teaching/Experimental_Gravity_files/Hajime_PPN.pdf Archived 2014-03-22 at the Wayback Machine – Perihelion shift of Mercury, page 11
- ^ Dediu, Adrian-Horia; Magdalena, Luis; Martín-Vide, Carlos (2015). Theory and Practice of Natural Computing: Fourth International Conference, TPNC 2015, Mieres, Spain, December 15–16, 2015. Proceedings (illustrated ed.). Springer. p. 141. ISBN 978-3-319-26841-5. Extract of page 141
- ^ Biswas, Abhijit; Mani, Krishnan R. S. (2008). "Relativistic perihelion precession of orbits of Venus and the Earth". Central European Journal of Physics. v1. 6 (3): 754–758. arXiv:0802.0176. Bibcode:2008CEJPh...6..754B. doi:10.2478/s11534-008-0081-6. S2CID 118620173.
- ^ Matzner, Richard Alfred (2001). Dictionary of geophysics, astrophysics, and astronomy. CRC Press. p. 356. Bibcode:2001dgaa.book.....M. ISBN 978-0-8493-2891-6.
- ^ Weisberg, J.M.; Taylor, J.H. (July 2005). "The Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis". Written at San Francisco. In F.A. Rasio; I.H. Stairs (eds.). Binary Radio Pulsars. ASP Conference Series. Vol. 328. Aspen, Colorado, USA: Astronomical Society of the Pacific. p. 25. arXiv:astro-ph/0407149. Bibcode:2005ASPC..328...25W.
- ^ Naeye, Robert, "Stellar Mystery Solved, Einstein Safe", Sky and Telescope, September 16, 2009. See also MIT Press Release, September 17, 2009. Accessed 8 June 2017.
- ^ Soldner, J. G. V. (1804). . Berliner Astronomisches Jahrbuch: 161–172.
- ^ Soares, Domingos S. L. (2009). "Newtonian gravitational deflection of light revisited". arXiv:physics/0508030.
- ^ Will, C.M. (December 2014). "The Confrontation between General Relativity and Experiment". Living Rev. Relativ. 17 (1): 4. arXiv:gr-qc/0510072. Bibcode:2014LRR....17....4W. doi:10.12942/lrr-2014-4. PMC 5255900. PMID 28179848. (ArXiv version here: arxiv.org/abs/1403.7377.)
- ^ Ned Wright: Deflection and Delay of Light
- ^ a b Dyson, F. W.; Eddington, A. S.; Davidson C. (1920). "A determination of the deflection of light by the Sun's gravitational field, from observations made at the total eclipse of 29 May 1919". Philosophical Transactions of the Royal Society. 220A (571–581): 291–333. Bibcode:1920RSPTA.220..291D. doi:10.1098/rsta.1920.0009.
- ^ Stanley, Matthew (2003). "'An Expedition to Heal the Wounds of War': The 1919 Eclipse and Eddington as Quaker Adventurer". Isis. 94 (1): 57–89. Bibcode:2003Isis...94...57S. doi:10.1086/376099. PMID 12725104. S2CID 25615643.
- ^ Rosenthal-Schneider, Ilse: Reality and Scientific Truth. Detroit: Wayne State University Press, 1980. p 74. See also Calaprice, Alice: The New Quotable Einstein. Princeton: Princeton University Press, 2005. p 227.
- ^ Harry Collins and Trevor Pinch, The Golem, ISBN 0-521-47736-0
- ^ Daniel Kennefick (2007). "Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition". Studies in History and Philosophy of Science Part A. 44 (1): 89–101. arXiv:0709.0685. Bibcode:2013SHPSA..44...89S. doi:10.1016/j.shpsa.2012.07.010. S2CID 119203172.
- ^ Ball, Philip (2007). "Arthur Eddington was innocent!". News@nature. doi:10.1038/news070903-20. S2CID 120524925.
- ^ a b D. Kennefick, "Testing relativity from the 1919 eclipse- a question of bias", Physics Today, March 2009, pp. 37–42.
- ^ Barker, Geoff (22 August 2012). "Einstein's Theory of Relativity Proven in Australia, 1922". Museum of Applied Arts and Sciences. Retrieved 20 September 2022.
- ^ van Biesbroeck, G.: The relativity shift at the 1952 February 25 eclipse of the Sun., Astronomical Journal, vol. 58, page 87, 1953.
- ^ Texas Mauritanian Eclipse Team: Gravitational deflection of-light: solar eclipse of 30 June 1973 I. Description of procedures and final results., Astronomical Journal, vol. 81, page 452, 1976.
- ^ Shapiro, Irwin I. (18 August 1967). "New Method for the Detection of Light Deflection by Solar Gravity". Science. 157 (3790): 806–808. Bibcode:1967Sci...157..806S. doi:10.1126/science.157.3790.806. ISSN 0036-8075. PMID 17842783. S2CID 1385516.
- ^ Titov, O.; Girdiuk, A. (2015). Z. Malkin & N. Capitaine (ed.). The deflection of light induced by the Sun's gravitational field and measured with geodetic VLBI. Proceedings of the Journées 2014 "Systèmes de référence spatio-temporels": Recent developments and prospects in ground-based and space astrometry. Pulkovo Observatory, St. Petersburg, Russia. pp. 75–78. arXiv:1502.07395. Bibcode:2015jsrs.conf...75T. ISBN 978-5-9651-0873-2.
- ^ Kailash C. Sahu; Jay Anderson; Stefano Casertano; Howard E. Bond; Pierre Bergeron; Edmund P. Nelan; Laurent Pueyo; Thomas M. Brown; Andrea Bellini; Zoltan G. Levay; Joshua Sokol; Martin Dominik; Annalisa Calamida; Noé Kains; Mario Livio (June 9, 2017). "Relativistic deflection of background starlight measures the mass of a nearby white dwarf star". Science. 356 (6342): 1046–1050. arXiv:1706.02037. Bibcode:2017Sci...356.1046S. doi:10.1126/science.aal2879. hdl:10023/11050. PMID 28592430. S2CID 206654918.
- ^ Hetherington, N. S., "Sirius B and the gravitational redshift – an historical review", Quarterly Journal Royal Astronomical Society, vol. 21, Sept. 1980, p. 246-252. Accessed 6 April 2017.
- ^ a b Holberg, J. B., "Sirius B and the Measurement of the Gravitational Redshift", Journal for the History of Astronomy, Vol. 41, 1, 2010, p. 41-64. Accessed 6 April 2017.
- ^ Effective Temperature, Radius, and Gravitational Redshift of Sirius B, J. L. Greenstein, J.B. Oke, H. L. Shipman, Astrophysical Journal 169 (Nov. 1, 1971), pp. 563–566.
- ^ Dicke, R. H. (March 6, 1959). "New Research on Old Gravitation: Are the observed physical constants independent of the position, epoch, and velocity of the laboratory?". Science. 129 (3349): 621–624. Bibcode:1959Sci...129..621D. doi:10.1126/science.129.3349.621. PMID 17735811.
- ^ Dicke, R. H. (1962). "Mach's Principle and Equivalence". Evidence for gravitational theories: proceedings of course 20 of the International School of Physics "Enrico Fermi" ed C. Møller.
- ^ Schiff, L. I. (April 1, 1960). "On Experimental Tests of the General Theory of Relativity". American Journal of Physics. 28 (4): 340–343. Bibcode:1960AmJPh..28..340S. doi:10.1119/1.1935800.
- ^ Brans, C. H.; Dicke, R. H. (November 1, 1961). "Mach's Principle and a Relativistic Theory of Gravitation". Physical Review. 124 (3): 925–935. Bibcode:1961PhRv..124..925B. doi:10.1103/PhysRev.124.925.
- ^ "Fact Sheet".
- ^ Milani, Andrea; Vokrouhlický, David; Villani, Daniela; Bonanno, Claudio; Rossi, Alessandro (2002). "Testing general relativity with the BepiColombo radio science experiment". Physical Review D. 66 (8): 082001. Bibcode:2002PhRvD..66h2001M. doi:10.1103/PhysRevD.66.082001.
- ^ Schettino, Giulia; Tommei, Giacomo (2016). "Testing General Relativity with the Radio Science Experiment of the BepiColombo mission to Mercury". Universe. 2 (3): 21. Bibcode:2016Univ....2...21S. doi:10.3390/universe2030021. hdl:11568/804045.
- ^ The Mercury Orbiter Radio Science Experiment (MORE) on board the ESA/JAXA BepiColombo MIssion to Mercury. SERRA, DANIELE; TOMMEI, GIACOMO; MILANI COMPARETTI, ANDREA. Università di Pisa, 2017.
- ^ Fomalont, E.B.; Kopeikin S.M.; Lanyi, G.; Benson, J. (July 2009). "Progress in Measurements of the Gravitational Bending of Radio Waves Using the VLBA". Astrophysical Journal. 699 (2): 1395–1402. arXiv:0904.3992. Bibcode:2009ApJ...699.1395F. doi:10.1088/0004-637X/699/2/1395. S2CID 4506243.
- ^ esa. "Gaia overview".
- ^ Shapiro, I. I. (December 28, 1964). "Fourth test of general relativity". Physical Review Letters. 13 (26): 789–791. Bibcode:1964PhRvL..13..789S. doi:10.1103/PhysRevLett.13.789.
- ^ Shapiro, I. I.; Ash M. E.; Ingalls R. P.; Smith W. B.; Campbell D. B.; Dyce R. B.; Jurgens R. F. & Pettengill G. H. (May 3, 1971). "Fourth Test of General Relativity: New Radar Result". Physical Review Letters. 26 (18): 1132–1135. Bibcode:1971PhRvL..26.1132S. doi:10.1103/PhysRevLett.26.1132.
- ^ Bertotti B.; Iess L.; Tortora P. (2003). "A test of general relativity using radio links with the Cassini spacecraft". Nature. 425 (6956): 374–376. Bibcode:2003Natur.425..374B. doi:10.1038/nature01997. PMID 14508481. S2CID 4337125.
- ^ Kopeikin S.~M.; Polnarev A.~G.; Schaefer G.; Vlasov I.Yu. (2007). "Gravimagnetic effect of the barycentric motion of the Sun and determination of the post-Newtonian parameter γ in the Cassini experiment". Physics Letters A. 367 (4–5): 276–280. arXiv:gr-qc/0604060. Bibcode:2007PhLA..367..276K. doi:10.1016/j.physleta.2007.03.036. S2CID 18890863.
- ^ Kopeikin S.~M. (2009). "Post-Newtonian limitations on measurement of the PPN parameters caused by motion of gravitating bodies". Monthly Notices of the Royal Astronomical Society. 399 (3): 1539–1552. arXiv:0809.3433. Bibcode:2009MNRAS.399.1539K. doi:10.1111/j.1365-2966.2009.15387.x. S2CID 10506077.
- ^ Fomalont, E.B.; Kopeikin S.M. (November 2003). "The Measurement of the Light Deflection from Jupiter: Experimental Results". Astrophysical Journal. 598 (1): 704–711. arXiv:astro-ph/0302294. Bibcode:2003ApJ...598..704F. doi:10.1086/378785. S2CID 14002701.
- ^ Kopeikin, S.M.; Fomalont E.B. (October 2007). "Gravimagnetism, causality, and aberration of gravity in the gravitational light-ray deflection experiments". General Relativity and Gravitation. 39 (10): 1583–1624. arXiv:gr-qc/0510077. Bibcode:2007GReGr..39.1583K. doi:10.1007/s10714-007-0483-6. S2CID 15412146.
- ^ Fomalont, E.B.; Kopeikin, S. M.; Jones, D.; Honma, M.; Titov, O. (January 2010). "Recent VLBA/VERA/IVS tests of general relativity". Proceedings of the International Astronomical Union, IAU Symposium. 261 (S261): 291–295. arXiv:0912.3421. Bibcode:2010IAUS..261..291F. doi:10.1017/S1743921309990536. S2CID 9146534.
- ^ Nordtvedt, K. Jr. (May 25, 1968). "Equivalence Principle for Massive Bodies. II. Theory". Physical Review. 169 (5): 1017–1025. Bibcode:1968PhRv..169.1017N. doi:10.1103/PhysRev.169.1017.
- ^ Nordtvedt, K. Jr. (June 25, 1968). "Testing Relativity with Laser Ranging to the Moon". Physical Review. 170 (5): 1186–1187. Bibcode:1968PhRv..170.1186N. doi:10.1103/PhysRev.170.1186.
- ^ Williams, J. G.; Turyshev, Slava G.; Boggs, Dale H. (December 29, 2004). "Progress in Lunar Laser Ranging Tests of Relativistic Gravity". Physical Review Letters. 93 (5): 1017–1025. arXiv:gr-qc/0411113. Bibcode:2004PhRvL..93z1101W. doi:10.1103/PhysRevLett.93.261101. PMID 15697965. S2CID 119358769.
- ^ Uzan, J. P. (2003). "The fundamental constants and their variation: Observational status and theoretical motivations". Reviews of Modern Physics. 75 (5): 403–. arXiv:hep-ph/0205340. Bibcode:2003RvMP...75..403U. doi:10.1103/RevModPhys.75.403. S2CID 118684485.
- ^ Pound, R. V.; Rebka, G. A. Jr. (November 1, 1959). "Gravitational Red-Shift in Nuclear Resonance". Physical Review Letters. 3 (9): 439–441. Bibcode:1959PhRvL...3..439P. doi:10.1103/PhysRevLett.3.439.
- ^ Pound, R. V.; Rebka, G. A. Jr. (April 1, 1960). "Apparent weight of photons". Physical Review Letters. 4 (7): 337–341. Bibcode:1960PhRvL...4..337P. doi:10.1103/PhysRevLett.4.337.
- ^ Pound, R. V.; Snider J. L. (November 2, 1964). "Effect of Gravity on Nuclear Resonance". Physical Review Letters. 13 (18): 539–540. Bibcode:1964PhRvL..13..539P. doi:10.1103/PhysRevLett.13.539.
- ^ Vessot, R. F. C.; M. W. Levine; E. M. Mattison; E. L. Blomberg; T. E. Hoffman; G. U. Nystrom; B. F. Farrel; R. Decher; et al. (December 29, 1980). "Test of Relativistic Gravitation with a Space-Borne Hydrogen Maser". Physical Review Letters. 45 (26): 2081–2084. Bibcode:1980PhRvL..45.2081V. doi:10.1103/PhysRevLett.45.2081.
- ^ Neil, Ashby (28 January 2003). "Relativity in the Global Positioning System". Living Reviews in Relativity. 6 (1): 1. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. PMC 5253894. PMID 28163638.
- ^ "Gravitational Physics with Optical Clocks in Space" (PDF). S. Schiller (PDF). Heinrich Heine Universität Düsseldorf. 2007. Retrieved 19 March 2015.
- ^ Hafele, J. C.; Keating, R. E. (July 14, 1972). "Around-the-World Atomic Clocks: Predicted Relativistic Time Gains". Science. 177 (4044): 166–168. Bibcode:1972Sci...177..166H. doi:10.1126/science.177.4044.166. PMID 17779917. S2CID 10067969.
- ^ Hafele, J. C.; Keating, R. E. (July 14, 1972). "Around-the-World Atomic Clocks: Observed Relativistic Time Gains". Science. 177 (4044): 168–170. Bibcode:1972Sci...177..168H. doi:10.1126/science.177.4044.168. PMID 17779918. S2CID 37376002.
- ^ Ciufolini I. & Pavlis E.C. (2004). "A confirmation of the general relativistic prediction of the Lense–Thirring effect". Nature. 431 (7011): 958–960. Bibcode:2004Natur.431..958C. doi:10.1038/nature03007. PMID 15496915. S2CID 4423434.
- ^ Krogh K. (2007). "Comment on 'Evidence of the gravitomagnetic field of Mars'". Classical and Quantum Gravity. 24 (22): 5709–5715. arXiv:astro-ph/0701653. Bibcode:2007CQGra..24.5709K. doi:10.1088/0264-9381/24/22/N01. S2CID 12238950.
- ^ Merritt, D.; Alexander, T.; Mikkola, S.; Will, C. (2010). "Testing Properties of the Galactic Center Black Hole Using Stellar Orbits". Physical Review D. 81 (6): 062002. arXiv:0911.4718. Bibcode:2010PhRvD..81f2002M. doi:10.1103/PhysRevD.81.062002. S2CID 118646069.
- ^ Will, C. (2008). "Testing the General Relativistic "No-Hair" Theorems Using the Galactic Center Black Hole Sagittarius A*". Astrophysical Journal Letters. 674 (1): L25–L28. arXiv:0711.1677. Bibcode:2008ApJ...674L..25W. doi:10.1086/528847. S2CID 11685632.
- ^ Everitt; et al. (2011). "Gravity Probe B: Final Results of a Space Experiment to Test General Relativity". Physical Review Letters. 106 (22): 221101. arXiv:1105.3456. Bibcode:2011PhRvL.106v1101E. doi:10.1103/PhysRevLett.106.221101. PMID 21702590. S2CID 11878715.
- ^ Ker Than (2011-05-05). "Einstein Theories Confirmed by NASA Gravity Probe". News.nationalgeographic.com. Archived from the original on May 7, 2011. Retrieved 2011-05-08.
- ^ "Prepping satellite to test Albert Einstein".
- ^ Ciufolini, I.; et al. (2009). "Towards a One Percent Measurement of Frame Dragging by Spin with Satellite Laser Ranging to LAGEOS, LAGEOS 2 and LARES and GRACE Gravity Models". Space Science Reviews. 148 (1–4): 71–104. Bibcode:2009SSRv..148...71C. doi:10.1007/s11214-009-9585-7. S2CID 120442993.
- ^ Ciufolini, I.; Paolozzi A.; Pavlis E. C.; Ries J. C.; Koenig R.; Matzner R. A.; Sindoni G. & Neumayer H. (2009). "Towards a One Percent Measurement of Frame Dragging by Spin with Satellite Laser Ranging to LAGEOS, LAGEOS 2 and LARES and GRACE Gravity Models". Space Science Reviews. 148 (1–4): 71–104. Bibcode:2009SSRv..148...71C. doi:10.1007/s11214-009-9585-7. S2CID 120442993.
- ^ Ciufolini, I.; Paolozzi A.; Pavlis E. C.; Ries J. C.; Koenig R.; Matzner R. A.; Sindoni G. & Neumayer H. (2010). "Gravitomagnetism and Its Measurement with Laser Ranging to the LAGEOS Satellites and GRACE Earth Gravity Models". General Relativity and John Archibald Wheeler. Astrophysics and Space Science Library. Vol. 367. SpringerLink. pp. 371–434. doi:10.1007/978-90-481-3735-0_17. ISBN 978-90-481-3734-3.
- ^ Paolozzi, A.; Ciufolini I.; Vendittozzi C. (2011). "Engineering and scientific aspects of LARES satellite". Acta Astronautica. 69 (3–4): 127–134. Bibcode:2011AcAau..69..127P. doi:10.1016/j.actaastro.2011.03.005. ISSN 0094-5765.
- ^ Kapner; Adelberger (8 January 2007). "Tests of the Gravitational Inverse-Square Law below the Dark-Energy Length Scale". Physical Review Letters. 98 (2): 021101. arXiv:hep-ph/0611184. Bibcode:2007PhRvL..98b1101K. doi:10.1103/PhysRevLett.98.021101. PMID 17358595. S2CID 16379220.
- ^ Miller, A I (1997-01-01). "The Collected Papers of Albert Einstein; Volume 6 The Berlin Years: Writings 1914 – 1917". European Journal of Physics. 18 (1). doi:10.1088/0143-0807/18/1/012. ISSN 0143-0807. S2CID 250837656.
- ^ Hay, H.J.; Schiffer, J.P.; Cranshaw, T.E.; Egelstaff, P.A. (1960-02-15). "Measurement of the Red Shift in an Accelerated System Using the Mössbauer Effect in ${\mathrm{Fe}}^{57}$". Physical Review Letters. 4 (4): 165–166. doi:10.1103/PhysRevLett.4.165.
- ^ Champeney, D.C.; Isaak, G.R.; Khan, A.M. (March 1965). "A time dilatation experiment based on the Mössbauer effect". Proceedings of the Physical Society. 85 (3): 583–593. Bibcode:1965PPS....85..583C. doi:10.1088/0370-1328/85/3/317. ISSN 0370-1328.
- ^ Kündig, W. (1963-03-15). "Measurement of the Transverse Doppler Effect in an Accelerated System". Physical Review. 129 (6): 2371–2375. Bibcode:1963PhRv..129.2371K. doi:10.1103/PhysRev.129.2371.
- ^ Kholmetskii, A.L.; Yarman, T.; Missevitch, O.V. (2008-02-06). "Kündig's experiment on the transverse Doppler shift re-analyzed". Physica Scripta. 77 (3): 035302. Bibcode:2008PhyS...77c5302K. doi:10.1088/0031-8949/77/03/035302. S2CID 30608323.
- ^ Kholmetskii, A.L.; Yarman, T.; Missevitch, O.V.; Rogozev, B.I. (2009-05-27). "A Mössbauer experiment in a rotating system on the second-order Doppler shift: confirmation of the corrected result by Kündig". Physica Scripta. 79 (6): 065007. Bibcode:2009PhyS...79f5007K. doi:10.1088/0031-8949/79/06/065007. ISSN 0031-8949. S2CID 121546571.
- ^ Kholmetskii, A.L.; Yarman, T.; Missevitch, O.V. (2009-08-20). "Moessbauer experiment in a rotating system: The change of time rate for resonant nuclei due to the motion and interaction energy". Il Nuovo Cimento B. 124 (8): 791–803. doi:10.1393/ncb/i2010-10808-4.
- ^ Yarman, T.; Kholmetskii, A.L.; Arik, M.; Akkus, B.; Oktem, Y.; Susam, L.A.; Missevitch, O.V. (2016-08-10). "Novel Mössbauer experiment in a rotating system and the extra-energy shift between emission and absorption lines". Canadian Journal of Physics. 94 (8): 780–789. arXiv:1503.05853. Bibcode:2016CaJPh..94..780Y. doi:10.1139/cjp-2015-0063. S2CID 117936697.
- ^ Kholmetskii, A.L.; Yarman, T.; Missevitch, O.V. (2013-04-04). "Mössbauer effect in rotating systems: possible explanation of the extra energy shift". The European Physical Journal Plus. 128 (4): 42. Bibcode:2013EPJP..128...42K. doi:10.1140/epjp/i2013-13042-0. S2CID 120671970.
- ^ Corda, C. (2015-04-20). "Interpretation of Mössbauer experiment in a rotating system: A new proof for general relativity". Annals of Physics. 355: 360–366. arXiv:1502.04911. Bibcode:2015AnPhy.355..360C. doi:10.1016/j.aop.2015.02.021. S2CID 119248058.
- ^ Corda, C. (2016-05-20). "The Mössbauer rotor experiment and the general theory of relativity". Annals of Physics. 368: 258–266. arXiv:1602.04212. Bibcode:2016AnPhy.368..258C. doi:10.1016/j.aop.2016.02.011. S2CID 55583610.
- ^ Corda, C. (2018-09-30). "New proof of general relativity through the correct physical interpretation of the Mössbauer rotor experiment". International Journal of Modern Physics D. 27 (14): 1847016. arXiv:1805.06228. Bibcode:2018IJMPD..2747016C. doi:10.1142/S0218271818470168. ISSN 0218-2718. S2CID 56302187.
- ^ Corda, C. (2019-07-20). "Mössbauer rotor experiment as new proof of general relativity: Rigorous computation of the additional effect of clock synchronization". International Journal of Modern Physics D. 28 (10): 1950131. arXiv:1904.13252. Bibcode:2019IJMPD..2850131C. doi:10.1142/S0218271819501311. ISSN 0218-2718. S2CID 145981014.
- ^ Kholmetskii, A.L.; Yarman, T.; Arik, M. (2015-01-10). "Comment on "Interpretation of Mössbauer experiment in a rotating system: A new proof by general relativity"". Annals of Physics. 363: 556–558. Bibcode:2015AnPhy.363..556K. doi:10.1016/j.aop.2015.09.007.
- ^ Yarman, T.; Kholmetskii, A.L.; Arik, M. (2015-10-10). "Mössbauer experiments in a rotating system: Recent errors and novel interpretation". The European Physical Journal Plus. 130 (10): 191. Bibcode:2015EPJP..130..191Y. doi:10.1140/epjp/i2015-15191-4. S2CID 124589281.
- ^ Kholmetskii, A.L.; Yarman, T.; Yarman, O.; Arik, M. (2016-11-10). "Response to "The Mössbauer rotor experiment and the general theory of relativity" by C. Corda". Annals of Physics. 374: 247–254. arXiv:1610.04219. Bibcode:2016AnPhy.374..247K. doi:10.1016/j.aop.2016.08.016.
- ^ Kholmetskii, A.L.; Yarman, T.; Yarman, O.; Arik, M. (2018-11-14). "Einstein's "Clock Hypothesis" and Mössbauer Experiments in a Rotating System". Zeitschrift für Naturforschung A. 74 (2): 91. doi:10.1515/zna-2018-0354. S2CID 105930092.
- ^ Kholmetskii, A.L.; Yarman, T.; Yarman, O.; Arik, M. (2019-05-20). "Comment on "New proof of general relativity through the correct physical interpretation of the Mössbauer rotor experiment" by C. Corda". International Journal of Modern Physics D. 28 (10): 1950127. arXiv:1906.12161. Bibcode:2019IJMPD..2850127K. doi:10.1142/S021827181950127X. S2CID 149746550.
- ^ Kholmetskii, A.L.; Yarman, T.; Yarman, O.; Arik, M. (2019-10-10). "On the synchronization of a clock at the origin of a rotating system with a laboratory clock in Mössbauer rotor experiments". Annals of Physics. 409 (10): 167931. arXiv:1906.12161. Bibcode:2019IJMPD..2850127K. doi:10.1142/S021827181950127X. S2CID 149746550.
- ^ In general relativity, a perfectly spherical star (in vacuum) that expands or contracts while remaining perfectly spherical cannot emit any gravitational waves (similar to the lack of e/m radiation from a pulsating charge), as Birkhoff's theorem says that the geometry remains the same exterior to the star. More generally, a rotating system will only emit gravitational waves if it lacks the axial symmetry with respect to the axis of rotation.
- ^ Stairs, Ingrid H. (2003). "Testing General Relativity with Pulsar Timing". Living Reviews in Relativity. 6 (1): 5. arXiv:astro-ph/0307536. Bibcode:2003LRR.....6....5S. doi:10.12942/lrr-2003-5. PMC 5253800. PMID 28163640.
- ^ Weisberg, J. M.; Taylor, J. H.; Fowler, L. A. (October 1981). "Gravitational waves from an orbiting pulsar". Scientific American. 245 (4): 74–82. Bibcode:1981SciAm.245d..74W. doi:10.1038/scientificamerican1081-74.
- ^ Weisberg, J. M.; Nice, D. J.; Taylor, J. H. (2010). "Timing Measurements of the Relativistic Binary Pulsar PSR B1913+16". Astrophysical Journal. 722 (2): 1030–1034. arXiv:1011.0718. Bibcode:2010ApJ...722.1030W. doi:10.1088/0004-637X/722/2/1030. S2CID 118573183.
- ^ "Press Release: The Nobel Prize in Physics 1993". Nobel Prize. 13 October 1993. Retrieved 6 May 2014.
- ^ Kramer, M.; et al. (2006). "Tests of general relativity from timing the double pulsar". Science. 314 (5796): 97–102. arXiv:astro-ph/0609417. Bibcode:2006Sci...314...97K. doi:10.1126/science.1132305. PMID 16973838. S2CID 6674714.
- ^ Antoniadis, John; et al. (2013). "A Massive Pulsar in a Compact Relativistic Binary". Science. 340 (6131): 1233232. arXiv:1304.6875. Bibcode:2013Sci...340..448A. doi:10.1126/science.1233232. PMID 23620056. S2CID 15221098.
- ^ Cowen, Ron (25 April 2013). "Massive double star is latest test for Einstein's gravity theory". Nature. doi:10.1038/nature.2013.12880. S2CID 123752543. Retrieved 7 May 2013.
- ^ B. P. Abbott; et al. (2016). "Observation of Gravitational Waves from a Binary Black Hole Merger". Physical Review Letters. 116 (6): 061102. arXiv:1602.03837. Bibcode:2016PhRvL.116f1102A. doi:10.1103/PhysRevLett.116.061102. PMID 26918975. S2CID 124959784.
- ^ a b "Gravitational waves detected 100 years after Einstein's prediction | NSF - National Science Foundation". www.nsf.gov. Retrieved 2016-02-11.
- ^ Choi, Charles Q. (16 October 2017). "Gravitational Waves Detected from Neutron-Star Crashes: The Discovery Explained". Space.com. Purch. Retrieved 1 November 2017.
- ^ Schutz, Bernard F. (1984). "Gravitational waves on the back of an envelope" (PDF). American Journal of Physics. 52 (5): 412–419. Bibcode:1984AmJPh..52..412S. doi:10.1119/1.13627. hdl:11858/00-001M-0000-0013-747D-5.
- ^ R., Saulson, Peter (1994). Fundamentals of interferometric gravitational wave detectors. World scientific. ISBN 981-02-1820-6. OCLC 799449990.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Corda, Christian (2009-12-31). "Interferometric detection of gravitational waves: the definitive test for general relativity". International Journal of Modern Physics D. 18 (14): 2275–2282. arXiv:0905.2502. Bibcode:2009IJMPD..18.2275C. doi:10.1142/S0218271809015904. ISSN 0218-2718. S2CID 721314.
- ^ Gair, Jonathan; Vallisneri, Michele; Larson, Shane L.; Baker, John G. (2013). "Testing General Relativity with Low-Frequency, Space-Based Gravitational-Wave Detectors". Living Reviews in Relativity. 16 (1): 7. arXiv:1212.5575. Bibcode:2013LRR....16....7G. doi:10.12942/lrr-2013-7. PMC 5255528. PMID 28163624.
- ^ Yunes, Nicolás; Siemens, Xavier (2013). "Gravitational-Wave Tests of General Relativity with Ground-Based Detectors and Pulsar-Timing Arrays". Living Reviews in Relativity. 16 (1): 9. arXiv:1304.3473. Bibcode:2013LRR....16....9Y. doi:10.12942/lrr-2013-9. PMC 5255575. PMID 28179845.
- ^ Abbott, Benjamin P.; et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016). "Tests of general relativity with GW150914". Physical Review Letters. 116 (221101): 221101. arXiv:1602.03841. Bibcode:2016PhRvL.116v1101A. doi:10.1103/PhysRevLett.116.221101. PMID 27314708. S2CID 217275338.
- ^ Corsi, A.; Meszaros, P. (8 Nov 2018). "GRB Afterglow Plateaus and gravitational waves: multi-messenger signature of a millisecond Magnetar?". Astrophys. J. 702: 1171–1178. arXiv:0907.2290. doi:10.1088/0004-637X/702/2/1171. S2CID 16723637.
- ^ a b The Event Horizon Telescope Collaboration (2019). "First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole". The Astrophysical Journal. 875 (1): L1. arXiv:1906.11238. Bibcode:2019ApJ...875L...1E. doi:10.3847/2041-8213/ab0ec7. S2CID 145906806.
- ^ "Focus on the First Event Horizon Telescope Results". Shep Doeleman. The Astrophysical Journal. 10 April 2019. Retrieved 14 April 2019.
- ^ "First Successful Test of Einstein's General Relativity Near Supermassive Black Hole". Hämmerle, Hannelore. Max Planck Institute for Extraterrestrial Physics. 26 July 2018. Retrieved 28 July 2018.
- ^ GRAVITY Collaboration (26 July 2018). "Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole". Astronomy & Astrophysics. 615 (L15): L15. arXiv:1807.09409. Bibcode:2018A&A...615L..15G. doi:10.1051/0004-6361/201833718. S2CID 118891445.
- ^ GRAVITY Collaboration (16 April 2020). "Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole". Astronomy & Astrophysics. 636 (L5): L5. arXiv:2004.07187. Bibcode:2020A&A...636L...5G. doi:10.1051/0004-6361/202037813. S2CID 215768928.
- ^ Anne M. Archibald; et al. (4 July 2018). "Universality of free fall from the orbital motion of a pulsar in a stellar triple system". Nature. 559 (7712): 73–76. arXiv:1807.02059. Bibcode:2018Natur.559...73A. doi:10.1038/s41586-018-0265-1. PMID 29973733. S2CID 49578025.
- ^ "Even Phenomenally Dense Neutron Stars Fall like a Feather - Einstein Gets It Right Again". Charles Blue, Paul Vosteen. NRAO. 4 July 2018. Retrieved 28 July 2018.
- ^ Voisin, G.; Cognard, I.; Freire, P. C. C.; Wex, N.; Guillemot, L.; Desvignes, G.; Kramer, M.; Theureau, G. (2020-06-01). "An improved test of the strong equivalence principle with the pulsar in a triple star system". Astronomy & Astrophysics. 638: A24. arXiv:2005.01388. Bibcode:2020A&A...638A..24V. doi:10.1051/0004-6361/202038104. ISSN 0004-6361. S2CID 218486794.
- ^ Kong, Lingyao; Li, Zilong; Bambi, Cosimo (2014). "Constraints on the Spacetime Geometry around 10 Stellar-mass Black Hole Candidates from the Disk's Thermal Spectrum". The Astrophysical Journal. 797 (2): 78. arXiv:1405.1508. Bibcode:2014ApJ...797...78K. doi:10.1088/0004-637X/797/2/78. ISSN 0004-637X. S2CID 119280889.
- ^ Bambi, Cosimo (2017-04-06). "Testing black hole candidates with electromagnetic radiation". Reviews of Modern Physics. 89 (2): 025001. arXiv:1509.03884. Bibcode:2017RvMP...89b5001B. doi:10.1103/RevModPhys.89.025001. S2CID 118397255.
- ^ Krawczynski, Henric (2018-07-24). "Difficulties of quantitative tests of the Kerr-hypothesis with X-ray observations of mass accreting black holes". General Relativity and Gravitation. 50 (8): 100. arXiv:1806.10347. Bibcode:2018GReGr..50..100K. doi:10.1007/s10714-018-2419-8. ISSN 0001-7701. S2CID 119372075.
- ^ Peebles, P. J. E. (December 2004). "Probing General Relativity on the Scales of Cosmology". General Relativity and Gravitation. pp. 106–117. arXiv:astro-ph/0410284. Bibcode:2005grg..conf..106P. doi:10.1142/9789812701688_0010. ISBN 978-981-256-424-5. S2CID 1700265.
- ^ a b Rudnicki, 1991, p. 28. The Hubble Law was viewed by many as an observational confirmation of General Relativity in the early years
- ^ a b c d W.Pauli, 1958, pp. 219–220
- ^ Kragh, 2003, p. 152
- ^ a b Kragh, 2003, p. 153
- ^ Rudnicki, 1991, p. 28
- ^ Chandrasekhar, 1980, p. 37
- ^ Hand, Eric (2009). "Cosmology: The test of inflation". Nature. 458 (7240): 820–824. doi:10.1038/458820a. PMID 19370005.
- ^ Reyes, Reinabelle; et al. (2010). "Confirmation of general relativity on large scales from weak lensing and galaxy velocities". Nature. 464 (7286): 256–258. arXiv:1003.2185. Bibcode:2010Natur.464..256R. doi:10.1038/nature08857. PMID 20220843. S2CID 205219902.
- ^ Guzzo, L.; et al. (2008). "A test of the nature of cosmic acceleration using galaxy redshift distortions". Nature. 451 (7178): 541–544. arXiv:0802.1944. Bibcode:2008Natur.451..541G. doi:10.1038/nature06555. PMID 18235494. S2CID 4403989.
- ^ Patel, Neel V. (9 August 2017). "The Milky Way's Supermassive Black Hole is Proving Einstein Correct". Inverse via Yahoo.news. Retrieved 9 August 2017.
- ^ Duffy, Sean (10 August 2017). "Black Hole Indicates Einstein Was Right: Gravity Bends Space". Courthouse News Service. Retrieved 10 August 2017.
- ^ "Einstein proved right in another galaxy". Press Office. University of Portsmouth. 22 June 2018. Retrieved 28 July 2018.
- ^ Thomas E. Collett; et al. (22 June 2018). "A precise extragalactic test of General Relativity". Science. 360 (6395): 1342–1346. arXiv:1806.08300. Bibcode:2018Sci...360.1342C. doi:10.1126/science.aao2469. PMID 29930135. S2CID 49363216.
Other research papers[edit]
- Bertotti, B.; Iess, L.; Tortora, P. (2003). "A test of general relativity using radio links with the Cassini spacecraft". Nature. 425 (6956): 374–6. Bibcode:2003Natur.425..374B. doi:10.1038/nature01997. PMID 14508481. S2CID 4337125.
- Kopeikin, S.; Polnarev, A.; Schaefer, G.; Vlasov, I. (2007). "Gravimagnetic effect of the barycentric motion of the Sun and determination of the post-Newtonian parameter γ in the Cassini experiment". Physics Letters A. 367 (4–5): 276–280. arXiv:gr-qc/0604060. Bibcode:2007PhLA..367..276K. doi:10.1016/j.physleta.2007.03.036. S2CID 18890863.
- Brans, C.; Dicke, R. H. (1961). "Mach's principle and a relativistic theory of gravitation". Phys. Rev. 124 (3): 925–35. Bibcode:1961PhRv..124..925B. doi:10.1103/PhysRev.124.925.
- A. Einstein, "Über das Relativitätsprinzip und die aus demselben gezogene Folgerungen", Jahrbuch der Radioaktivitaet und Elektronik 4 (1907); translated "On the relativity principle and the conclusions drawn from it", in The collected papers of Albert Einstein. Vol. 2 : The Swiss years: writings, 1900–1909 (Princeton University Press, Princeton, New Jersey, 1989), Anna Beck translator. Einstein proposes the gravitational redshift of light in this paper, discussed online at The Genesis of General Relativity.
- A. Einstein, "Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes", Annalen der Physik 35 (1911); translated "On the Influence of Gravitation on the Propagation of Light" in The collected papers of Albert Einstein. Vol. 3 : The Swiss years: writings, 1909–1911 (Princeton University Press, Princeton, New Jersey, 1994), Anna Beck translator, and in The Principle of Relativity, (Dover, 1924), pp 99–108, W. Perrett and G. B. Jeffery translators, ISBN 0-486-60081-5. The deflection of light by the sun is predicted from the principle of equivalence. Einstein's result is half the full value found using the general theory of relativity.
- Shapiro, S. S.; Davis, J. L.; Lebach, D. E.; Gregory J.S. (26 March 2004). "Measurement of the solar gravitational deflection of radio waves using geodetic very-long-baseline interferometry data, 1979–1999". Physical Review Letters. 92 (121101): 121101. Bibcode:2004PhRvL..92l1101S. doi:10.1103/PhysRevLett.92.121101. PMID 15089661.
- M. Froeschlé, F. Mignard and F. Arenou, "Determination of the PPN parameter γ with the Hipparcos data" Hipparcos Venice '97, ESA-SP-402 (1997).
- Will, Clifford M. (2006). "Was Einstein Right? Testing Relativity at the Centenary". Annalen der Physik. 15 (1–2): 19–33. arXiv:gr-qc/0504086. Bibcode:2006AnP...518...19W. doi:10.1002/andp.200510170. S2CID 117829175.
- Rudnicki, Conrad (1991). "What are the Empirical Bases of the Hubble Law" (PDF). Apeiron (9–10): 27–36. Retrieved 2009-06-23.
- Chandrasekhar, S. (1980). "The Role of General Relativity in Astronomy: Retrospect and Prospect" (PDF). J. Astrophys. Astron. 1 (1): 33–45. Bibcode:1980JApA....1...33C. doi:10.1007/BF02727948. S2CID 125915338. Retrieved 2009-06-23.
- Kragh, Helge; Smith, Robert W. (2003). "Who discovered the expanding universe". History of Science. 41 (2): 141–62. Bibcode:2003HisSc..41..141K. doi:10.1177/007327530304100202. S2CID 119368912.
Textbooks[edit]
- S. M. Carroll, Spacetime and Geometry: an Introduction to General Relativity, Addison-Wesley, 2003. A graduate-level general relativity textbook.
- A. S. Eddington, Space, Time and Gravitation, Cambridge University Press, reprint of 1920 ed.
- A. Gefter, "Putting Einstein to the Test", Sky and Telescope July 2005, p. 38. A popular discussion of tests of general relativity.
- H. Ohanian and R. Ruffini, Gravitation and Spacetime, 2nd Edition Norton, New York, 1994, ISBN 0-393-96501-5. A general relativity textbook.
- Pauli, Wolfgang Ernst (1958). "Part IV. General Theory of Relativity". Theory of Relativity. Courier Dover Publications. ISBN 978-0-486-64152-2.
- C. M. Will, Theory and Experiment in Gravitational Physics, Cambridge University Press, Cambridge (1993). A standard technical reference.
- C. M. Will, Was Einstein Right?: Putting General Relativity to the Test, Basic Books (1993). This is a popular account of tests of general relativity.
Living Reviews papers[edit]
- Ashby, Neil (2003). "Relativity in the Global Positioning System". Living Reviews in Relativity. 6 (1): 1. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. PMC 5253894. PMID 28163638. S2CID 12506785.
- Will, Clifford M. (2014). "The Confrontation between General Relativity and Experiment". Living Reviews in Relativity. 17 (1): 4. arXiv:1403.7377. Bibcode:2014LRR....17....4W. doi:10.12942/lrr-2014-4. PMC 5255900. PMID 28179848. An online, technical review, covering much of the material in Theory and experiment in gravitational physics. It is less comprehensive but more up to date.
External links[edit]
- the USENET Relativity FAQ experiments page
- Mathpages article on Mercury's perihelion shift (for amount of observed and GR shifts).






