Collection of proofs of equations involving trigonometric functions
There are several equivalent ways for defining trigonometric functions , and the proofs of the trigonometric identities between them depend on the chosen definition. The oldest and most elementary definitions are based on the geometry of right triangles . The proofs given in this article use these definitions, and thus apply to non-negative angles not greater than a right angle . For greater and negative angles , see Trigonometric functions .
Other definitions, and therefore other proofs are based on the Taylor series of sine and cosine , or on the differential equation
f
″
+
f
=
0
{\displaystyle f''+f=0}
Elementary trigonometric identities [ edit ] Definitions [ edit ] Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle. For example, the sine of angle θ is defined as being the length of the opposite side divided by the length of the hypotenuse. The six trigonometric functions are defined for every real number , except, for some of them, for angles that differ from 0 by a multiple of the right angle (90°). Referring to the diagram at the right, the six trigonometric functions of θ are, for angles smaller than the right angle:
sin
θ
=
o
p
p
o
s
i
t
e
h
y
p
o
t
e
n
u
s
e
=
a
h
{\displaystyle \sin \theta ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}={\frac {a}{h}}}
cos
θ
=
a
d
j
a
c
e
n
t
h
y
p
o
t
e
n
u
s
e
=
b
h
{\displaystyle \cos \theta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}={\frac {b}{h}}}
tan
θ
=
o
p
p
o
s
i
t
e
a
d
j
a
c
e
n
t
=
a
b
{\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {a}{b}}}
cot
θ
=
a
d
j
a
c
e
n
t
o
p
p
o
s
i
t
e
=
b
a
{\displaystyle \cot \theta ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}={\frac {b}{a}}}
sec
θ
=
h
y
p
o
t
e
n
u
s
e
a
d
j
a
c
e
n
t
=
h
b
{\displaystyle \sec \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}={\frac {h}{b}}}
csc
θ
=
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
=
h
a
{\displaystyle \csc \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}={\frac {h}{a}}}
Ratio identities [ edit ] In the case of angles smaller than a right angle, the following identities are direct consequences of above definitions through the division identity
a
b
=
(
a
h
)
(
b
h
)
.
{\displaystyle {\frac {a}{b}}={\frac {\left({\frac {a}{h}}\right)}{\left({\frac {b}{h}}\right)}}.}
They remain valid for angles greater than 90° and for negative angles.
tan
θ
=
o
p
p
o
s
i
t
e
a
d
j
a
c
e
n
t
=
(
o
p
p
o
s
i
t
e
h
y
p
o
t
e
n
u
s
e
)
(
a
d
j
a
c
e
n
t
h
y
p
o
t
e
n
u
s
e
)
=
sin
θ
cos
θ
{\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {\left({\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}\right)}{\left({\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}\right)}}={\frac {\sin \theta }{\cos \theta }}}
cot
θ
=
a
d
j
a
c
e
n
t
o
p
p
o
s
i
t
e
=
(
a
d
j
a
c
e
n
t
a
d
j
a
c
e
n
t
)
(
o
p
p
o
s
i
t
e
a
d
j
a
c
e
n
t
)
=
1
tan
θ
=
cos
θ
sin
θ
{\displaystyle \cot \theta ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}={\frac {\left({\frac {\mathrm {adjacent} }{\mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {opposite} }{\mathrm {adjacent} }}\right)}}={\frac {1}{\tan \theta }}={\frac {\cos \theta }{\sin \theta }}}
sec
θ
=
1
cos
θ
=
h
y
p
o
t
e
n
u
s
e
a
d
j
a
c
e
n
t
{\displaystyle \sec \theta ={\frac {1}{\cos \theta }}={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}}
csc
θ
=
1
sin
θ
=
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
{\displaystyle \csc \theta ={\frac {1}{\sin \theta }}={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}}
tan
θ
=
o
p
p
o
s
i
t
e
a
d
j
a
c
e
n
t
=
(
o
p
p
o
s
i
t
e
×
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
×
a
d
j
a
c
e
n
t
)
(
a
d
j
a
c
e
n
t
×
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
×
a
d
j
a
c
e
n
t
)
=
(
h
y
p
o
t
e
n
u
s
e
a
d
j
a
c
e
n
t
)
(
h
y
p
o
t
e
n
u
s
e
o
p
p
o
s
i
t
e
)
=
sec
θ
csc
θ
{\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {\left({\frac {\mathrm {opposite} \times \mathrm {hypotenuse} }{\mathrm {opposite} \times \mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {adjacent} \times \mathrm {hypotenuse} }{\mathrm {opposite} \times \mathrm {adjacent} }}\right)}}={\frac {\left({\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}\right)}}={\frac {\sec \theta }{\csc \theta }}}
Or
tan
θ
=
sin
θ
cos
θ
=
(
1
csc
θ
)
(
1
sec
θ
)
=
(
csc
θ
sec
θ
csc
θ
)
(
csc
θ
sec
θ
sec
θ
)
=
sec
θ
csc
θ
{\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}={\frac {\left({\frac {1}{\csc \theta }}\right)}{\left({\frac {1}{\sec \theta }}\right)}}={\frac {\left({\frac {\csc \theta \sec \theta }{\csc \theta }}\right)}{\left({\frac {\csc \theta \sec \theta }{\sec \theta }}\right)}}={\frac {\sec \theta }{\csc \theta }}}
cot
θ
=
csc
θ
sec
θ
{\displaystyle \cot \theta ={\frac {\csc \theta }{\sec \theta }}}
Complementary angle identities [ edit ] Two angles whose sum is π/2 radians (90 degrees) are complementary . In the diagram, the angles at vertices A and B are complementary, so we can exchange a and b, and change θ to π/2 − θ, obtaining:
sin
(
π
/
2
−
θ
)
=
cos
θ
{\displaystyle \sin \left(\pi /2-\theta \right)=\cos \theta }
cos
(
π
/
2
−
θ
)
=
sin
θ
{\displaystyle \cos \left(\pi /2-\theta \right)=\sin \theta }
tan
(
π
/
2
−
θ
)
=
cot
θ
{\displaystyle \tan \left(\pi /2-\theta \right)=\cot \theta }
cot
(
π
/
2
−
θ
)
=
tan
θ
{\displaystyle \cot \left(\pi /2-\theta \right)=\tan \theta }
sec
(
π
/
2
−
θ
)
=
csc
θ
{\displaystyle \sec \left(\pi /2-\theta \right)=\csc \theta }
csc
(
π
/
2
−
θ
)
=
sec
θ
{\displaystyle \csc \left(\pi /2-\theta \right)=\sec \theta }
Pythagorean identities [ edit ] Identity 1:
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
The following two results follow from this and the ratio identities. To obtain the first, divide both sides of
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
cos
2
θ
{\displaystyle \cos ^{2}\theta }
sin
2
θ
{\displaystyle \sin ^{2}\theta }
tan
2
θ
+
1
=
sec
2
θ
{\displaystyle \tan ^{2}\theta +1\ =\sec ^{2}\theta }
sec
2
θ
−
tan
2
θ
=
1
{\displaystyle \sec ^{2}\theta -\tan ^{2}\theta =1}
Similarly
1
+
cot
2
θ
=
csc
2
θ
{\displaystyle 1\ +\cot ^{2}\theta =\csc ^{2}\theta }
csc
2
θ
−
cot
2
θ
=
1
{\displaystyle \csc ^{2}\theta -\cot ^{2}\theta =1}
Identity 2:
The following accounts for all three reciprocal functions.
csc
2
θ
+
sec
2
θ
−
cot
2
θ
=
2
+
tan
2
θ
{\displaystyle \csc ^{2}\theta +\sec ^{2}\theta -\cot ^{2}\theta =2\ +\tan ^{2}\theta }
Proof 2:
Refer to the triangle diagram above. Note that
a
2
+
b
2
=
h
2
{\displaystyle a^{2}+b^{2}=h^{2}}
Pythagorean theorem .
csc
2
θ
+
sec
2
θ
=
h
2
a
2
+
h
2
b
2
=
a
2
+
b
2
a
2
+
a
2
+
b
2
b
2
=
2
+
b
2
a
2
+
a
2
b
2
{\displaystyle \csc ^{2}\theta +\sec ^{2}\theta ={\frac {h^{2}}{a^{2}}}+{\frac {h^{2}}{b^{2}}}={\frac {a^{2}+b^{2}}{a^{2}}}+{\frac {a^{2}+b^{2}}{b^{2}}}=2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}}
Substituting with appropriate functions -
2
+
b
2
a
2
+
a
2
b
2
=
2
+
tan
2
θ
+
cot
2
θ
{\displaystyle 2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}=2\ +\tan ^{2}\theta +\cot ^{2}\theta }
Rearranging gives:
csc
2
θ
+
sec
2
θ
−
cot
2
θ
=
2
+
tan
2
θ
{\displaystyle \csc ^{2}\theta +\sec ^{2}\theta -\cot ^{2}\theta =2\ +\tan ^{2}\theta }
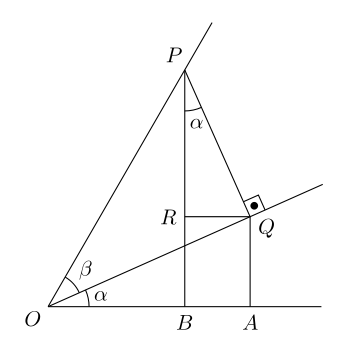
Angle sum identities [ edit ] Illustration of the sum formula. Draw a horizontal line (the x -axis); mark an origin O. Draw a line from O at an angle
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
x -axis is
α
+
β
{\displaystyle \alpha +\beta }
Place P on the line defined by
α
+
β
{\displaystyle \alpha +\beta }
Let PQ be a line perpendicular to line OQ defined by angle
α
{\displaystyle \alpha }
∴
{\displaystyle \therefore }
Let QA be a perpendicular from point A on the x -axis to Q and PB be a perpendicular from point B on the x -axis to P.
∴
{\displaystyle \therefore }
Draw R on PB so that QR is parallel to the x -axis.
Now angle
R
P
Q
=
α
{\displaystyle RPQ=\alpha }
O
Q
A
=
π
2
−
α
{\displaystyle OQA={\frac {\pi }{2}}-\alpha }
R
Q
O
=
α
,
R
Q
P
=
π
2
−
α
{\displaystyle RQO=\alpha ,RQP={\frac {\pi }{2}}-\alpha }
R
P
Q
=
α
{\displaystyle RPQ=\alpha }
R
P
Q
=
π
2
−
R
Q
P
=
π
2
−
(
π
2
−
R
Q
O
)
=
R
Q
O
=
α
{\displaystyle RPQ={\tfrac {\pi }{2}}-RQP={\tfrac {\pi }{2}}-({\tfrac {\pi }{2}}-RQO)=RQO=\alpha }
O
P
=
1
{\displaystyle OP=1}
P
Q
=
sin
β
{\displaystyle PQ=\sin \beta }
O
Q
=
cos
β
{\displaystyle OQ=\cos \beta }
A
Q
O
Q
=
sin
α
{\displaystyle {\frac {AQ}{OQ}}=\sin \alpha }
A
Q
=
sin
α
cos
β
{\displaystyle AQ=\sin \alpha \cos \beta }
P
R
P
Q
=
cos
α
{\displaystyle {\frac {PR}{PQ}}=\cos \alpha }
P
R
=
cos
α
sin
β
{\displaystyle PR=\cos \alpha \sin \beta }
sin
(
α
+
β
)
=
P
B
=
R
B
+
P
R
=
A
Q
+
P
R
=
sin
α
cos
β
+
cos
α
sin
β
{\displaystyle \sin(\alpha +\beta )=PB=RB+PR=AQ+PR=\sin \alpha \cos \beta +\cos \alpha \sin \beta }
By substituting
−
β
{\displaystyle -\beta }
β
{\displaystyle \beta }
reflection identities of even and odd functions , we also get:
sin
(
α
−
β
)
=
sin
α
cos
(
−
β
)
+
cos
α
sin
(
−
β
)
{\displaystyle \sin(\alpha -\beta )=\sin \alpha \cos(-\beta )+\cos \alpha \sin(-\beta )}
sin
(
α
−
β
)
=
sin
α
cos
β
−
cos
α
sin
β
{\displaystyle \sin(\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta }
Using the figure above,
O
P
=
1
{\displaystyle OP=1}
P
Q
=
sin
β
{\displaystyle PQ=\sin \beta }
O
Q
=
cos
β
{\displaystyle OQ=\cos \beta }
O
A
O
Q
=
cos
α
{\displaystyle {\frac {OA}{OQ}}=\cos \alpha }
O
A
=
cos
α
cos
β
{\displaystyle OA=\cos \alpha \cos \beta }
R
Q
P
Q
=
sin
α
{\displaystyle {\frac {RQ}{PQ}}=\sin \alpha }
R
Q
=
sin
α
sin
β
{\displaystyle RQ=\sin \alpha \sin \beta }
cos
(
α
+
β
)
=
O
B
=
O
A
−
B
A
=
O
A
−
R
Q
=
cos
α
cos
β
−
sin
α
sin
β
{\displaystyle \cos(\alpha +\beta )=OB=OA-BA=OA-RQ=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta }
By substituting
−
β
{\displaystyle -\beta }
β
{\displaystyle \beta }
reflection identities of even and odd functions , we also get:
cos
(
α
−
β
)
=
cos
α
cos
(
−
β
)
−
sin
α
sin
(
−
β
)
,
{\displaystyle \cos(\alpha -\beta )=\cos \alpha \cos(-\beta )-\sin \alpha \sin(-\beta ),}
cos
(
α
−
β
)
=
cos
α
cos
β
+
sin
α
sin
β
{\displaystyle \cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta }
Also, using the complementary angle formulae ,
cos
(
α
+
β
)
=
sin
(
π
/
2
−
(
α
+
β
)
)
=
sin
(
(
π
/
2
−
α
)
−
β
)
=
sin
(
π
/
2
−
α
)
cos
β
−
cos
(
π
/
2
−
α
)
sin
β
=
cos
α
cos
β
−
sin
α
sin
β
{\displaystyle {\begin{aligned}\cos(\alpha +\beta )&=\sin \left(\pi /2-(\alpha +\beta )\right)\\&=\sin \left((\pi /2-\alpha )-\beta \right)\\&=\sin \left(\pi /2-\alpha \right)\cos \beta -\cos \left(\pi /2-\alpha \right)\sin \beta \\&=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\\end{aligned}}}
Tangent and cotangent [ edit ] From the sine and cosine formulae, we get
tan
(
α
+
β
)
=
sin
(
α
+
β
)
cos
(
α
+
β
)
=
sin
α
cos
β
+
cos
α
sin
β
cos
α
cos
β
−
sin
α
sin
β
{\displaystyle \tan(\alpha +\beta )={\frac {\sin(\alpha +\beta )}{\cos(\alpha +\beta )}}={\frac {\sin \alpha \cos \beta +\cos \alpha \sin \beta }{\cos \alpha \cos \beta -\sin \alpha \sin \beta }}}
Dividing both numerator and denominator by
cos
α
cos
β
{\displaystyle \cos \alpha \cos \beta }
tan
(
α
+
β
)
=
tan
α
+
tan
β
1
−
tan
α
tan
β
{\displaystyle \tan(\alpha +\beta )={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}}
Subtracting
β
{\displaystyle \beta }
α
{\displaystyle \alpha }
tan
(
−
β
)
=
−
tan
β
{\displaystyle \tan(-\beta )=-\tan \beta }
tan
(
α
−
β
)
=
tan
α
+
tan
(
−
β
)
1
−
tan
α
tan
(
−
β
)
=
tan
α
−
tan
β
1
+
tan
α
tan
β
{\displaystyle \tan(\alpha -\beta )={\frac {\tan \alpha +\tan(-\beta )}{1-\tan \alpha \tan(-\beta )}}={\frac {\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }}}
Similarly, from the sine and cosine formulae, we get
cot
(
α
+
β
)
=
cos
(
α
+
β
)
sin
(
α
+
β
)
=
cos
α
cos
β
−
sin
α
sin
β
sin
α
cos
β
+
cos
α
sin
β
{\displaystyle \cot(\alpha +\beta )={\frac {\cos(\alpha +\beta )}{\sin(\alpha +\beta )}}={\frac {\cos \alpha \cos \beta -\sin \alpha \sin \beta }{\sin \alpha \cos \beta +\cos \alpha \sin \beta }}}
Then by dividing both numerator and denominator by
sin
α
sin
β
{\displaystyle \sin \alpha \sin \beta }
cot
(
α
+
β
)
=
cot
α
cot
β
−
1
cot
α
+
cot
β
{\displaystyle \cot(\alpha +\beta )={\frac {\cot \alpha \cot \beta -1}{\cot \alpha +\cot \beta }}}
Or, using
cot
θ
=
1
tan
θ
{\displaystyle \cot \theta ={\frac {1}{\tan \theta }}}
cot
(
α
+
β
)
=
1
−
tan
α
tan
β
tan
α
+
tan
β
=
1
tan
α
tan
β
−
1
1
tan
α
+
1
tan
β
=
cot
α
cot
β
−
1
cot
α
+
cot
β
{\displaystyle \cot(\alpha +\beta )={\frac {1-\tan \alpha \tan \beta }{\tan \alpha +\tan \beta }}={\frac {{\frac {1}{\tan \alpha \tan \beta }}-1}{{\frac {1}{\tan \alpha }}+{\frac {1}{\tan \beta }}}}={\frac {\cot \alpha \cot \beta -1}{\cot \alpha +\cot \beta }}}
Using
cot
(
−
β
)
=
−
cot
β
{\displaystyle \cot(-\beta )=-\cot \beta }
cot
(
α
−
β
)
=
cot
α
cot
(
−
β
)
−
1
cot
α
+
cot
(
−
β
)
=
cot
α
cot
β
+
1
cot
β
−
cot
α
{\displaystyle \cot(\alpha -\beta )={\frac {\cot \alpha \cot(-\beta )-1}{\cot \alpha +\cot(-\beta )}}={\frac {\cot \alpha \cot \beta +1}{\cot \beta -\cot \alpha }}}
Double-angle identities [ edit ] From the angle sum identities, we get
sin
(
2
θ
)
=
2
sin
θ
cos
θ
{\displaystyle \sin(2\theta )=2\sin \theta \cos \theta }
and
cos
(
2
θ
)
=
cos
2
θ
−
sin
2
θ
{\displaystyle \cos(2\theta )=\cos ^{2}\theta -\sin ^{2}\theta }
The Pythagorean identities give the two alternative forms for the latter of these:
cos
(
2
θ
)
=
2
cos
2
θ
−
1
{\displaystyle \cos(2\theta )=2\cos ^{2}\theta -1}
cos
(
2
θ
)
=
1
−
2
sin
2
θ
{\displaystyle \cos(2\theta )=1-2\sin ^{2}\theta }
The angle sum identities also give
tan
(
2
θ
)
=
2
tan
θ
1
−
tan
2
θ
=
2
cot
θ
−
tan
θ
{\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}={\frac {2}{\cot \theta -\tan \theta }}}
cot
(
2
θ
)
=
cot
2
θ
−
1
2
cot
θ
=
cot
θ
−
tan
θ
2
{\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}={\frac {\cot \theta -\tan \theta }{2}}}
It can also be proved using Euler's formula
e
i
φ
=
cos
φ
+
i
sin
φ
{\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi }
Squaring both sides yields
e
i
2
φ
=
(
cos
φ
+
i
sin
φ
)
2
{\displaystyle e^{i2\varphi }=(\cos \varphi +i\sin \varphi )^{2}}
But replacing the angle with its doubled version, which achieves the same result in the left side of the equation, yields
e
i
2
φ
=
cos
2
φ
+
i
sin
2
φ
{\displaystyle e^{i2\varphi }=\cos 2\varphi +i\sin 2\varphi }
It follows that
(
cos
φ
+
i
sin
φ
)
2
=
cos
2
φ
+
i
sin
2
φ
{\displaystyle (\cos \varphi +i\sin \varphi )^{2}=\cos 2\varphi +i\sin 2\varphi }
Expanding the square and simplifying on the left hand side of the equation gives
i
(
2
sin
φ
cos
φ
)
+
cos
2
φ
−
sin
2
φ
=
cos
2
φ
+
i
sin
2
φ
{\displaystyle i(2\sin \varphi \cos \varphi )+\cos ^{2}\varphi -\sin ^{2}\varphi \ =\cos 2\varphi +i\sin 2\varphi }
Because the imaginary and real parts have to be the same, we are left with the original identities
cos
2
φ
−
sin
2
φ
=
cos
2
φ
{\displaystyle \cos ^{2}\varphi -\sin ^{2}\varphi \ =\cos 2\varphi }
and also
2
sin
φ
cos
φ
=
sin
2
φ
{\displaystyle 2\sin \varphi \cos \varphi =\sin 2\varphi }
Half-angle identities [ edit ] The two identities giving the alternative forms for cos 2θ lead to the following equations:
cos
θ
2
=
±
1
+
cos
θ
2
,
{\displaystyle \cos {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{2}}},}
sin
θ
2
=
±
1
−
cos
θ
2
.
{\displaystyle \sin {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{2}}}.}
The sign of the square root needs to be chosen properly—note that if 2π is added to θ, the quantities inside the square roots are unchanged, but the left-hand-sides of the equations change sign. Therefore, the correct sign to use depends on the value of θ.
For the tan function, the equation is:
tan
θ
2
=
±
1
−
cos
θ
1
+
cos
θ
.
{\displaystyle \tan {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}.}
Then multiplying the numerator and denominator inside the square root by (1 + cos θ) and using Pythagorean identities leads to:
tan
θ
2
=
sin
θ
1
+
cos
θ
.
{\displaystyle \tan {\frac {\theta }{2}}={\frac {\sin \theta }{1+\cos \theta }}.}
Also, if the numerator and denominator are both multiplied by (1 - cos θ), the result is:
tan
θ
2
=
1
−
cos
θ
sin
θ
.
{\displaystyle \tan {\frac {\theta }{2}}={\frac {1-\cos \theta }{\sin \theta }}.}
This also gives:
tan
θ
2
=
csc
θ
−
cot
θ
.
{\displaystyle \tan {\frac {\theta }{2}}=\csc \theta -\cot \theta .}
Similar manipulations for the cot function give:
cot
θ
2
=
±
1
+
cos
θ
1
−
cos
θ
=
1
+
cos
θ
sin
θ
=
sin
θ
1
−
cos
θ
=
csc
θ
+
cot
θ
.
{\displaystyle \cot {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta .}
Miscellaneous – the triple tangent identity [ edit ] If
ψ
+
θ
+
ϕ
=
π
=
{\displaystyle \psi +\theta +\phi =\pi =}
ψ
{\displaystyle \psi }
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
tan
(
ψ
)
+
tan
(
θ
)
+
tan
(
ϕ
)
=
tan
(
ψ
)
tan
(
θ
)
tan
(
ϕ
)
.
{\displaystyle \tan(\psi )+\tan(\theta )+\tan(\phi )=\tan(\psi )\tan(\theta )\tan(\phi ).}
Proof:[1]
ψ
=
π
−
θ
−
ϕ
tan
(
ψ
)
=
tan
(
π
−
θ
−
ϕ
)
=
−
tan
(
θ
+
ϕ
)
=
−
tan
θ
−
tan
ϕ
1
−
tan
θ
tan
ϕ
=
tan
θ
+
tan
ϕ
tan
θ
tan
ϕ
−
1
(
tan
θ
tan
ϕ
−
1
)
tan
ψ
=
tan
θ
+
tan
ϕ
tan
ψ
tan
θ
tan
ϕ
−
tan
ψ
=
tan
θ
+
tan
ϕ
tan
ψ
tan
θ
tan
ϕ
=
tan
ψ
+
tan
θ
+
tan
ϕ
{\displaystyle {\begin{aligned}\psi &=\pi -\theta -\phi \\\tan(\psi )&=\tan(\pi -\theta -\phi )\\&=-\tan(\theta +\phi )\\&={\frac {-\tan \theta -\tan \phi }{1-\tan \theta \tan \phi }}\\&={\frac {\tan \theta +\tan \phi }{\tan \theta \tan \phi -1}}\\(\tan \theta \tan \phi -1)\tan \psi &=\tan \theta +\tan \phi \\\tan \psi \tan \theta \tan \phi -\tan \psi &=\tan \theta +\tan \phi \\\tan \psi \tan \theta \tan \phi &=\tan \psi +\tan \theta +\tan \phi \\\end{aligned}}}
Miscellaneous – the triple cotangent identity [ edit ] If
ψ
+
θ
+
ϕ
=
π
2
=
{\displaystyle \psi +\theta +\phi ={\tfrac {\pi }{2}}=}
cot
(
ψ
)
+
cot
(
θ
)
+
cot
(
ϕ
)
=
cot
(
ψ
)
cot
(
θ
)
cot
(
ϕ
)
{\displaystyle \cot(\psi )+\cot(\theta )+\cot(\phi )=\cot(\psi )\cot(\theta )\cot(\phi )}
Proof:
Replace each of
ψ
{\displaystyle \psi }
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
Given
ψ
+
θ
+
ϕ
=
π
2
{\displaystyle \psi +\theta +\phi ={\tfrac {\pi }{2}}}
∴
(
π
2
−
ψ
)
+
(
π
2
−
θ
)
+
(
π
2
−
ϕ
)
=
3
π
2
−
(
ψ
+
θ
+
ϕ
)
=
3
π
2
−
π
2
=
π
{\displaystyle \therefore ({\tfrac {\pi }{2}}-\psi )+({\tfrac {\pi }{2}}-\theta )+({\tfrac {\pi }{2}}-\phi )={\tfrac {3\pi }{2}}-(\psi +\theta +\phi )={\tfrac {3\pi }{2}}-{\tfrac {\pi }{2}}=\pi }
so the result follows from the triple tangent identity.
Sum to product identities [ edit ]
sin
θ
±
sin
ϕ
=
2
sin
(
θ
±
ϕ
2
)
cos
(
θ
∓
ϕ
2
)
{\displaystyle \sin \theta \pm \sin \phi =2\sin \left({\frac {\theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)}
cos
θ
+
cos
ϕ
=
2
cos
(
θ
+
ϕ
2
)
cos
(
θ
−
ϕ
2
)
{\displaystyle \cos \theta +\cos \phi =2\cos \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)}
cos
θ
−
cos
ϕ
=
−
2
sin
(
θ
+
ϕ
2
)
sin
(
θ
−
ϕ
2
)
{\displaystyle \cos \theta -\cos \phi =-2\sin \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)}
Proof of sine identities [ edit ] First, start with the sum-angle identities:
sin
(
α
+
β
)
=
sin
α
cos
β
+
cos
α
sin
β
{\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta }
sin
(
α
−
β
)
=
sin
α
cos
β
−
cos
α
sin
β
{\displaystyle \sin(\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta }
By adding these together,
sin
(
α
+
β
)
+
sin
(
α
−
β
)
=
sin
α
cos
β
+
cos
α
sin
β
+
sin
α
cos
β
−
cos
α
sin
β
=
2
sin
α
cos
β
{\displaystyle \sin(\alpha +\beta )+\sin(\alpha -\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta +\sin \alpha \cos \beta -\cos \alpha \sin \beta =2\sin \alpha \cos \beta }
Similarly, by subtracting the two sum-angle identities,
sin
(
α
+
β
)
−
sin
(
α
−
β
)
=
sin
α
cos
β
+
cos
α
sin
β
−
sin
α
cos
β
+
cos
α
sin
β
=
2
cos
α
sin
β
{\displaystyle \sin(\alpha +\beta )-\sin(\alpha -\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta -\sin \alpha \cos \beta +\cos \alpha \sin \beta =2\cos \alpha \sin \beta }
Let
α
+
β
=
θ
{\displaystyle \alpha +\beta =\theta }
α
−
β
=
ϕ
{\displaystyle \alpha -\beta =\phi }
∴
α
=
θ
+
ϕ
2
{\displaystyle \therefore \alpha ={\frac {\theta +\phi }{2}}}
β
=
θ
−
ϕ
2
{\displaystyle \beta ={\frac {\theta -\phi }{2}}}
Substitute
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
sin
θ
+
sin
ϕ
=
2
sin
(
θ
+
ϕ
2
)
cos
(
θ
−
ϕ
2
)
{\displaystyle \sin \theta +\sin \phi =2\sin \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)}
sin
θ
−
sin
ϕ
=
2
cos
(
θ
+
ϕ
2
)
sin
(
θ
−
ϕ
2
)
=
2
sin
(
θ
−
ϕ
2
)
cos
(
θ
+
ϕ
2
)
{\displaystyle \sin \theta -\sin \phi =2\cos \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)=2\sin \left({\frac {\theta -\phi }{2}}\right)\cos \left({\frac {\theta +\phi }{2}}\right)}
Therefore,
sin
θ
±
sin
ϕ
=
2
sin
(
θ
±
ϕ
2
)
cos
(
θ
∓
ϕ
2
)
{\displaystyle \sin \theta \pm \sin \phi =2\sin \left({\frac {\theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)}
Proof of cosine identities [ edit ] Similarly for cosine, start with the sum-angle identities:
cos
(
α
+
β
)
=
cos
α
cos
β
−
sin
α
sin
β
{\displaystyle \cos(\alpha +\beta )=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta }
cos
(
α
−
β
)
=
cos
α
cos
β
+
sin
α
sin
β
{\displaystyle \cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta }
Again, by adding and subtracting
cos
(
α
+
β
)
+
cos
(
α
−
β
)
=
cos
α
cos
β
−
sin
α
sin
β
+
cos
α
cos
β
+
sin
α
sin
β
=
2
cos
α
cos
β
{\displaystyle \cos(\alpha +\beta )+\cos(\alpha -\beta )=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta +\cos \alpha \cos \beta +\sin \alpha \sin \beta =2\cos \alpha \cos \beta }
cos
(
α
+
β
)
−
cos
(
α
−
β
)
=
cos
α
cos
β
−
sin
α
sin
β
−
cos
α
cos
β
−
sin
α
sin
β
=
−
2
sin
α
sin
β
{\displaystyle \cos(\alpha +\beta )-\cos(\alpha -\beta )=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta -\cos \alpha \cos \beta -\sin \alpha \sin \beta =-2\sin \alpha \sin \beta }
Substitute
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
cos
θ
+
cos
ϕ
=
2
cos
(
θ
+
ϕ
2
)
cos
(
θ
−
ϕ
2
)
{\displaystyle \cos \theta +\cos \phi =2\cos \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)}
cos
θ
−
cos
ϕ
=
−
2
sin
(
θ
+
ϕ
2
)
sin
(
θ
−
ϕ
2
)
{\displaystyle \cos \theta -\cos \phi =-2\sin \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)}
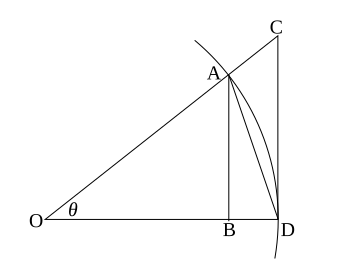
Inequalities [ edit ] Illustration of the sine and tangent inequalities. The figure at the right shows a sector of a circle with radius 1. The sector is θ /(2π )θ /2θ < π /2
O
A
=
O
D
=
1
{\displaystyle OA=OD=1}
A
B
=
sin
θ
{\displaystyle AB=\sin \theta }
C
D
=
tan
θ
{\displaystyle CD=\tan \theta }
The area of triangle OAD AB /2sin(θ )/2 . The area of triangle OCD CD /2tan(θ )/2 .
Since triangle OAD OCD
sin
θ
<
θ
<
tan
θ
.
{\displaystyle \sin \theta <\theta <\tan \theta .}
This geometric argument relies on definitions of arc length and
area , which act as assumptions, so it is rather a condition imposed in construction of trigonometric functions than
a provable property.[2] θ > π /2θ > 1sin θ ≤ 1 (because of the Pythagorean identity), so sin θ < θ . So we have
sin
θ
θ
<
1
i
f
0
<
θ
.
{\displaystyle {\frac {\sin \theta }{\theta }}<1\ \ \ \mathrm {if} \ \ \ 0<\theta .}
For negative values of θ
sin
θ
θ
=
sin
(
−
θ
)
−
θ
<
1.
{\displaystyle {\frac {\sin \theta }{\theta }}={\frac {\sin(-\theta )}{-\theta }}<1.}
Hence
sin
θ
θ
<
1
if
θ
≠
0
,
{\displaystyle {\frac {\sin \theta }{\theta }}<1\quad {\text{if }}\quad \theta \neq 0,}
and
tan
θ
θ
>
1
if
0
<
θ
<
π
2
.
{\displaystyle {\frac {\tan \theta }{\theta }}>1\quad {\text{if }}\quad 0<\theta <{\frac {\pi }{2}}.}
Identities involving calculus [ edit ] Preliminaries [ edit ]
lim
θ
→
0
sin
θ
=
0
{\displaystyle \lim _{\theta \to 0}{\sin \theta }=0}
lim
θ
→
0
cos
θ
=
1
{\displaystyle \lim _{\theta \to 0}{\cos \theta }=1}
Sine and angle ratio identity [ edit ]
lim
θ
→
0
sin
θ
θ
=
1
{\displaystyle \lim _{\theta \to 0}{\frac {\sin \theta }{\theta }}=1}
In other words, the function sine is differentiable at 0, and its derivative is 1.
Proof: From the previous inequalities, we have, for small angles
sin
θ
<
θ
<
tan
θ
{\displaystyle \sin \theta <\theta <\tan \theta }
Therefore,
sin
θ
θ
<
1
<
tan
θ
θ
{\displaystyle {\frac {\sin \theta }{\theta }}<1<{\frac {\tan \theta }{\theta }}}
Consider the right-hand inequality. Since
tan
θ
=
sin
θ
cos
θ
{\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}}
∴
1
<
sin
θ
θ
cos
θ
{\displaystyle \therefore 1<{\frac {\sin \theta }{\theta \cos \theta }}}
Multiply through by
cos
θ
{\displaystyle \cos \theta }
cos
θ
<
sin
θ
θ
{\displaystyle \cos \theta <{\frac {\sin \theta }{\theta }}}
Combining with the left-hand inequality:
cos
θ
<
sin
θ
θ
<
1
{\displaystyle \cos \theta <{\frac {\sin \theta }{\theta }}<1}
Taking
cos
θ
{\displaystyle \cos \theta }
θ
→
0
{\displaystyle \theta \to 0}
lim
θ
→
0
cos
θ
=
1
{\displaystyle \lim _{\theta \to 0}{\cos \theta }=1}
Therefore,
lim
θ
→
0
sin
θ
θ
=
1
{\displaystyle \lim _{\theta \to 0}{\frac {\sin \theta }{\theta }}=1}
Cosine and angle ratio identity [ edit ]
lim
θ
→
0
1
−
cos
θ
θ
=
0
{\displaystyle \lim _{\theta \to 0}{\frac {1-\cos \theta }{\theta }}=0}
Proof:
1
−
cos
θ
θ
=
1
−
cos
2
θ
θ
(
1
+
cos
θ
)
=
sin
2
θ
θ
(
1
+
cos
θ
)
=
(
sin
θ
θ
)
×
sin
θ
×
(
1
1
+
cos
θ
)
{\displaystyle {\begin{aligned}{\frac {1-\cos \theta }{\theta }}&={\frac {1-\cos ^{2}\theta }{\theta (1+\cos \theta )}}\\&={\frac {\sin ^{2}\theta }{\theta (1+\cos \theta )}}\\&=\left({\frac {\sin \theta }{\theta }}\right)\times \sin \theta \times \left({\frac {1}{1+\cos \theta }}\right)\\\end{aligned}}}
The limits of those three quantities are 1, 0, and 1/2, so the resultant limit is zero.
Cosine and square of angle ratio identity [ edit ]
lim
θ
→
0
1
−
cos
θ
θ
2
=
1
2
{\displaystyle \lim _{\theta \to 0}{\frac {1-\cos \theta }{\theta ^{2}}}={\frac {1}{2}}}
Proof:
As in the preceding proof,
1
−
cos
θ
θ
2
=
sin
θ
θ
×
sin
θ
θ
×
1
1
+
cos
θ
.
{\displaystyle {\frac {1-\cos \theta }{\theta ^{2}}}={\frac {\sin \theta }{\theta }}\times {\frac {\sin \theta }{\theta }}\times {\frac {1}{1+\cos \theta }}.}
The limits of those three quantities are 1, 1, and 1/2, so the resultant limit is 1/2.
Proof of compositions of trig and inverse trig functions [ edit ] All these functions follow from the Pythagorean trigonometric identity. We can prove for instance the function
sin
[
arctan
(
x
)
]
=
x
1
+
x
2
{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}}
Proof:
We start from
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
Then we divide this equation (I) by
cos
2
θ
{\displaystyle \cos ^{2}\theta }
cos
2
θ
=
1
tan
2
θ
+
1
{\displaystyle \cos ^{2}\theta ={\frac {1}{\tan ^{2}\theta +1}}}
1
−
sin
2
θ
=
1
tan
2
θ
+
1
{\displaystyle 1-\sin ^{2}\theta ={\frac {1}{\tan ^{2}\theta +1}}}
Then use the substitution
θ
=
arctan
(
x
)
{\displaystyle \theta =\arctan(x)}
1
−
sin
2
[
arctan
(
x
)
]
=
1
tan
2
[
arctan
(
x
)
]
+
1
{\displaystyle 1-\sin ^{2}[\arctan(x)]={\frac {1}{\tan ^{2}[\arctan(x)]+1}}}
sin
2
[
arctan
(
x
)
]
=
tan
2
[
arctan
(
x
)
]
tan
2
[
arctan
(
x
)
]
+
1
{\displaystyle \sin ^{2}[\arctan(x)]={\frac {\tan ^{2}[\arctan(x)]}{\tan ^{2}[\arctan(x)]+1}}}
Then we use the identity
tan
[
arctan
(
x
)
]
≡
x
{\displaystyle \tan[\arctan(x)]\equiv x}
sin
[
arctan
(
x
)
]
=
x
x
2
+
1
{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {x^{2}+1}}}}
And initial Pythagorean trigonometric identity proofed...
sin
2
θ
{\displaystyle \sin ^{2}\theta }
sin
2
θ
=
1
1
1
+
1
tan
2
θ
{\displaystyle \sin ^{2}\theta ={\frac {\frac {1}{1}}{1+{\frac {1}{\tan ^{2}\theta }}}}}
sin
2
θ
=
tan
2
θ
tan
2
θ
+
1
{\displaystyle \sin ^{2}\theta ={\frac {\tan ^{2}\theta }{\tan ^{2}\theta +1}}}
Then use the substitution
θ
=
arctan
(
x
)
{\displaystyle \theta =\arctan(x)}
sin
2
[
arctan
(
x
)
]
=
tan
2
[
arctan
(
x
)
]
tan
2
[
arctan
(
x
)
]
+
1
{\displaystyle \sin ^{2}[\arctan(x)]={\frac {\tan ^{2}[\arctan(x)]}{\tan ^{2}[\arctan(x)]+1}}}
Then we use the identity
tan
[
arctan
(
x
)
]
≡
x
{\displaystyle \tan[\arctan(x)]\equiv x}
sin
[
arctan
(
x
)
]
=
x
x
2
+
1
{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {x^{2}+1}}}}
And initial Pythagorean trigonometric identity proofed...
[
arctan
(
x
)
]
=
[
arcsin
(
x
x
2
+
1
)
]
{\displaystyle [\arctan(x)]=[\arcsin({\frac {x}{\sqrt {x^{2}+1}}})]}
y
=
x
x
2
+
1
{\displaystyle y={\frac {x}{\sqrt {x^{2}+1}}}}
y
2
=
x
2
x
2
+
1
{\displaystyle y^{2}={\frac {x^{2}}{x^{2}+1}}}
x
=
y
1
−
y
2
{\displaystyle x={\frac {y}{\sqrt {1-y^{2}}}}}
x
2
=
y
2
1
−
y
2
{\displaystyle x^{2}={\frac {y^{2}}{1-y^{2}}}}
y
2
=
y
2
(
1
−
y
2
)
y
2
(
1
−
y
2
)
+
1
{\displaystyle y^{2}={\frac {\frac {y^{2}}{(1-y^{2})}}{{\frac {y^{2}}{(1-y^{2})}}+1}}}
y
2
=
y
2
(
1
−
y
2
)
1
(
1
−
y
2
)
{\displaystyle y^{2}={\frac {\frac {y^{2}}{(1-y^{2})}}{\frac {1}{(1-y^{2})}}}}
So it's true:
y
2
=
y
2
{\displaystyle y^{2}=y^{2}}
x
=
y
1
−
y
2
{\displaystyle x={\frac {y}{\sqrt {1-y^{2}}}}}
[
arctan
(
x
)
]
=
[
arcsin
(
x
x
2
+
1
)
]
=
[
arcsin
(
y
)
]
=
[
arctan
(
y
1
−
y
2
)
]
{\displaystyle [\arctan(x)]=[\arcsin({\frac {x}{\sqrt {x^{2}+1}}})]=[\arcsin(y)]=[\arctan({\frac {y}{\sqrt {1-y^{2}}}})]}
[
arcsin
(
x
)
]
=
[
arctan
(
x
1
−
x
2
)
]
{\displaystyle [\arcsin(x)]=[\arctan({\frac {x}{\sqrt {1-x^{2}}}})]}
[
arccos
(
x
)
]
{\displaystyle [\arccos(x)]}
cos
[
arccos
(
x
)
]
=
x
{\displaystyle \cos[\arccos(x)]=x}
cos
(
π
2
−
(
π
2
−
[
arccos
(
x
)
]
)
)
=
x
{\displaystyle \cos({\frac {\pi }{2}}-({\frac {\pi }{2}}-[\arccos(x)]))=x}
sin
(
π
2
−
[
arccos
(
x
)
]
)
=
x
{\displaystyle \sin({\frac {\pi }{2}}-[\arccos(x)])=x}
π
2
−
[
arccos
(
x
)
]
=
[
arcsin
(
x
)
]
{\displaystyle {\frac {\pi }{2}}-[\arccos(x)]=[\arcsin(x)]}
[
arccos
(
x
)
]
=
π
2
−
[
arcsin
(
x
)
]
{\displaystyle [\arccos(x)]={\frac {\pi }{2}}-[\arcsin(x)]}
[
arcsin
(
x
)
]
{\displaystyle [\arcsin(x)]}
[
arccos
(
x
)
]
=
π
2
−
[
arctan
(
x
1
−
x
2
)
]
{\displaystyle [\arccos(x)]={\frac {\pi }{2}}-[\arctan({\frac {x}{\sqrt {1-x^{2}}}})]}
[
arccos
(
x
)
]
=
π
2
−
[
arccot
(
1
−
x
2
x
)
]
{\displaystyle [\arccos(x)]={\frac {\pi }{2}}-[\operatorname {arccot}({\frac {\sqrt {1-x^{2}}}{x}})]}
And finally we have [arccos] expressed through [arctan]...
[
arccos
(
x
)
]
=
[
arctan
(
1
−
x
2
x
)
]
{\displaystyle [\arccos(x)]=[\arctan({\frac {\sqrt {1-x^{2}}}{x}})]}
See also [ edit ] References [ edit ] 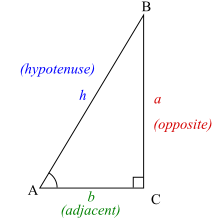












































































































































![{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d3ed8cedb4c73b01b65314a15152647c9000086)



![{\displaystyle 1-\sin ^{2}[\arctan(x)]={\frac {1}{\tan ^{2}[\arctan(x)]+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0bb45d076e27715801c0437e364d4b1f45dfb1a)
![{\displaystyle \sin ^{2}[\arctan(x)]={\frac {\tan ^{2}[\arctan(x)]}{\tan ^{2}[\arctan(x)]+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31457873262613ebf792de2499d564919e4d18c9)
![{\displaystyle \tan[\arctan(x)]\equiv x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49ce3dc146ff12eb2efb89a4388afcb984b7da8e)
![{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {x^{2}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c5222bb21dc2d342d1363c855694bae8b967914)


![{\displaystyle [\arctan(x)]=[\arcsin({\frac {x}{\sqrt {x^{2}+1}}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbc17437ca395ab8ec9e04f2d21096288df5b9a2)







![{\displaystyle [\arctan(x)]=[\arcsin({\frac {x}{\sqrt {x^{2}+1}}})]=[\arcsin(y)]=[\arctan({\frac {y}{\sqrt {1-y^{2}}}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbaafc98c5960a737537039cff02fdd72be65da)
![{\displaystyle [\arcsin(x)]=[\arctan({\frac {x}{\sqrt {1-x^{2}}}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/552a4ab628e13245dc277ab57029427f50ee8ebd)
![{\displaystyle [\arccos(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f61004b1d4ad7ff39f9a7ee50976ec672d2c198)
![{\displaystyle \cos[\arccos(x)]=x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9d5691af1ed2de3248e08dbaf90a24a80c1c816)
![{\displaystyle \cos({\frac {\pi }{2}}-({\frac {\pi }{2}}-[\arccos(x)]))=x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7562bfeec9737b56e7affe3409239315302693c3)
![{\displaystyle \sin({\frac {\pi }{2}}-[\arccos(x)])=x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ad20b817a17336b1fc1af8c339a3d7e4cf111f6)
![{\displaystyle {\frac {\pi }{2}}-[\arccos(x)]=[\arcsin(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20f54833eb7dbe561e4cb31e51453ebd14a5cc51)
![{\displaystyle [\arccos(x)]={\frac {\pi }{2}}-[\arcsin(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfc6a970c74fe335d2b0684f23027e6ca255a9cc)
![{\displaystyle [\arcsin(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef6f2837ad8f82968478d6c5e93863549f833207)
![{\displaystyle [\arccos(x)]={\frac {\pi }{2}}-[\arctan({\frac {x}{\sqrt {1-x^{2}}}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6675d621ebaf7c4c4b10adbee9a1fd4b6f1d6eb)
![{\displaystyle [\arccos(x)]={\frac {\pi }{2}}-[\operatorname {arccot}({\frac {\sqrt {1-x^{2}}}{x}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4fe5f411d564cd54abb12c188ca5885150f1949)
![{\displaystyle [\arccos(x)]=[\arctan({\frac {\sqrt {1-x^{2}}}{x}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13428b7bd426702f18227deb2d8da5f116c16db4)