Punnett square


The Punnett square is a square diagram that is used to predict the genotypes of a particular cross or breeding experiment. It is named after Reginald C. Punnett, who devised the approach in 1905.[3][4][5][6][7][8] The diagram is used by biologists to determine the probability of an offspring having a particular genotype. The Punnett square is a tabular summary of possible combinations of maternal alleles with paternal alleles.[9] These tables can be used to examine the genotypical outcome probabilities of the offspring of a single trait (allele), or when crossing multiple traits from the parents. The Punnett square is a visual representation of Mendelian inheritance, a fundamental concept in genetics which is discovery of Gregor Mendel.[10] For multiple traits, using the "forked-line method" is typically much easier than the Punnett square. Phenotypes may be predicted with at least better-than-chance accuracy using a Punnett square, but the phenotype that may appear in the presence of a given genotype can in some instances be influenced by many other factors, as when polygenic inheritance and/or epigenetics are at work.
Zygosity[edit]
Zygosity refers to the grade of similarity between the alleles that determine one specific trait in an organism. In its simplest form, a pair of alleles can be either homozygous or heterozygous. Homozygosity, with homo relating to same while zygous pertains to a zygote, is seen when a combination of either two dominant or two recessive alleles code for the same trait. Recessive are always lowercase letters. For example, using 'A' as the representative character for each allele, a homozygous dominant pair's genotype would be depicted as 'AA', while homozygous recessive is shown as 'aa'. Heterozygosity, with hetero associated with different, can only be 'Aa' (the capital letter is always presented first by convention). The phenotype of a homozygous dominant pair is 'A', or dominant, while the opposite is true for homozygous recessive. Heterozygous pairs always have a dominant phenotype.[11] To a lesser degree, hemizygosity[12] and nullizygosity[13] can also be seen in gene pairs.
Monohybrid cross[edit]
"Mono-" means "one"; this cross indicates that the examination of a single trait. This could mean (for example) eye color. Each genetic locus is always represented by two letters. So in the case of eye color, say "B = Brown eyes" and "b = green eyes". In this example, both parents have the genotype Bb. For the example of eye color, this would mean they both have brown eyes. They can produce gametes that contain either the B or the b allele. (It is conventional in genetics to use capital letters to indicate dominant alleles and lower-case letters to indicate recessive alleles.) The probability of an individual offspring's having the genotype BB is 25%, Bb is 50%, and bb is 25%. The ratio of the phenotypes is 3:1, typical for a monohybrid cross. When assessing phenotype from this, "3" of the offspring have "Brown" eyes and only one offspring has "green" eyes. (3 are "B?" and 1 is "bb")
Paternal Maternal |
B | b |
|---|---|---|
| B | Xb | Y |
| b | XB | Xb |
The way in which the B and b alleles interact with each other to affect the appearance of the offspring depends on how the gene products (proteins) interact (see Mendelian inheritance). This can include lethal effects and epistasis (where one allele masks another, regardless of dominant or recessive status).
Dihybrid cross[edit]
More complicated crosses can be made by looking at two or more genes. The Punnett square works, however, only if the genes are independent of each other, which means that having a particular allele of gene "A" does not alter the probability of possessing an allele of gene "B". This is equivalent to stating that the genes are not linked, so that the two genes do not tend to sort together during meiosis.
The following example illustrates a dihybrid cross between two double-heterozygote pea plants. R represents the dominant allele for shape (round), while r represents the recessive allele (wrinkled). A represents the dominant allele for color (yellow), while a represents the recessive allele (green). If each plant has the genotype RrAa, and since the alleles for shape and color genes are independent, then they can produce four types of gametes with all possible combinations: RA, Ra, rA, and ra.
| RA | Ra | rA | ra | |
|---|---|---|---|---|
| RA | RRAA | RRAa | RrAA | RrAa |
| Ra | RRAa | RRaa | RrAa | Rraa |
| rA | RrAA | RrAa | rrAA | rrAa |
| ra | RrAa | Rraa | rrAa | rraa |
Since dominant traits mask recessive traits (assuming no epistasis), there are nine combinations that have the phenotype round yellow, three that are round green, three that are wrinkled yellow, and one that is wrinkled green. The ratio 9:3:3:1 is the expected outcome when crossing two double-heterozygous parents with unlinked genes. Any other ratio indicates that something else has occurred (such as lethal alleles, epistasis, linked genes, etc.).
Forked-line method[edit]
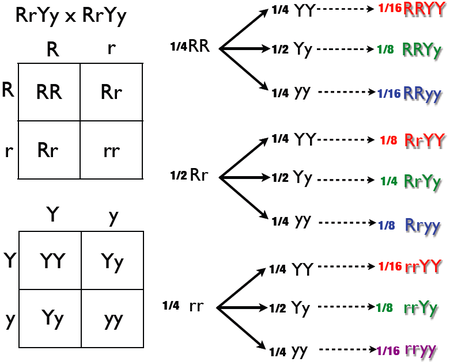
The forked-line method (also known as the tree method and the branching system) can also solve dihybrid and multi-hybrid crosses. A problem is converted to a series of monohybrid crosses, and the results are combined in a tree. However, a tree produces the same result as a Punnett square in less time and with more clarity. The example below assesses another double-heterozygote cross using RrYy x RrYy. As stated above, the phenotypic ratio is expected to be 9:3:3:1 if crossing unlinked genes from two double-heterozygotes. The genotypic ratio was obtained in the diagram below, this diagram will have more branches than if only analyzing for phenotypic ratio.


See also[edit]
- Mendelian inheritance
- Karnaugh map, a similar diagram used for Boolean algebra simplification
References[edit]
- ^ Mendel, Gregor Johann (1866) [1865]. Versuche über Pflanzen-Hybriden. Verhandlungen des naturforschenden Vereins (in German and English). Vol. IV (Separate ed.). Brno: Verlag des naturforschender Vereins zu Brünn / Georg Gastl's Buchdruckerei /. p. 14. Archived from the original on 2021-03-29. Retrieved 2020-06-01.
{{cite book}}:|work=ignored (help) - ^ Mendel, Gregor Johann (1866) [1865]. Versuche über Pflanzen-Hybriden. Verhandlungen des naturforschenden Vereins (in German and English). Vol. IV (Separate ed.). Brno: Verlag des naturforschender Vereins zu Brünn / Georg Gastl's Buchdruckerei. p. 47. Archived from the original on 2021-03-29. Retrieved 2020-06-01.
{{cite book}}:|work=ignored (help) - ^ Punnett, Reginald Crundall (1907). Mendelism (2 ed.). London, UK: Macmillan. (NB. The 1905 first edition of this book does not contain the Punnett square. In 1911, the third edition gives a more thorough explanation.)
- ^ Edwards, Anthony William Fairbank (March 2012). "Punnett's square". Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences. 43 (1): 219–224. doi:10.1016/j.shpsc.2011.11.011. PMID 22326091. Abstract:
The origin and development of Punnett's Square for the enumeration and display of genotypes arising in a cross in Mendelian genetics is described. Due to R. C. Punnett, the idea evolved through the work of the 'Cambridge geneticists', including Punnett's colleagues William Bateson, E. R. Saunders and R. H. Lock, soon after the rediscovery of Mendel's paper in 1900. These geneticists were thoroughly familiar with Mendel's paper, which itself contained a similar square diagram. A previously-unpublished three-factor diagram by Sir Francis Galton existing in the Bateson correspondence in Cambridge University Library is then described. Finally the connection between Punnett's Square and Venn Diagrams is emphasized, and it is pointed out that Punnett, Lock and John Venn overlapped as Fellows of Gonville and Caius College, Cambridge.
- ^ Edwards, Anthony William Fairbank (September 2012). "Reginald Crundall Punnett: First Arthur Balfour Professor of Genetics, Cambridge, 1912". Perspectives. Genetics. 192 (1). Gonville and Caius College, Cambridge, UK: Genetics Society of America: 3–13. doi:10.1534/genetics.112.143552. PMC 3430543. PMID 22964834. pp. 5–6:
[...] Punnett's square seems to have been a development of 1905, too late for the first edition of his Mendelism (May 1905) but much in evidence in Report III to the Evolution Committee of the Royal Society [(Bateson et al. 1906b) "received March 16, 1906"]. The earliest mention is contained in a letter to Bateson from Francis Galton dated October 1, 1905 (Edwards 2012). We have the testimony of Bateson (1909, p. 57) that "For the introduction of this system [the 'graphic method'], which greatly simplifies difficult cases, I am indebted to Mr. Punnett." [...] The first published diagrams appeared in 1906. [...] when Punnett published the second edition of his Mendelism, he used a slightly different format ([...] Punnett 1907, p. 45) [...] In the third edition (Punnett 1911, p. 34) he reverted to the arrangement [...] with a description of the construction of what he called the "chessboard" method (although in truth it is more like a multiplication table). [...]
(11 pages) - ^ Wimsatt, William C. (2012-05-15), "The analytic geometry of genetics: Part I: the structure, function, and early evolution of Punnett squares", Archive for History of Exact Sciences, 66 (66): 359–396 [359], doi:10.1007/s00407-012-0096-7, S2CID 119557681
- ^ Edwards, Anthony William Fairbank (June 2016). "Punnett's square: a postscript". Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences. 57. Elsevier Ltd.: 69–70. doi:10.1016/j.shpsc.2016.01.001. Retrieved 2021-03-29. (2 pages)
- ^ Müller-Wille, Staffan; Parolini, Giuditta (2020-12-09). "Punnett squares and hybrid crosses: how Mendelians learned their trade by the book". Learning by the Book: Manuals and Handbooks in the History of Science. BJHS Themes. Vol. 5. British Society for the History of Science / Cambridge University Press. pp. 149–165. doi:10.1017/bjt.2020.12. S2CID 229344415. Archived from the original on 2021-03-29. Retrieved 2021-03-29.
[...] Nilsson-Ehle was experimenting with a visual arrangement that would become very popular in Mendelian genetics. The lower half of his notes comes close to what is known as the 'Punnett square' [...] Punnett introduced this square diagram to the literature in 1906 in a paper co-authored with Bateson and Edith R. Saunders, and included it in the second edition of his Mendelism. In the third edition (1911), he added a verbal description of how to construct the diagram, and the Punnett square became a standard feature of Mendelian literature. As a detailed reconstruction by A.W.F. Edwards has shown, the diagram first took shape in an exchange of letters between Bateson and Galton for the more complex case of a trihybrid cross, and may well have been inspired by the way in which Mendel presented a case of trifactorial inheritance of flower colour in beans. [...]
- ^ Griffiths, Anthony J. F.; Miller, Jeffrey H.; Suzuki, David T.; Lewontin, Richard C.; Gelbart, William M. (2000). An Introduction to Genetic Analysis (7 ed.). New York, USA: W. H. Freeman.
- ^ Basu, Arkatappa. ""The Hindu ePaper | Daily News and Current Affairs"". epaper.thehindu.com. No. 1 April 2024. The Hindu. Retrieved 2024-04-01.
- ^ AthenaMyth (2014-06-16). "Dominant/Recessive vs Hetero/Homozygous". DeviantArt. Archived from the original on 2021-03-29. Retrieved 2017-11-19.
- ^ Shiel Jr., William C. (2018-12-12) [2017]. "Medical Definition of Hemizygous". MedicineNet. MedicineNet, Inc. Archived from the original on 2021-03-29. Retrieved 2017-11-19.
- ^ Robles, Ivan Suarez (2010-11-16). "nullizygous". Huntington's Outreach Project for Education, at Stanford (hopes). web.stanford.edu. Archived from the original on 2021-03-29. Retrieved 2017-11-19.
Further reading[edit]
- Campbell, Neil Allison (2005). Biology (7 ed.). Benjamin-Cummings Publishing Company. ISBN 978-0-8053-7146-8. OCLC 71890442.