Robertson–Wegner graph
Appearance
| Robertson–Wegner graph | |
|---|---|
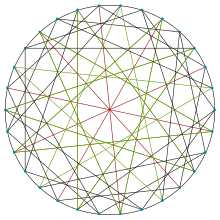 | |
| Named after | Neil Robertson |
| Vertices | 30 |
| Edges | 75 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 5 |
| Automorphisms | 20 |
| Chromatic number | 4 |
| Chromatic index | 5[1] |
| Properties | Cage |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Robertson–Wegner graph is a 5-regular undirected graph with 30 vertices and 75 edges named after Neil Robertson and Gerd Wegner.[2][3][4]
It is one of the four (5,5)-cage graphs, the others being the Foster cage, the Meringer graph, and the Wong graph.
It has chromatic number 4, diameter 3, and is 5-vertex-connected.
Algebraic properties
[edit]The characteristic polynomial of the Robertson–Wegner graph is
References
[edit]- ^ Weisstein, Eric W. "Class 2 Graph". MathWorld.
- ^ Weisstein, Eric W. "Robertson–Wegner Graph". MathWorld.
- ^ Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 238, 1976.
- ^ Wong, P. K. "A note on a paper of G. Wegner", Journal of Combinatorial Theory, Series B, 22:3, June 1977, pgs 302-303, doi:10.1016/0095-8956(77)90081-8

