Saddle point

A saddle point on the graph of z=x²−y² (in red)

Saddle point between two hills (the intersection of the figure-eight $z$-contour)

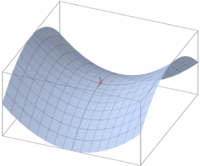
In mathematics, a saddle point is a point in the domain of a function of two variables which is a stationary point but not a local extremum. At such a point, in general, the surface resembles a saddle that curves up in one direction, and curves down in a different direction (like a horse saddle or a mountain pass). In terms of contour lines, a saddle point can be recognized, in general, by a contour that appears to intersect itself. For example, two hills separated by a high pass will show up a saddle point, at the top of the pass, like a figure-eight contour line.

Mathematical discussion

A simple criterion for checking if a given stationary point of a real-valued function F(x,y) of two real variables is a saddle point is to compute the function's Hessian matrix at that point: if the Hessian is indefinite, then that point is a saddle point. For example, the Hessian matrix of the function $z=x^{2}-y^{2}$ at the stationary point $(0,0)$ is the matrix

${\begin{bmatrix}2&0\\0&-2\\\end{bmatrix}}$

which is indefinite. Therefore, this point is a saddle point. This criterion gives only a sufficient condition. For example, the point $(0,0)$ is a saddle point for the function $z=x^{4}-y^{4},$ but the Hessian matrix of this function at the origin is the null matrix, which is not indefinite.

In the most general terms, a saddle point for a smooth function (whose graph is a curve, surface or hypersurface) is a stationary point such that the curve/surface/etc. in the neighborhood of that point is not entirely on any side of the tangent space at that point.

The plot of y = x³ with a saddle point at 0

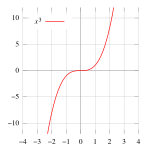
In one dimension, a saddle point is a point which is both a stationary point and a point of inflection. Since it is a point of inflection, it is not a local extremum.

Other uses

In dynamical systems, a saddle point is a periodic point whose stable and unstable manifolds have a dimension which is not zero. If the dynamic is given by a differentiable map f then a point is hyperbolic if and only if the differential of ƒ ⁿ (where n is the period of the point) has no eigenvalue on the (complex) unit circle when computed at the point.

In a two-player zero sum game defined on a continuous space, the equilibrium point is a saddle point.

A saddle point is an element of the matrix which is both the smallest element in its column and the largest element in its row.

For a second-order linear autonomous systems, a critical point is a saddle point if the characteristic equation has one positive and one negative real eigenvalue .

See also

• Saddle-point method
• Extremum
• First derivative test
• Second derivative test
• Higher order derivative test
• Saddle surface
• Hyperbolic equilibrium point

References

• Gray, Lawrence F.; Flanigan, Francis J.; Kazdan, Jerry L.; Frank, David H; Fristedt, Bert (1990), Calculus two: linear and nonlinear functions, Berlin: Springer-Verlag, pp. page 375, ISBN 0-387-97388-5 {{citation}}: |pages= has extra text (help)
• Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-1087-8
• von Petersdorff, Tobias (2006), "Critical Points of Autonomous Systems", Differential Equations for Scientists and Engineers (Math 246 lecture notes) ()
• Widder, D. V. (1989), Advanced calculus, New York: Dover Publications, pp. page 128, ISBN 0-486-66103-2 {{citation}}: |pages= has extra text (help)