Second fundamental form
In differential geometry, the second fundamental form (or shape tensor) is a quadratic form on the tangent plane of a smooth surface in the three-dimensional Euclidean space, usually denoted by (read "two"). Together with the first fundamental form, it serves to define extrinsic invariants of the surface, its principal curvatures. More generally, such a quadratic form is defined for a smooth immersed submanifold in a Riemannian manifold.
Surface in R3[edit]
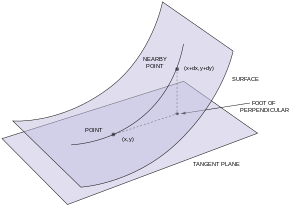
Motivation[edit]
The second fundamental form of a parametric surface S in R3 was introduced and studied by Gauss. First suppose that the surface is the graph of a twice continuously differentiable function, z = f(x,y), and that the plane z = 0 is tangent to the surface at the origin. Then f and its partial derivatives with respect to x and y vanish at (0,0). Therefore, the Taylor expansion of f at (0,0) starts with quadratic terms:
and the second fundamental form at the origin in the coordinates (x,y) is the quadratic form
For a smooth point P on S, one can choose the coordinate system so that the plane z = 0 is tangent to S at P, and define the second fundamental form in the same way.
Classical notation[edit]
The second fundamental form of a general parametric surface is defined as follows. Let r = r(u,v) be a regular parametrization of a surface in R3, where r is a smooth vector-valued function of two variables. It is common to denote the partial derivatives of r with respect to u and v by ru and rv. Regularity of the parametrization means that ru and rv are linearly independent for any (u,v) in the domain of r, and hence span the tangent plane to S at each point. Equivalently, the cross product ru × rv is a nonzero vector normal to the surface. The parametrization thus defines a field of unit normal vectors n:
The second fundamental form is usually written as
its matrix in the basis {ru, rv} of the tangent plane is
The coefficients L, M, N at a given point in the parametric uv-plane are given by the projections of the second partial derivatives of r at that point onto the normal line to S and can be computed with the aid of the dot product as follows:
For a signed distance field of Hessian H, the second fundamental form coefficients can be computed as follows:
Physicist's notation[edit]
The second fundamental form of a general parametric surface S is defined as follows.
Let r = r(u1,u2) be a regular parametrization of a surface in R3, where r is a smooth vector-valued function of two variables. It is common to denote the partial derivatives of r with respect to uα by rα, α = 1, 2. Regularity of the parametrization means that r1 and r2 are linearly independent for any (u1,u2) in the domain of r, and hence span the tangent plane to S at each point. Equivalently, the cross product r1 × r2 is a nonzero vector normal to the surface. The parametrization thus defines a field of unit normal vectors n:
The second fundamental form is usually written as
The equation above uses the Einstein summation convention.
The coefficients bαβ at a given point in the parametric u1u2-plane are given by the projections of the second partial derivatives of r at that point onto the normal line to S and can be computed in terms of the normal vector n as follows:
Hypersurface in a Riemannian manifold[edit]
In Euclidean space, the second fundamental form is given by
where is the Gauss map, and the differential of regarded as a vector-valued differential form, and the brackets denote the metric tensor of Euclidean space.
More generally, on a Riemannian manifold, the second fundamental form is an equivalent way to describe the shape operator (denoted by S) of a hypersurface,
where ∇vw denotes the covariant derivative of the ambient manifold and n a field of normal vectors on the hypersurface. (If the affine connection is torsion-free, then the second fundamental form is symmetric.)
The sign of the second fundamental form depends on the choice of direction of n (which is called a co-orientation of the hypersurface - for surfaces in Euclidean space, this is equivalently given by a choice of orientation of the surface).
Generalization to arbitrary codimension[edit]
The second fundamental form can be generalized to arbitrary codimension. In that case it is a quadratic form on the tangent space with values in the normal bundle and it can be defined by
where denotes the orthogonal projection of covariant derivative onto the normal bundle.
In Euclidean space, the curvature tensor of a submanifold can be described by the following formula:
This is called the Gauss equation, as it may be viewed as a generalization of Gauss's Theorema Egregium.
For general Riemannian manifolds one has to add the curvature of ambient space; if N is a manifold embedded in a Riemannian manifold (M,g) then the curvature tensor RN of N with induced metric can be expressed using the second fundamental form and RM, the curvature tensor of M:
See also[edit]
- First fundamental form
- Gaussian curvature
- Gauss–Codazzi equations
- Shape operator
- Third fundamental form
- Tautological one-form
References[edit]
- Guggenheimer, Heinrich (1977). "Chapter 10. Surfaces". Differential Geometry. Dover. ISBN 0-486-63433-7.
- Kobayashi, Shoshichi & Nomizu, Katsumi (1996). Foundations of Differential Geometry, Vol. 2 (New ed.). Wiley-Interscience. ISBN 0-471-15732-5.
- Spivak, Michael (1999). A Comprehensive introduction to differential geometry (Volume 3). Publish or Perish. ISBN 0-914098-72-1.
External links[edit]
- Steven Verpoort (2008) Geometry of the Second Fundamental Form: Curvature Properties and Variational Aspects from Katholieke Universiteit Leuven.




















