Algorithm for binary prefix code
In information theory, Shannon–Fano–Elias coding is a precursor to arithmetic coding, in which probabilities are used to determine codewords.[1] It is named for Claude Shannon, Robert Fano, and Peter Elias.
Algorithm description
[edit]Given a discrete random variable X of ordered values to be encoded, let  be the probability for any x in X. Define a function
be the probability for any x in X. Define a function

Algorithm:
- For each x in X,
- Let Z be the binary expansion of
 .
.
- Choose the length of the encoding of x,
 , to be the integer
, to be the integer 
- Choose the encoding of x,
 , be the first
, be the first  most significant bits after the decimal point of Z.
most significant bits after the decimal point of Z.
Let X = {A, B, C, D}, with probabilities p = {1/3, 1/4, 1/6, 1/4}.
- For A

- In binary, Z(A) = 0.0010101010...

- code(A) is 001
- For B

- In binary, Z(B) = 0.01110101010101...

- code(B) is 011
- For C

- In binary, Z(C) = 0.101010101010...

- code(C) is 1010
- For D

- In binary, Z(D) = 0.111

- code(D) is 111
Shannon–Fano–Elias coding produces a binary prefix code, allowing for direct decoding.
Let bcode(x) be the rational number formed by adding a decimal point before a binary code. For example, if code(C) = 1010 then bcode(C) = 0.1010. For all x, if no y exists such that

then all the codes form a prefix code.
By comparing F to the CDF of X, this property may be demonstrated graphically for Shannon–Fano–Elias coding.
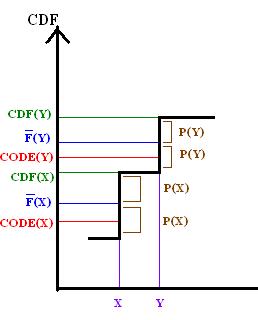
By definition of L it follows that

And because the bits after L(y) are truncated from F(y) to form code(y), it follows that

thus bcode(y) must be no less than CDF(x).
So the above graph demonstrates that the  , therefore the prefix property holds.
, therefore the prefix property holds.
The average code length is
 .
.
Thus for H(X), the entropy of the random variable X,

Shannon Fano Elias codes from 1 to 2 extra bits per symbol from X than entropy, so the code is not used in practice.





















