Parallax in astronomy

The most important fundamental distance measurements in astronomy come from trigonometric parallax, as applied in the stellar parallax method. As the Earth orbits the Sun, the position of nearby stars will appear to shift slightly against the more distant background. These shifts are angles in an isosceles triangle, with 2 AU (the distance between the extreme positions of Earth's orbit around the Sun) making the base leg of the triangle and the distance to the star being the long equal-length legs. The amount of shift is quite small, even for the nearest stars, measuring 1 arcsecond for an object at 1 parsec's distance (3.26 light-years), and thereafter decreasing in angular amount as the distance increases. Astronomers usually express distances in units of parsecs (parallax arcseconds); light-years are used in popular media.
Because parallax becomes smaller for a greater stellar distance, useful distances can be measured only for stars which are near enough to have a parallax larger than a few times the precision of the measurement. In the 1990s, for example, the Hipparcos mission obtained parallaxes for over a hundred thousand stars with a precision of about a milliarcsecond,[1] providing useful distances for stars out to a few hundred parsecs. The Hubble Space Telescope's Wide Field Camera 3 has the potential to provide a precision of 20 to 40 microarcseconds, enabling reliable distance measurements up to 5,000 parsecs (16,000 ly) for small numbers of stars.[2][3] The Gaia space mission provided similarly accurate distances to most stars brighter than 15th magnitude.[4]
Distances can be measured within 10% as far as the Galactic Center, about 30,000 light years away. Stars have a velocity relative to the Sun that causes proper motion (transverse across the sky) and radial velocity (motion toward or away from the Sun). The former is determined by plotting the changing position of the stars over many years, while the latter comes from measuring the Doppler shift of the star's spectrum caused by motion along the line of sight. For a group of stars with the same spectral class and a similar magnitude range, a mean parallax can be derived from statistical analysis of the proper motions relative to their radial velocities. This statistical parallax method is useful for measuring the distances of bright stars beyond 50 parsecs and giant variable stars, including Cepheids and the RR Lyrae variables.[5]


The motion of the Sun through space provides a longer baseline that will increase the accuracy of parallax measurements, known as secular parallax. For stars in the Milky Way disk, this corresponds to a mean baseline of 4 AU per year, while for halo stars the baseline is 40 AU per year. After several decades, the baseline can be orders of magnitude greater than the Earth–Sun baseline used for traditional parallax. However, secular parallax introduces a higher level of uncertainty because the relative velocity of observed stars is an additional unknown. When applied to samples of multiple stars, the uncertainty can be reduced; the uncertainty is inversely proportional to the square root of the sample size.[8]
Moving cluster parallax is a technique where the motions of individual stars in a nearby star cluster can be used to find the distance to the cluster. Only open clusters are near enough for this technique to be useful. In particular the distance obtained for the Hyades has historically been an important step in the distance ladder.
Other individual objects can have fundamental distance estimates made for them under special circumstances. If the expansion of a gas cloud, like a supernova remnant or planetary nebula, can be observed over time, then an expansion parallax distance to that cloud can be estimated. Those measurements however suffer from uncertainties in the deviation of the object from sphericity. Binary stars which are both visual and spectroscopic binaries also can have their distance estimated by similar means, and do not suffer from the above geometric uncertainty. The common characteristic to these methods is that a measurement of angular motion is combined with a measurement of the absolute velocity (usually obtained via the Doppler effect). The distance estimate comes from computing how far the object must be to make its observed absolute velocity appear with the observed angular motion.
Expansion parallaxes in particular can give fundamental distance estimates for objects that are very far, because supernova ejecta have large expansion velocities and large sizes (compared to stars). Further, they can be observed with radio interferometers which can measure very small angular motions. These combine to provide fundamental distance estimates to supernovae in other galaxies.[9] Though valuable, such cases are quite rare, so they serve as important consistency checks on the distance ladder rather than workhorse steps by themselves.
Parsec
[edit]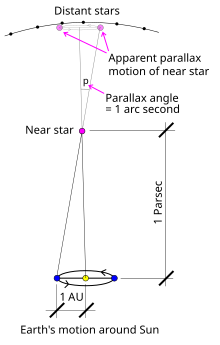
The parsec (symbol: pc) is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to 3.26 light-years or 206,265 astronomical units (AU), i.e. 30.9 trillion kilometres (19.2 trillion miles).[a] The parsec unit is obtained by the use of parallax and trigonometry, and is defined as the distance at which 1 AU subtends an angle of one arcsecond[10] (1/3600 of a degree). The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun: from that distance, the gap between the Earth and the Sun spans slightly less than 1/3600 of one degree of view.[11] Most stars visible to the naked eye are within a few hundred parsecs of the Sun, with the most distant at a few thousand parsecs, and the Andromeda Galaxy at over 700,000 parsecs.[12]
The word parsec is a portmanteau of "parallax of one second" and was coined by the British astronomer Herbert Hall Turner in 1913[13] to simplify astronomers' calculations of astronomical distances from only raw observational data. Partly for this reason, it is the unit preferred in astronomy and astrophysics, though the light-year remains prominent in popular science texts and common usage. Although parsecs are used for the shorter distances within the Milky Way, multiples of parsecs are required for the larger scales in the universe, including kiloparsecs (kpc) for the more distant objects within and around the Milky Way, megaparsecs (Mpc) for mid-distance galaxies, and gigaparsecs (Gpc) for many quasars and the most distant galaxies.
In August 2015, the International Astronomical Union (IAU) passed Resolution B2 which, as part of the definition of a standardized absolute and apparent bolometric magnitude scale, mentioned an existing explicit definition of the parsec as exactly 648000/π au, or approximately 3.0856775814913673×1016 metres (based on the IAU 2012 definition of the astronomical unit). This corresponds to the small-angle definition of the parsec found in many astronomical references.[14][15]Stellar parallax
[edit]
Stellar parallax created by the relative motion between the Earth and a star can be seen, in the Copernican model, as arising from the orbit of the Earth around the Sun: the star only appears to move relative to more distant objects in the sky. In a geostatic model, the movement of the star would have to be taken as real with the star oscillating across the sky with respect to the background stars.
Stellar parallax is most often measured using annual parallax, defined as the difference in position of a star as seen from the Earth and Sun, i.e. the angle subtended at a star by the mean radius of the Earth's orbit around the Sun. The parsec (3.26 light-years) is defined as the distance for which the annual parallax is 1 arcsecond. Annual parallax is normally measured by observing the position of a star at different times of the year as the Earth moves through its orbit. Measurement of annual parallax was the first reliable way to determine the distances to the closest stars. The first successful measurements of stellar parallax were made by Friedrich Bessel in 1838 for the star 61 Cygni using a heliometer.[16] Stellar parallax remains the standard for calibrating other measurement methods. Accurate calculations of distance based on stellar parallax require a measurement of the distance from the Earth to the Sun, now based on radar reflection off the surfaces of planets.[17]
The angles involved in these calculations are very small and thus difficult to measure. The nearest star to the Sun (and thus the star with the largest parallax), Proxima Centauri, has a parallax of 0.7687 ± 0.0003 arcsec.[18] This angle is approximate that subtended by an object 2 centimeters in diameter located 5.3 kilometers away.

The fact that stellar parallax was so small that it was unobservable at the time was used as the main scientific argument against heliocentrism during the early modern age. It is clear from Euclid's geometry that the effect would be undetectable if the stars were far enough away, but for various reasons such gigantic distances involved seemed entirely implausible: it was one of Tycho's principal objections to Copernican heliocentrism that for it to be compatible with the lack of observable stellar parallax, there would have to be an enormous and unlikely void between the orbit of Saturn (then the most distant known planet) and the eighth sphere (the fixed stars).[20]
In 1989, the satellite Hipparcos was launched primarily for obtaining improved parallaxes and proper motions for over 100,000 nearby stars, increasing the reach of the method tenfold. Even so, Hipparcos was only able to measure parallax angles for stars up to about 1,600 light-years away, a little more than one percent of the diameter of the Milky Way Galaxy. The European Space Agency's Gaia mission, launched in December 2013, can measure parallax angles to an accuracy of 10 microarcseconds, thus mapping nearby stars (and potentially planets) up to a distance of tens of thousands of light-years from Earth.[21][22] In April 2014, NASA astronomers reported that the Hubble Space Telescope, by using spatial scanning, can precisely measure distances up to 10,000 light-years away, a ten-fold improvement over earlier measurements.[19]
Diurnal parallax
[edit]Diurnal parallax is a parallax that varies with the rotation of the Earth or with a difference in location on the Earth. The Moon and to a smaller extent the terrestrial planets or asteroids seen from different viewing positions on the Earth (at one given moment) can appear differently placed against the background of fixed stars.[23][24]
The diurnal parallax has been used by John Flamsteed in 1672 to measure the distance to Mars at its opposition and through that to estimate the astronomical unit and the size of the Solar System.[25]
Lunar parallax
[edit]Lunar parallax (often short for lunar horizontal parallax or lunar equatorial horizontal parallax), is a special case of (diurnal) parallax: the Moon, being the nearest celestial body, has by far the largest maximum parallax of any celestial body, at times exceeding 1 degree.[26]
The diagram for stellar parallax can illustrate lunar parallax as well if the diagram is taken to be scaled right down and slightly modified. Instead of 'near star', read 'Moon', and instead of taking the circle at the bottom of the diagram to represent the size of the Earth's orbit around the Sun, take it to be the size of the Earth's globe, and a circle around the Earth's surface. Then, the lunar (horizontal) parallax amounts to the difference in angular position, relative to the background of distant stars, of the Moon as seen from two different viewing positions on the Earth.
One of the viewing positions is the place from which the Moon can be seen directly overhead at a given moment. That is, viewed along the vertical line in the diagram. The other viewing position is a place from which the Moon can be seen on the horizon at the same moment. That is, viewed along one of the diagonal lines, from an Earth-surface position corresponding roughly to one of the blue dots on the modified diagram.
The lunar (horizontal) parallax can alternatively be defined as the angle subtended at the distance of the Moon by the radius of the Earth[27][28]—equal to angle p in the diagram when scaled-down and modified as mentioned above.
The lunar horizontal parallax at any time depends on the linear distance of the Moon from the Earth. The Earth-Moon linear distance varies continuously as the Moon follows its perturbed and approximately elliptical orbit around the Earth. The range of the variation in linear distance is from about 56 to 63.7 Earth radii, corresponding to a horizontal parallax of about a degree of arc, but ranging from about 61.4' to about 54'.[26] The Astronomical Almanac and similar publications tabulate the lunar horizontal parallax and/or the linear distance of the Moon from the Earth on a periodical e.g. daily basis for the convenience of astronomers (and of celestial navigators), and the study of how this coordinate varies with time forms part of lunar theory.

Parallax can also be used to determine the distance to the Moon.
One way to determine the lunar parallax from one location is by using a lunar eclipse. A full shadow of the Earth on the Moon has an apparent radius of curvature equal to the difference between the apparent radii of the Earth and the Sun as seen from the Moon. This radius can be seen to be equal to 0.75 degrees, from which (with the solar apparent radius of 0.25 degrees) we get an Earth apparent radius of 1 degree. This yields for the Earth-Moon distance 60.27 Earth radii or 384,399 kilometres (238,854 mi) This procedure was first used by Aristarchus of Samos[29] and Hipparchus, and later found its way into the work of Ptolemy.[30]
The diagram at the right shows how daily lunar parallax arises on the geocentric and geostatic planetary model, in which the Earth is at the center of the planetary system and does not rotate. It also illustrates the important point that parallax need not be caused by any motion of the observer, contrary to some definitions of parallax that say it is, but may arise purely from motion of the observed.
Another method is to take two pictures of the Moon at the same time from two locations on Earth and compare the positions of the Moon relative to the stars. Using the orientation of the Earth, those two position measurements, and the distance between the two locations on the Earth, the distance to the Moon can be triangulated:

This is the method referred to by Jules Verne in his 1865 novel From the Earth to the Moon:
Until then, many people had no idea how one could calculate the distance separating the Moon from the Earth. The circumstance was exploited to teach them that this distance was obtained by measuring the parallax of the Moon. If the word parallax appeared to amaze them, they were told that it was the angle subtended by two straight lines running from both ends of the Earth's radius to the Moon. If they had doubts about the perfection of this method, they were immediately shown that not only did this mean distance amount to a whole two hundred thirty-four thousand three hundred and forty-seven miles (94,330 leagues) but also that the astronomers were not in error by more than seventy miles (≈ 30 leagues).
Solar parallax
[edit]After Copernicus proposed his heliocentric system, with the Earth in revolution around the Sun, it was possible to build a model of the whole Solar System without scale. To ascertain the scale, it is necessary only to measure one distance within the Solar System, e.g., the mean distance from the Earth to the Sun (now called an astronomical unit, or AU). When found by triangulation, this is referred to as the solar parallax, the difference in position of the Sun as seen from the Earth's center and a point one Earth radius away, i.e., the angle subtended at the Sun by the Earth's mean radius. Knowing the solar parallax and the mean Earth radius allows one to calculate the AU, the first, small step on the long road of establishing the size and expansion age[31] of the visible Universe.
A primitive way to determine the distance to the Sun in terms of the distance to the Moon was already proposed by Aristarchus of Samos in his book On the Sizes and Distances of the Sun and Moon. He noted that the Sun, Moon, and Earth form a right triangle (with the right angle at the Moon) at the moment of first or last quarter moon. He then estimated that the Moon–Earth–Sun angle was 87°. Using correct geometry but inaccurate observational data, Aristarchus concluded that the Sun was slightly less than 20 times farther away than the Moon. The true value of this angle is close to 89° 50', and the Sun is about 390 times farther away.[29]
Aristarchus pointed out that the Moon and Sun have nearly equal apparent angular sizes, and therefore their diameters must be in proportion to their distances from Earth. He thus concluded that the Sun was around 20 times larger than the Moon. This conclusion, although incorrect, follows logically from his incorrect data. It suggests that the Sun is larger than the Earth, which could be taken to support the heliocentric model.[32]

Although Aristarchus' results were incorrect due to observational errors, they were based on correct geometric principles of parallax, and became the basis for estimates of the size of the Solar System for almost 2000 years, until the transit of Venus was correctly observed in 1761 and 1769.[29] This method was proposed by Edmond Halley in 1716, although he did not live to see the results. The use of Venus transits was less successful than had been hoped due to the black drop effect, but the resulting estimate, 153 million kilometers, is just 2% above the currently accepted value, 149.6 million kilometers.
Much later, the Solar System was "scaled" using the parallax of asteroids, some of which, such as Eros, pass much closer to Earth than Venus. In a favorable opposition, Eros can approach the Earth to within 22 million kilometers.[33] During the opposition of 1900–1901, a worldwide program was launched to make parallax measurements of Eros to determine the solar parallax[34] (or distance to the Sun), with the results published in 1910 by Arthur Hinks of Cambridge[35] and Charles D. Perrine of the Lick Observatory, University of California.[36]
Perrine published progress reports in 1906[37] and 1908.[38] He took 965 photographs with the Crossley Reflector and selected 525 for measurement.[39] A similar program was then carried out, during a closer approach, in 1930–1931 by Harold Spencer Jones.[40] The value of the Astronomical Unit (roughly the Earth-Sun distance) obtained by this program was considered definitive until 1968, when radar and dynamical parallax methods started producing more precise measurements.
Also radar reflections, both off Venus (1958) and off asteroids, like Icarus, have been used for solar parallax determination. Today, use of spacecraft telemetry links has solved this old problem. The currently accepted value of solar parallax is 8.794143 arcseconds.[41]
Moving-cluster parallax
[edit]The open stellar cluster Hyades in Taurus extends over such a large part of the sky, 20 degrees, that the proper motions as derived from astrometry appear to converge with some precision to a perspective point north of Orion. Combining the observed apparent (angular) proper motion in seconds of arc with the also observed true (absolute) receding motion as witnessed by the Doppler redshift of the stellar spectral lines, allows estimation of the distance to the cluster (151 light-years) and its member stars in much the same way as using annual parallax.[42]
Dynamical parallax
[edit]Dynamical parallax has sometimes also been used to determine the distance to a supernova when the optical wavefront of the outburst is seen to propagate through the surrounding dust clouds at an apparent angular velocity, while its true propagation velocity is known to be the speed of light.[43]
Spatio-temporal parallax
[edit]From enhanced relativistic positioning systems, spatio-temporal parallax generalizing the usual notion of parallax in space only has been developed. Then, event fields in spacetime can be deduced directly without intermediate models of light bending by massive bodies such as the one used in the PPN formalism for instance.[44]
Statistical parallax
[edit]Two related techniques can determine the mean distances of stars by modelling the motions of stars. Both are referred to as statistical parallaxes, or individually called secular parallaxes and classical statistical parallaxes.
The motion of the Sun through space provides a longer baseline that will increase the accuracy of parallax measurements, known as secular parallax. For stars in the Milky Way disk, this corresponds to a mean baseline of 4 AU per year. For halo stars the baseline is 40 AU per year. After several decades, the baseline can be orders of magnitude greater than the Earth–Sun baseline used for traditional parallax. Secular parallax introduces a higher level of uncertainty, because the relative velocity of other stars is an additional unknown. When applied to samples of multiple stars, the uncertainty can be reduced; the precision is inversely proportional to the square root of the sample size.[8]
The mean parallaxes and distances of a large group of stars can be estimated from their radial velocities and proper motions. This is known as a classical statistical parallax. The motions of the stars are modelled to statistically reproduce the velocity dispersion based on their distance.[8][45]
Other methods for distance measurement in astronomy
[edit]In astronomy, the term "parallax" has come to mean a method of estimating distances, not necessarily utilizing a true parallax, such as:
See also
[edit]Notes
[edit]- ^ One trillion here is short scale, ie. 1012 (one million million, or billion in long scale).
References
[edit]- ^ Perryman, M. A. C.; et al. (1999). "The HIPPARCOS Catalogue". Astronomy and Astrophysics. 323: L49–L52. Bibcode:1997A&A...323L..49P.
- ^ Harrington, J. D.; Villard, R. (10 April 2014). "NASA's Hubble Extends Stellar Tape Measure 10 Times Farther Into Space". NASA. Archived from the original on 17 February 2019. Retrieved 17 October 2014.
- ^ Riess, A. G.; Casertano, S.; Anderson, J.; MacKenty, J.; Filippenko, A. V. (2014). "Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope". The Astrophysical Journal. 785 (2): 161. arXiv:1401.0484. Bibcode:2014ApJ...785..161R. doi:10.1088/0004-637X/785/2/161. S2CID 55928992.
- ^ Brown, A. G. A.; et al. (Gaia collaboration) (August 2018). "Gaia Data Release 2: Summary of the contents and survey properties". Astronomy & Astrophysics. 616. A1. arXiv:1804.09365. Bibcode:2018A&A...616A...1G. doi:10.1051/0004-6361/201833051.
- ^ B., Baidyanath (2003). An Introduction to Astrophysics. PHI Learning Private Limited. ISBN 978-81-203-1121-3.
- ^ "Hubble finds Universe may be expanding faster than expected". Archived from the original on 11 September 2018. Retrieved 3 June 2016.
- ^ "Hubble stretches the stellar tape measure ten times further". ESA/Hubble Images. Archived from the original on October 30, 2017. Retrieved April 12, 2014.
- ^ a b c Popowski, P.; Gould, A. (1998). "Mathematics of Statistical Parallax and the Local Distance Scale". arXiv:astro-ph/9703140.
- ^ Bartel, N.; et al. (1994). "The shape, expansion rate and distance of supernova 1993J from VLBI measurements". Nature. 368 (6472): 610–613. Bibcode:1994Natur.368..610B. doi:10.1038/368610a0. S2CID 4316734.
- ^ "Cosmic Distance Scales – The Milky Way". Retrieved 24 September 2014.
- ^ Benedict, G. F.; et al. "Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri" (PDF). Proceedings of the HST Calibration Workshop. pp. 380–384. Retrieved 11 July 2007.
- ^ "Farthest Stars". StarDate. University of Texas at Austin. 15 May 2021. Retrieved 5 September 2021.
- ^ Dyson, F. W. (March 1913). "The distribution in space of the stars in Carrington's Circumpolar Catalogue". Monthly Notices of the Royal Astronomical Society. 73 (5): 342. Bibcode:1913MNRAS..73..334D. doi:10.1093/mnras/73.5.334.
[paragraph 14, page 342] Taking the unit of distance R* to be that corresponding to a parallax of 1″·0 [… Footnote:]
* There is need for a name for this unit of distance. Mr. Charlier has suggested Siriometer, but if the violence to the Greek language can be overlooked, the word Astron might be adopted. Professor Turner suggests Parsec, which may be taken as an abbreviated form of "a distance corresponding to a parallax of one second". - ^ Cox, Arthur N., ed. (2000). Allen's Astrophysical Quantities (4th ed.). New York: AIP Press / Springer. Bibcode:2000asqu.book.....C. ISBN 978-0387987460.
- ^ Binney, James; Tremaine, Scott (2008). Galactic Dynamics (2nd ed.). Princeton, NJ: Princeton University Press. Bibcode:2008gady.book.....B. ISBN 978-0-691-13026-2.
- ^ Zeilik & Gregory 1998, p. 44.
- ^ Zeilik & Gregory 1998, § 22-3.
- ^ Benedict, G. Fritz, et al. (1999). "Interferometric Astrometry of Proxima Centauri and Barnard's Star Using Hubble Space Telescope Fine Guidance Sensor 3: Detection Limits for Substellar Companions". The Astronomical Journal. 118 (2): 1086–1100. arXiv:Astro-ph/9905318. Bibcode:1999AJ....118.1086B. doi:10.1086/300975. S2CID 18099356.
- ^ a b Harrington, J.D.; Villard, Ray (10 April 2014). "NASA's Hubble Extends Stellar Tape Measure 10 Times Farther Into Space". NASA. Archived from the original on 12 April 2014. Retrieved 11 April 2014.
- ^ Dobrzycki, J. (1973). Dobrzycki, Jerzy (ed.). The Reception of Copernicus' Heliocentric Theory. p. 51. doi:10.1007/978-94-015-7614-7. ISBN 978-90-481-8340-1.
- ^ "Soyuz ST-B successfully launches Gaia space observatory". nasaspaceflight.com. 19 December 2013. Archived from the original on 19 December 2013. Retrieved 19 December 2013.
- ^ Henney, Paul J. "ESA's Gaia Mission to study stars". Astronomy Today. Archived from the original on 2008-03-17. Retrieved 2008-03-08.
- ^ Seidelmann, P. Kenneth (2005). Explanatory Supplement to the Astronomical Almanac. University Science Books. pp. 123–125. ISBN 978-1-891389-45-0.
- ^ Barbieri, Cesare (2007). Fundamentals of astronomy. CRC Press. pp. 132–135. ISBN 978-0-7503-0886-1.
- ^ Van Helden, A. (2010). Measuring the universe: cosmic dimensions from Aristarchus to Halley. University of Chicago Press. Ch. 12.
- ^ a b "D". The Astronomical Almanac. [Department of Defense] Navy Department, Naval Observatory, Nautical Almanac Office. 1981.
- ^ The Astronomical Almanac. [Department of Defense] Navy Department, Naval Observatory, Nautical Almanac Office. 1981. p. M10.
- ^ United States Naval Observatory. Nautical Almanac Office; Great Britain. Nautical Almanac Office (2006). Explanatory Supplement to the Astronomical Almanac. University Science Books. p. 125. ISBN 978-1-891389-45-0.
- ^ a b c Gutzwiller, Martin C. (1998). "Moon–Earth–Sun: The oldest three-body problem". Reviews of Modern Physics. 70 (2): 589–639. Bibcode:1998RvMP...70..589G. doi:10.1103/RevModPhys.70.589.
- ^ Webb, Stephen (1999), "3.2 Aristarchus, Hipparchus, and Ptolemy", Measuring the Universe: The Cosmological Distance Ladder, Springer, pp. 27–35, ISBN 9781852331061. See in particular p. 33: "Almost everything we know about Hipparchus comes down to us by way of Ptolemy."
- ^ Freedman, W.L. (2000). "The Hubble constant and the expansion age of the Universe". Physics Reports. 333 (1): 13–31. arXiv:astro-ph/9909076. Bibcode:2000PhR...333...13F. doi:10.1016/S0370-1573(00)00013-2. S2CID 413222.
- ^ Al-Khalili, Jim (2010), Pathfinders: The Golden Age of Arabic Science, Penguin UK, p. 270, ISBN 9780141965017, archived from the original on 2015-03-17,
Some have suggested that his calculation of the relative size of the earth and sun led Aristarchus to conclude that it made more sense for the earth to be moving around the much larger sun than the other way round.
- ^ Whipple 2007, p. 47.
- ^ Newcomb, Simon (1911). . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 20 (11th ed.). Cambridge University Press. p. 761.
- ^ Hinks, Arthur R. (1909). "Solar Parallax Papers No. 7: The General Solution from the Photographic Right Ascensions of Eros, at the Opposition of 1900". Monthly Notices of the Royal Astronomical Society. 69 (7): 544–67. Bibcode:1909MNRAS..69..544H. doi:10.1093/mnras/69.7.544.
- ^ Perrine, Charles D. (1910). Determination of the solar parallax from photographs of Eros made with the Crossley reflector of the Lick Observatory University of California (First ed.). Washington, D. C.: Carnegie Institution of Washington. pp. 1–104.
- ^ Perrine, C. D. (1906). "The Measurement and Reduction of the Photographs of Eros Made With the Crossley Reflector in 1900". Publications of the Astronomical Society of the Pacific. 18 (10): 226.
- ^ Perrine, Charles D. (1908). "Progress on the Crossley Eros Solar Parallax Work". Publications of the Astronomical Society of the Pacific. 20 (120): 184. Bibcode:1908PASP...20..184P. doi:10.1086/121816. S2CID 121782316.
- ^ Campbell, W. W. (1906). "Reports of the Observatories: Lick Observatory". Publications of the Astronomical Society of the Pacific. 19 (113): 92.
- ^ Jones, H. Spencer (1941). "The Solar Parallax and the Mass of the Moon from Observations of Eros at the Opposition of 1931". Mem. Roy. Astron. Soc. 66: 11–66.
- ^ "Astronomical Constants" (PDF). US Naval Observatory. Archived from the original (PDF) on 2011-07-20.
- ^ Vijay K. Narayanan; Andrew Gould (1999). "A Precision Test of Hipparcos Systematics toward the Hyades". The Astrophysical Journal. 515 (1): 256. arXiv:astro-ph/9808284. Bibcode:1999ApJ...515..256N. doi:10.1086/307021. S2CID 15351552.
- ^ Panagia, N.; Gilmozzi, R.; MacChetto, F.; Adorf, H.-M.; et al. (1991). "Properties of the SN 1987A circumstellar ring and the distance to the Large Magellanic Cloud". The Astrophysical Journal. 380: L23. Bibcode:1991ApJ...380L..23P. doi:10.1086/186164.
- ^ Rubin, J.L. (2015). "Relativistic Pentametric Coordinates from Relativistic Localizing Systems and the Projective Geometry of the Spacetime Manifold". Electronic Journal of Theoretical Physics. 12 (32): 83–112. Archived from the original on 2015-02-08.
- ^ Layden, Andrew C; Hanson, Robert B; Hawley, Suzanne L; Klemola, Arnold R; Hanley, Christopher J (1996). "The Absolute Magnitude and Kinematics of RR Lyrae Stars Via Statistical Parallax". The Astronomical Journal. 112: 2110. arXiv:astro-ph/9608108. Bibcode:1996AJ....112.2110L. doi:10.1086/118167. S2CID 8732647.

