Szemerédi regularity lemma

In extremal graph theory, Szemerédi’s regularity lemma states that a graph can be partitioned into a bounded number of parts so that the edges between parts are regular. The lemma shows that certain properties of random graphs can be applied to dense graphs like counting the copies of a given subgraph within graphs. Endre Szemerédi proved the lemma over bipartite graphs for his theorem on arithmetic progressions in 1975 and for general graphs in 1978. Variants of the lemma use different notions of regularity and apply to other mathematical objects like hypergraphs.
Statement[edit]
To state Szemerédi's regularity lemma formally, we must formalize what the edge distribution between parts behaving 'almost randomly' really means. By 'almost random', we're referring to a notion called ε-regularity. To understand what this means, we first state some definitions. In what follows G is a graph with vertex set V.
Definition 1. Let X, Y be disjoint subsets of V. The edge density of the pair (X, Y) is defined as:
where E(X, Y) denotes the set of edges having one end vertex in X and one in Y.
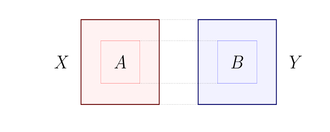
We call a pair of parts ε-regular if, whenever you take a large subset of each part, their edge density isn't too far off the edge density of the pair of parts. Formally,
Definition 2. For ε > 0, a pair of vertex sets X and Y is called ε-regular, if for all subsets A ⊆ X, B ⊆ Y satisfying |A| ≥ ε|X|, |B| ≥ ε|Y|, we have
The natural way to define an ε-regular partition should be one where each pair of parts is ε-regular. However, some graphs, such as the half graphs, require many pairs of partitions (but a small fraction of all pairs) to be irregular.[1] So we shall define ε-regular partitions to be one where most pairs of parts are ε-regular.
Definition 3. A partition of into sets is called an -regular partition if
Now we can state the lemma:
Szemerédi's Regularity Lemma. For every ε > 0 and positive integer m there exists an integer M such that if G is a graph with at least M vertices, there exists an integer k in the range m ≤ k ≤ M and an ε-regular partition of the vertex set of G into k sets.
The bound M for the number of parts in the partition of the graph given by the proofs of Szemeredi's regularity lemma is very large, given by a O(ε−5)-level iterated exponential of m. At one time it was hoped that the true bound was much smaller, which would have had several useful applications. However Gowers (1997) found examples of graphs for which M does indeed grow very fast and is at least as large as a ε−1/16-level iterated exponential of m.[2]
Proof[edit]

We shall find an ε-regular partition for a given graph following an algorithm:
- Start with a partition
- While the partition isn't ε-regular:
- Find the subsets which witness ε-irregularity for each irregular pair.
- Refine the partition using all the witnessing subsets.
We apply a technique called the energy increment argument to show that this process stops after a bounded number of steps. To do this, we define a measure which must increase by a certain amount in each step, but it's bounded above and thus cannot increase indefinitely. This measure is called 'energy' as it's an quantity.
Definition 4. Let U, W be subsets of V. Set . The energy of the pair (U, W) is defined as:
For partitions of U and of W, we define the energy to be the sum of the energies between each pair of parts:
Finally, for a partition of V, define the energy of to be . Specifically,
Note that energy is between 0 and 1 because edge density is bounded above by 1:
Now, we start by proving that energy does not decrease upon refinement.
Lemma 1. (Energy is nondecreasing under partitioning) For any partitions and of vertex sets and , .
Proof: Let and . Choose vertices uniformly from and uniformly from , with in part and in part . Then define the random variable . Let us look at properties of . The expectation is
The second moment is
By convexity, . Rearranging, we get that for all .
If each part of is further partitioned, the new partition is called a refinement of . Now, if , applying Lemma 1 to each pair proves that for every refinement of , . Thus the refinement step in the algorithm doesn't lose any energy.
Lemma 2. (Energy boost lemma) If is not -regular as witnessed by , then,
Proof: Define as above. Then,
But observe that with probability (corresponding to and ), so
Now we can prove the energy increment argument, which shows that energy increases substantially in each iteration of the algorithm.
Lemma 3 (Energy increment lemma) If a partition of is not -regular, then there exists a refinement of where every is partitioned into at most parts such that
Proof: For all such that is not -regular, find and that witness irregularity (do this simultaneously for all irregular pairs). Let be a common refinement of by 's. Each is partitioned into at most parts as desired. Then,
Where is the partition of given by . By Lemma 1, the above quantity is at least
Since is cut by when creating , so is a refinement of . By lemma 2, the above sum is at least
But the second sum is at least since is not -regular, so we deduce the desired inequality.
Now, starting from any partition, we can keep applying Lemma 3 as long as the resulting partition isn't -regular. But in each step energy increases by , and it's bounded above by 1. Then this process can be repeated at most times, before it terminates and we must have an -regular partition.
Applications[edit]
Graph counting lemma[edit]
If we have enough information about the regularity of a graph, we can count the number of copies of a specific subgraph within the graph up to small error.
Graph Counting Lemma. Let be a graph with , and let . Let be an -vertex graph with vertex sets such that is -regular whenever . Then, the number of labeled copies of in is within of
This can be combined with Szemerédi's regularity lemma to prove the Graph removal lemma. The graph removal lemma can be used to prove Roth's Theorem on Arithmetic Progressions,[3] and a generalization of it, the hypergraph removal lemma, can be used to prove Szemerédi's theorem.[4]
The graph removal lemma generalizes to induced subgraphs, by considering edge edits instead of only edge deletions. This was proved by Alon, Fischer, Krivelevich, and Szegedy in 2000.[5] However, this required a stronger variation of the regularity lemma.
Szemerédi's regularity lemma does not provide meaningful results in sparse graphs. Since sparse graphs have subconstant edge densities, -regularity is trivially satisfied. Even though the result seems purely theoretical, some attempts [6][7] have been made to use the regularity method as compression technique for large graphs.
Frieze-Kannan regularity[edit]
A different notion of regularity was introduced by Frieze and Kannan, known as the weak regularity lemma.[8] This lemma defines a weaker notion of regularity than that of Szemerédi which uses better bounds and can be used in efficient algorithms.
Given a graph , a partition of its vertices is said to be Frieze-Kannan -regular if for any pair of sets :
The weak regularity lemma for graphs states that every graph has a weak -regular partition into at most parts.
This notion can be extended to graphons by defining a stepping operator. Given a graphon and a partition of , we can define as a step-graphon with steps given by and values given by averaging over each step.
A partition is weak -regular if:
The weak regularity lemma for graphons states that every graphon has a weak -regular partition into at most parts. As with Szemerédi's regularity lemma, the weak regularity also induces a counting lemma.
Algorithmic applications[edit]
One of the initial motivations for the development of the weak regularity lemma was the search for an efficient algorithm for estimating the maximum cut in a dense graph.[8] It has been shown that approximating the max-cut problem beyond 16/17 is NP-hard,[9] however an algorithmic version of the weak regularity lemma gives an efficient algorithm for approximating the max-cut for dense graphs within an additive error.[8] These ideas have been further developed into efficient sampling algorithms for estimating max-cut in dense graphs.[10]
The smaller bounds of the weak regularity lemma allow for efficient algorithms to find an -regular partition.[11] Graph regularity has further been used in various area of theoretical computer science, such as matrix multiplication[12] and communication complexity.[13]
Strong regularity lemma[edit]
The strong regularity lemma is a stronger variation of the regularity lemma proven by Alon, Fischer, Krivelevich, and Szegedy in 2000.[5] Intuitively, it provides information between non-regular pairs and could be applied to prove the induced graph removal lemma.
Statement[edit]
For any infinite sequence of constants , there exists an integer such that for any graph , we can obtain two (equitable) partitions and such that the following properties are satisfied:
- refines , that is every part of is the union of some collection of parts in .
- is -regular and is -regular.
Proof[edit]
We apply the regularity lemma repeatedly to prove the stronger version. A rough outline:
- Start with be an regular partition
- Repeatedly find its refinement that is regular. If the energy increment of , we simply return . Otherwise, we replace with and continue.
We start with be an regular partition of with parts. Here corresponds to the bound of parts in regularity lemma when .
Now for , we set to be an regular refinement of with parts. By the energy increment argument, . Since the energy is bounded in , there must be some such that . We return as .
By our choice of the regular and refinement conditions hold. The energy condition holds trivially. Now we argue for the number of parts. We use induction to show that , there exists such that . By setting , we have . Note that when , , so we could set and the statement is true for . By setting , we have
Remarks on equitable[edit]
A partition is equitable if the sizes of any two sets differ by at most . By equitizing in each round of iteration, the proof of regularity lemma could be accustomed to prove the equitable version of regularity lemma. And by replacing the regularity lemma with its equitable version, the proof above could prove the equitable version of strong regularity lemma where and are equitable partitions.
A useful corollary[edit]
Statement[edit]
For any infinite sequence of constants , there exists such that there exists a partition and subsets for each where the following properties are satisfied:
- is -regular for each pair
- for all but pairs
Motivation[edit]
The corollary explores deeper the small energy increment. It gives us a partition together with subsets with large sizes from each part, which are pairwise regular. In addition, the density between the corresponding subset pairs differs "not much" from the density between the corresponding parts.
Proof of corollary[edit]
We'll only prove the weaker result where the second condition only requires to be -regular for . The full version can be proved by picking more subsets from each part that are mostly pairwise regular and combine them together.
Let . We apply the strong regularity lemma to find equitable that is a regular partition and equitable that is a regular refinement of , such that and .
Now assume that , we randomly pick a vertex from each and let to be the set that contains in . We argue that the subsets satisfy all the conditions with probability .
By setting the first condition is trivially true since is an equitable partition. Since at most vertex pairs live between irregular pairs in , the probability that the pair and is irregular , by union bound, the probability that at least one pair , is irregular . Note that
So by Markov's inequality , so with probability , at most pairs could have . By union bound, the probability that all conditions hold .
History and extensions[edit]

Szemerédi (1975) first introduced a weaker version of this lemma, restricted to bipartite graphs, in order to prove Szemerédi's theorem,[14] and in (Szemerédi 1978) he proved the full lemma.[15] Extensions of the regularity method to hypergraphs were obtained by Rödl and his collaborators[16][17][18] and Gowers.[19][20]
János Komlós, Gábor Sárközy and Endre Szemerédi later (in 1997) proved in the blow-up lemma[21][22] that the regular pairs in Szemerédi regularity lemma behave like complete bipartite graphs under the correct conditions. The lemma allowed for deeper exploration into the nature of embeddings of large sparse graphs into dense graphs.
The first constructive version was provided by Alon, Duke, Lefmann, Rödl and Yuster.[23] Subsequently, Frieze and Kannan gave a different version and extended it to hypergraphs.[24] They later produced a different construction due to Alan Frieze and Ravi Kannan that uses singular values of matrices.[25] One can find more efficient non-deterministic algorithms, as formally detailed in Terence Tao's blog[26] and implicitly mentioned in various papers.[27][28][29]
An inequality of Terence Tao extends the Szemerédi regularity lemma, by revisiting it from the perspective of probability theory and information theory instead of graph theory.[30] Terence Tao has also provided a proof of the lemma based on spectral theory, using the adjacency matrices of graphs.[31]
It is not possible to prove a variant of the regularity lemma in which all pairs of partition sets are regular. Some graphs, such as the half graphs, require many pairs of partitions (but a small fraction of all pairs) to be irregular.[1]
It is a common variant in the definition of an -regular partition to require that the vertex sets all have the same size, while collecting the leftover vertices in an "error"-set whose size is at most an -fraction of the size of the vertex set of .
A stronger variation of the regularity lemma was proven by Alon, Fischer, Krivelevich, and Szegedy while proving the induced graph removal lemma. This works with a sequence of instead of just one, and shows that there exists a partition with an extremely regular refinement, where the refinement doesn't have too large of an energy increment.
Szemerédi's regularity lemma can be interpreted as saying that the space of all graphs is totally bounded (and hence precompact) in a suitable metric (the cut distance). Limits in this metric can be represented by graphons; another version of the regularity lemma simply states that the space of graphons is compact.[32]
References[edit]
- ^ a b Conlon, David; Fox, Jacob (2012), "Bounds for graph regularity and removal lemmas", Geometric and Functional Analysis, 22 (5): 1191–1256, arXiv:1107.4829, doi:10.1007/s00039-012-0171-x, MR 2989432, S2CID 1623986
- ^ Gowers, W. T. (1997), "Lower bounds of tower type for Szemerédi's uniformity lemma", Geometric and Functional Analysis, 7 (2): 322–337, doi:10.1007/PL00001621, MR 1445389, S2CID 115242956
- ^ Roth, K. F. (1953), "On certain sets of integers", Journal of the London Mathematical Society, 28 (1): 104–109, doi:10.1112/jlms/s1-28.1.104, MR 0051853
- ^ Tao, Terence (2006), "A variant of the hypergraph removal lemma", Journal of Combinatorial Theory, Series A, 113 (7): 1257–1280, arXiv:math/0503572, doi:10.1016/j.jcta.2005.11.006, MR 2259060, S2CID 14337591
- ^ a b Alon, Noga; Fischer, Eldar; Krivelevich, Michael; Szegedy, Mario (2000), "Efficient testing of large graphs", Combinatorica, 20 (4): 451–476, doi:10.1007/s004930070001, MR 1804820, S2CID 44645628
- ^ Pelosin, Francesco (2018), Graph Compression Using The Regularity Method (MSc thesis), Ca' Foscari University of Venice, arXiv:1810.07275
- ^ Fiorucci, Marco; Pelosin, Francesco; Pelillo, Marcello (February 2020), "Separating structure from noise in large graphs using the regularity lemma", Pattern Recognition, 98: 107070, arXiv:1905.06917, Bibcode:2020PatRe..9807070F, doi:10.1016/j.patcog.2019.107070, S2CID 155100313
- ^ a b c Frieze, Alan; Kannan, Ravi (1999), "Quick Approximation to Matrices and Applications", Combinatorica, 19 (2): 175–220, doi:10.1007/s004930050052, S2CID 15231198
- ^ Håstad, Johan (2001), "Some Optimal Inapproximability Results", Journal of the ACM, 48 (4): 798–859, doi:10.1145/502090.502098, S2CID 5120748
- ^ Alon, Noga; Fernandez de la Vega, W.; Kannan, Ravi; Karpinksi, Marek (2003), "Random sampling and approximation of MAX-CSPs", Journal of Computer and System Sciences, 67 (2): 212–243, doi:10.1016/S0022-0000(03)00008-4, S2CID 34786604
- ^ Dellamonica, Domingos; Kalyanasundaram, Subrahmanyam; Martin, Daniel; Rödl, Vojtěch; Shapira, Asaf (2012), "Random sampling and approximation of MAX-CSPs", SIAM Journal on Discrete Mathematics, 26 (1): 15–29, doi:10.1137/110846373
- ^ Bansal, Nikhil; Williams, Ryan (2009), "Regularity Lemmas and Combinatorial Algorithms", 2009 50th Annual IEEE Symposium on Foundations of Computer Science, pp. 745–754, doi:10.1109/FOCS.2009.76, ISBN 978-1-4244-5116-6
- ^ Hajnal, András; Maass, Wolfgang; Turán, Gyorgy (1988), "On the Communication Complexity of Graph Properties", Proceedings of the twentieth annual ACM symposium on Theory of computing - STOC '88, vol. 26, Association for Computing Machinery, pp. 186–191, doi:10.1145/62212.62228, ISBN 0897912640, S2CID 17495443
- ^ Szemerédi, Endre (1975), "On sets of integers containing no k elements in arithmetic progression", Polska Akademia Nauk. Instytut Matematyczny. Acta Arithmetica, 27: 199–245, doi:10.4064/aa-27-1-199-245, MR 0369312.
- ^ Szemerédi, Endre (1978), "Regular partitions of graphs", Problèmes combinatoires et théorie des graphes (Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976), vol. 260, Paris: CNRS, pp. 399–401, MR 0540024.
- ^ Frankl, Peter; Rödl, Vojtěch (2002), "Extremal problems on set systems", Random Structures & Algorithms, 20 (2): 131–164, doi:10.1002/rsa.10017.abs, MR 1884430.
- ^ Rödl, Vojtěch; Skokan, Jozef (2004), "Regularity lemma for k-uniform hypergraphs", Random Structures & Algorithms, 25 (1): 1–42, doi:10.1002/rsa.20017, MR 2069663, S2CID 7458739.
- ^ Nagle, Brendan; Rödl, Vojtěch; Schacht, Mathias (2006), "The counting lemma for regular k-uniform hypergraphs", Random Structures & Algorithms, 28 (2): 113–179, CiteSeerX 10.1.1.378.8503, doi:10.1002/rsa.20117, MR 2198495, S2CID 14126774.
- ^ Gowers, W. T. (2006), "Quasirandomness, counting and regularity for 3-uniform hypergraphs", Combinatorics, Probability and Computing, 15 (1–2): 143–184, doi:10.1017/S0963548305007236, MR 2195580, S2CID 14632612.
- ^ Gowers, W. T. (2007), "Hypergraph regularity and the multidimensional Szemerédi theorem", Annals of Mathematics, Second Series, 166 (3): 897–946, arXiv:0710.3032, Bibcode:2007arXiv0710.3032G, doi:10.4007/annals.2007.166.897, MR 2373376, S2CID 56118006.
- ^ Komlós, János; Sárközy, Gábor N.; Szemerédi, Endre (1997), "Blow-up lemma", Combinatorica, 17 (1): 109–123, doi:10.1007/BF01196135, MR 1466579, S2CID 6720143
- ^ Komlós, János; Sárközy, Gábor N.; Szemerédi, Endre (1998), "An algorithmic version of the blow-up lemma", Random Structures & Algorithms, 12 (3): 297–312, arXiv:math/9612213, doi:10.1002/(SICI)1098-2418(199805)12:3<297::AID-RSA5>3.3.CO;2-W, MR 1635264
- ^ Alon, N.; Duke, R. A.; Lefmann, H.; Rödl, V.; Yuster, R. (1994), "The algorithmic aspects of the regularity lemma", Journal of Algorithms, 16: 80–109, CiteSeerX 10.1.1.102.681, doi:10.1006/jagm.1994.1005
- ^ Frieze, Alan M.; Kannan, Ravi (1996), "The regularity lemma and approximation schemes for dense problems", 37th Annual Symposium on Foundations of Computer Science, FOCS '96, Burlington, Vermont, USA, 14–16 October, 1996, IEEE Computer Society, pp. 12–20, doi:10.1109/SFCS.1996.548459, ISBN 0-8186-7594-2, S2CID 38681854
- ^ Frieze, Alan; Kannan, Ravi (March 1999), "A simple algorithm for constructing Szemerédi's regularity partition", The Electronic Journal of Combinatorics, 6 (1), Article R17, doi:10.37236/1449
- ^ Tao, Terence (2009), Szemeredi's regularity lemma via random partitions
- ^ Alon, Noga; Shapira, Asaf (2008), "Every monotone graph property is testable", SIAM J. Comput., 38 (2): 505–522, doi:10.1137/050633445, ISSN 0097-5397, MR 2411033
- ^ Ishigami, Yoshiyasu (2006), A Simple Regularization of Hypergraphs, arXiv:math/0612838, Bibcode:2006math.....12838I
- ^ Austin, Tim (2008), "On exchangeable random variables and the statistics of large graphs and hypergraphs", Probability Surveys, 5: 80–145, arXiv:0801.1698, Bibcode:2008arXiv0801.1698A, doi:10.1214/08-PS124, S2CID 15421306
- ^ Tao, Terence (2006), "Szemerédi's regularity lemma revisited", Contributions to Discrete Mathematics, 1 (1): 8–28, arXiv:math/0504472, Bibcode:2005math......4472T, doi:10.11575/cdm.v1i1.61900, MR 2212136.
- ^ Tao, Terence (2012), The spectral proof of the Szemeredi regularity lemma
- ^ Lovász, László; Szegedy, Balázs (2007), "Szemerédi's lemma for the analyst", Geometric and Functional Analysis, 17: 252–270, doi:10.1007/s00039-007-0599-6, ISSN 1016-443X, MR 2306658, S2CID 15201345
Further reading[edit]
- Komlós, J.; Simonovits, M. (1996), "Szemerédi's regularity lemma and its applications in graph theory", Combinatorics, Paul Erdős is eighty, Vol. 2 (Keszthely, 1993), Bolyai Soc. Math. Stud., vol. 2, János Bolyai Math. Soc., Budapest, pp. 295–352, MR 1395865.
- Komlós, J.; Shokoufandeh, Ali; Simonovits, Miklós; Szemerédi, Endre (2002), "The regularity lemma and its applications in graph theory", Theoretical aspects of computer science (Tehran, 2000), Lecture Notes in Computer Science, vol. 2292, Springer, Berlin, pp. 84–112, doi:10.1007/3-540-45878-6_3, ISBN 978-3-540-43328-6, MR 1966181.
External links[edit]
- Edmonds, Chelsea; Koutsoukou-Argyraki, Angeliki; Paulson, Lawrence C. Szemerédi's regularity lemma (Formal proof development in Isabelle/HOL, Archive of Formal Proofs)





























![{\displaystyle \mathbb {E} [Z]=\sum _{i=1}^{k}\sum _{j=1}^{l}{\frac {|U_{i}|}{|U|}}{\frac {|W_{j}|}{|W|}}d(U_{i},W_{j})={\frac {e(U,W)}{|U||W|}}=d(U,W)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b77fc7d2a081235a50ec404c0f5b8d86a8fb46f8)
![{\displaystyle \mathbb {E} [Z^{2}]=\sum _{i=1}^{k}\sum _{j=1}^{l}{\frac {|U_{i}|}{|U|}}{\frac {|W_{j}|}{|W|}}d(U_{i},W_{j})^{2}={\frac {n^{2}}{|U||W|}}q({\mathcal {P}}_{U},{\mathcal {P}}_{W})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d271858bc72e3e79441afb4c0c5404d9b63cd0d)
![{\displaystyle \mathbb {E} [Z^{2}]\geq \mathbb {E} [Z]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d79f576f4150c8614c5109e9e4bf6bc65451b62)









![{\displaystyle Var(Z)=\mathbb {E} [Z^{2}]-\mathbb {E} [Z]^{2}={\frac {n^{2}}{|U||W|}}\left(q\left(\{U_{1},U\backslash U_{1}\},\{W_{1},W\backslash W_{1}\}\right)-q(U,W)\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4258194fbe62a2e241e50ae9024874a4f39c1367)
![{\displaystyle |Z-\mathbb {E} [Z]|=|d(U_{1},W_{1})-d(U,W)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4376d2a3c82c0bc04cbe2e6f94e0551ef1ad091c)



![{\displaystyle Var(Z)=\mathbb {E} [(Z-\mathbb {E} [Z])^{2}]\geq {\frac {|U_{1}|}{|U|}}{\frac {|W_{1}|}{|W|}}(d(U_{1},W_{1})-d(U,W))^{2}>\varepsilon \cdot \varepsilon \cdot \varepsilon ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/306baad32de89198b78249c16ed6f4737f37a392)









![{\displaystyle q({\mathcal {Q}})=\sum _{(i,j)\in [k]^{2}}q({\mathcal {Q}}_{V_{i}},{\mathcal {Q}}_{V_{j}})=\sum _{(V_{i},V_{j}){\text{ }}\varepsilon {\text{-regular}}}q({\mathcal {Q}}_{V_{i}},{\mathcal {Q}}_{V_{j}})+\sum _{(V_{i},V_{j}){\text{ not }}\varepsilon {\text{-regular}}}q({\mathcal {Q}}_{V_{i}},{\mathcal {Q}}_{V_{j}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0154b1fb8af2d877216e0c057aa00242f13e5f2)



![{\displaystyle \sum _{(i,j)\in [k]^{2}}q(V_{i},V_{j})+\sum _{(V_{i},V_{j}){\text{ not }}\varepsilon {\text{-regular}}}\varepsilon ^{4}{\frac {|V_{i}||V_{j}|}{n^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bde1973f5fb4547ffaf03514ae6dd134f42aa12)



![{\displaystyle V(H)=[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45b5e6e0d4a785cf98ab990e18739013b7a091cd)












![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

































































