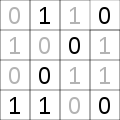
Takuzu
The topic of this article may not meet Wikipedia's general notability guideline. (July 2015) |
Takuzu, also known as Binairo, is a logic puzzle involving placement of two symbols, often 1s and 0s, on a rectangular grid. The objective is to fill the grid with 1s and 0s, where there is an equal number of 1s and 0s in each row and column and no more than two of either number adjacent to each other. Additionally, there can be no identical rows or columns. Similar to Sudoku, each puzzle begins with several squares in the grid already filled.
Names and variations
[edit]The game is known as Binairo, Takuzu, Binero,[1][2] Tohu-Wa-Vohu (Formless and Empty), Eins und Zwei (One and Two), Binary Puzzles, Binoxxo, Zernero,[3] Tic-Tac-Logic,[4] and Sudoku Binary.[5] The names "Binairo" and "Takuzu" are trademarked in the European Union.[6][7] The name "Binero" is trademarked in France by Editions Megastar.[8] LinkedIn publishes a version of this game as well, called Tango.[9]
Certain names imply specific symbols being used. For example, Binary Puzzles use 1s and 0s (i.e. binary numbers), Tic-Tac-Logic uses Xs and Os (like tic-tac-toe), Eins und Zwei uses 1s and 2s, and Tohu-Wa-Vohu uses T and V symbols. However, many of the names are used for any variation of symbols. Black and white circles (or squares) are another commonly used pair of symbols. Any variation of two numbers, letters, colors, or pictures can work as the two symbols, though it is generally common for the symbols to be 1s, Xs, or shapes.
The rectangular grid sizes can vary greatly. Since the objective is to have equal number of both symbols in each row and column, the number of rows and columns is normally even. Though not required, grids are often square. Common sizes range from 4x4 to 20x20.[10][11] Larger puzzles are also made, including ones that use a 30x40 grid.[12]
Some variations allow identical rows and columns.[3] Another variation, Odd Binairo, has an odd number of rows and columns with each containing one more 1 than 0s (i.e. in a 11x11 grid, each row and column has 5 zeros and 6 ones).[13]
History
[edit]There are two competing origins to the puzzle, both created around the same time. Tohu wa Vohu was invented by Italian Adolfo Zanellati.[3] Binairo was created by Belgians Peter De Schepper and Frank Coussement in 2009.[1][13]
Tic-Tac-Logic claims its origin on creating a single-player version of tic-tac-toe. Like tic-tac-toe, it uses Xs and Os. The two-player game's goal is to create three in a row, while in Tic-Tac-Logic, the goal is to prevent any three in a row.[4]
Solving methods
[edit]-
An unsolved 4×4 Takuzu grid
-
The same grid, solved
- Each row and each column must contain an equal number of 0s and 1s. Therefore, if the required number of 0s or 1s is reached in a row or a column, the remaining cells must contain the other digit (1xx101 → 100101).
- More than two of the same digits can't be adjacent. Therefore, if two adjacent cells contain the same digit, the cells next to the digits must contain the other digit (xxx00x → xx1001). Likewise, if two cells contain the same digit with one empty cell in between, this empty cell must contain the other digit, because otherwise three same digit appears (x1x1xx → x101xx).
- Eliminate the impossible. For example, if the sixth cell in 110xxx is made a 1, balancing the number of 0s and 1s forces a trio to appear (110xxx → 110xx1 → 110001), so it can't be a 1. Therefore, the sixth cell must contain a 0 (110xxx → 110xx0).
- Each row and column is unique (100101 & 1001xx → 100101 & 100110).
Mathematics
[edit]A zero-knowledge proof for the puzzle was published in Jun 2016.[14][15]
The puzzle was adapted for modeling quantum agents.[16]
Mathematicians of Dutch university (PH Utomo and RH Makarim) proposed three different approaches to solve binary puzzles: using backtrack-based search, SAT solvers, and Gröbner bases algorithms.[17] The last two approaches reduce the problem of solving a binary puzzle to a Boolean satisfiability problem and solving systems of polynomial equations over the binary field.
References
[edit]- ^ a b Aberkane, Idriss J. (18 July 2016). "Comment le Binairo stimule les neurones !" [How Binairo stimulates neurons!]. Le Point (in French). Retrieved 9 February 2019.
- ^ Cusset, Maïlys (23 June 2016). "Binairo, le jeu pour les accros des chiffres" [Binairo, the game for number addicts]. Biba (in French). Retrieved 9 February 2019.
- ^ a b c "Tohu-Wa-Vohu". janko.at (in German). Retrieved 9 February 2019.
- ^ a b "Tic-Tac-Logic history". Conceptis Puzzles. Retrieved 9 February 2019.
- ^ "Sudoku Binary - Google Search". www.google.com.
- ^ "EUTM file information - Binairo". EUIPO. Retrieved 9 February 2019.
- ^ "EUTM file information - Takuzu". EUIPO. Retrieved 9 February 2019.
- ^ "BINERO RELAX (Marques) - Data INPI". data.inpi.fr.
- ^ "LinkedIn goes deeper into puzzle games with Tango, following success of Queens". cnbc.com. Retrieved 17 October 2024.
- ^ "Binairo". Binairo. Puzzle Team. Retrieved 9 February 2019.
- ^ "Binary Puzzle". BinaryPuzzle.com. Retrieved 9 February 2019.
- ^ "Special Monthly Binairo". Binairo. Puzzle Team. Retrieved 9 February 2019.
- ^ a b "Even and Odd Binairo". PeterFrank. Retrieved 9 February 2019.
- ^ Bultel, Xavier; Dreier, Jannik; Dumas, Jean-Guillaume; Lafourcade, Pascal (2016). "Physical Zero-Knowledge Proofs for Akari, Takuzu, Kakuro and KenKen". arXiv:1606.01045 [cs.CR].
- ^ Xavier Bultel, Jannik Dreier, Jean-Guillaume Dumas, and Pascal Lafourcade4. "Physical Zero-Knowledge Proofs for Akari, Takuzu, Kakuro and KenKen" (PDF).
{{cite web}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link) - ^ Fougères, Alain-Jérôme (2017). "Agent Having Quantum Properties: The Superposition States and the Entanglement". Computational Collective Intelligence. Lecture Notes in Computer Science. Vol. 10448. pp. 389–398. doi:10.1007/978-3-319-67074-4_38. ISBN 978-3-319-67073-7.
- ^ Utomo, Putranto H.; Makarim, Rusydi H. (2017). "Solving a Binary Puzzle". Mathematics in Computer Science. 11 (3–4): 515–526. doi:10.1007/s11786-017-0322-4.
External links
[edit]