Talk:Geometric algebra/Archive 2

Archive 1

Archive 2

Archive 3

Archive 4

Emil Artin

Not that I have anything against Hestenes-worshippers (I met Hestenes once and he's a nice guy, if a little bit ..... well, let me put it this way: I think he said Clifford algebras will settle all questions of physics, or something like that) .... OK, where was I? Oh: Well doesn't Emil Artin also warrant some attention on this page? -- Mike Hardy - 131.183.73.24 (contributions) 02:13, 25 February 2003 (UTC)

He has his reasons for saying that. The formalism he's helped developed for geometric algebra has been applied to electromagnetics, relativity, gauge theory, analytical mechanics, quantum mechanics and quantum computing. It easily subsumes both complex analysis and quaternions,and it eliminates the need for matrix manipulations - and their associated coordinate systems - in order to rotate, mirror, or project objects in space. It can do this because it is algebraic. Intermediate calculations/transformations don't reference any coordinates. That comes at the end, when it's time to figure out what the geometric transformation looks like in a chosen coordinate system.

If you do modern physics, you want a coordinate free mathematics. You also want the ability to use your tools beyond 2D and 3D. Geometric algebra does just that, extending cleanly into n dimensions.

My impression is that Hestenes cares little about worship. He's been quoted - often - about getting people's name off of the work of what is a broad community of contributors. Thus his adoption of Clifford's own term for this field - geometric algebra. Clifford himself was very open about his debt to Grassmann. ColdSun (talk) 19:33, 24 October 2011 (UTC)

How comes that geometric algebra and Clifford algebra are not synonyms?

Here's what is written in the History section:

(Clifford's) "contribution was to define a new product — the geometric product — on an existing Grassmann algebra, which realized the quaternions as living within that algebra"

This statement generates a doubt. Here's how I interpret it:

• (Original) Clifford algebras. Clifford introduced only a subset of what are now called the "Clifford algebras". This subset is currently called "geometric algebras".
• Generalized Clifford algebras. Later, someone else generalized Clifford algebras, and the resulting set was called "Clifford algebras".

Is my interpretation correct? If it is correct, how comes that geometric algebra and Clifford algebra are not synonyms? Why did that happen? Isn't there some better terminology in the literature? Isn't it desirable to clarify this point in the history section?

Paolo.dL 18:14, 26 July 2007 (UTC)

This is a good question – what’s the distinction? – and confused me as well. As near as I can tell, geometric algebra is the interpretation of and application of (nondegenerate) Clifford algebras to geometry, especially at the elementary level of an alternative to vector algebra; mathematically, it’s a branch of the theory of Clifford algebra, and that’s how it’s linked from Clifford algebra.

There are many topics in Clifford algebras that aren’t of (direct) geometric relevance, such as the Classification of Clifford algebras or representation theory (spinors); this article seems strictly about the generalization of vector algebra and the basic products – does this sound right to you?

—Nils von Barth (nbarth) (talk) 07:24, 14 February 2010 (UTC)

Geometric algebra uses both the Clifford (geometric) and Grassmann (wedge) products, as well as various inner products, such as the Hestenes' and left and right contractions, in a system designed to facilitate calculation, and retain geometric insight. The Clifford algebras themselves are exactly that: associative algebras over a field, that is a vector space over a field with an associative product, in this case, the Clifford product. That is why you see statements like: such and such a Clifford algebra is isomorphic to a real matrix algebra, a Clifford algebra is Z/2Z graded etc. A Clifford algebra can be constructed via a quadratic form over an n-dimensional base vector space via a map, sometimes called a Clifford map, which maps the vectors in the n-dimensional base space into the 2^n-dimensional Clifford algebra. This extra structure induces a grading. The Grassmann algebras are also associative algebras over a field. Geometric algebra combines all these structures into one system, starting from an n-dimensional base space, defining a Clifford map into a 2^n dimensional space, and defining all the relevant products on that space in a consistent manner, so that the grading makes sense. Penguian (talk) 15:20, 17 March 2011 (UTC)

Software list needs updating?

The software section could stand being brought up to date. Besides the GluCat library (more than 9 years old), there is Gaalet and there are more recent offerings. Penguian (talk) —Preceding undated comment added 15:44, 17 March 2011 (UTC).

typo?

I'm a newbie, but in the Notation and Definitions section, quote:

"The outer product of n vectors produces a pseudoscalar I. The inner product can also be generalised:-...

decomposing the geometric product of a vector with a k-blade into a (k − 1)-blade and a (k + 1)-blade ."

shouldn't "the outer product..." and "the inner product..." read "the inner product..." and "the geometric product..." respectively?

DrTechDaddy (talk) 22:00, 6 October 2011 (UTC)

It is correct, although it misses out a lot of explanation. It would not make sense to add such detail though as the article is already on the long side, and besides in a definition section too much explanation can make it more difficult to find the facts. You might be better trying one of the references or further reading links, for something which covers it in more detail.--JohnBlackburne^words_deeds 22:12, 6 October 2011 (UTC)

Thanks for the clarification. I suppose I was confused by the term "pseudoscalar". DrTechDaddy (talk) 14:31, 7 October 2011 (UTC)

Distinction between GA and Clifford Algebra

It is not made clear, either in the article on Clifford algebras (CA) or this one on GA, what the distinction is (except perhaps that GA is assigned a geometric interpretation and that it is typically restricted to being over a real vector space). Something that has perplexed me in trying to apply my concept of a (real) Clifford Algebra when trying to understand GA is that I kept drawing clearly incorrect conclusions from the symmetries present in a CA. I think I have finally worked out why this is, and this perspective may be valuable if highlighted in this article on GA. In a nutshell, GA identifies a subspace that it calls 1-vectors, whereas CA does not, and this has many implications. It means that CA has far greater symmetry than GA does, and the two are thus not equivalent. I guess GA may be considered to be a proper subalgebra of the corresponding CA, formed by adding the identification of the 1-vector subspace. In general a Cl_n(R) may have any n of several possible combinations of its 2ⁿ basis elements chosen as the generating basis, with the structure being isomorphic between such choices. In particular, we can typically find a set of n Clifford elements that do not all have the same grade (as seen from the perspective of our first CA), but are mutually anti-commuting and have the original signature. As an example, in C_0,2(R) i.e. quaternions, we can choose (e₁, e₂), (e₁, e₁e₂) or (e₂, e₁e₂). We can use these n elements to generate the same algebra, only with what is the space spanned by the generating elements (the new "1-vector subspace") being of mixed grade from the original perspective. Thus the concept of "grade" has no real sense in a CA, but it has very real meaning in GA. This allows several concepts in GA that have little or no meaning in CA: vectors, bivectors, rotors, versors etc. In short, any non-scalar grade-specific concept. Does anyone support me on adding a section on this? And can anyone suggest references that might deal with this? (Perhaps "Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry" by Leo Dorst et al mentions this?) – Quondum (talk) 10:09, 14 July 2011 (UTC)

I don't have reference materials with me at the moment to quote exactly what whichever authorities say, but my understanding is that "a Geometric algebra is a Clifford algebra with a particular geometric interpretation attached to it".

As far as I remember, when I was first introduced to GA (when the founders of the Cambridge GA group were just getting interested in it), "Geometric Algebra" was used as an umbrella name for the whole field, while the particular individual algebras were just called Clifford Algebras. If you look back at literature from the period, I think that will be reflected; it was also how this article was written until not so very long ago (the article Hypercomplex number still is), with the various algebras denoted as Cℓ_3,0(R) etc.

As for choosing different elements as the basis for the underlying "flat" that the algebra is contructed from, I suppose you mean something like the fact that eg the same algebra, the coquaternions can represent either Cℓ_1,1(R) or Cℓ_2,0(R) depending which elements you take for the basis elements of grade-1. But despite being element-wise isomorphic in this way, I think those two are identified as different Clifford algebras.

It is an interesting point that, for example in Cℓ_3,0(R), you could multiply each grade-1 basis vector through by the pseudoscalar to obtain a corresponding bivector, which originally you could have chosen as your first three elements and then built a Clifford algebra out of. But I don't think it actually opens up so much daylight between the CA and the GA. The CA is an abstract structure -- it has elements, that combine in such-and-such a way, to produce such-and-such a multiplication table. What it is that GA adds (I think) is the identification that those grade-1 elements that seed the algebra are going to be interpreted as spatial vectors; rather than interpreting them physically as bivectors, or (as you suggest) as some additive combination of a particular vector and a particular bivector; or as something else entirely.

It's interesting that you have the impression that CA is somehow more general than GA. But, apart from the fact that one might choose a different physical identification for the CA's grade-1 elements (or even no physical identification at all), I don't think the CA does have any more generality than the corresponding GA. (So I don't see any particular reason to denote the GA as ${\mathcal {G}}_{3,0}$ rather than Cℓ_3,0(R)).

It's possible some mathematicians may be under the impression that GAs are less general than CA, because in GA the objects of most physical interest tend to be pure blades, or (if they are mixed) pure bivectors; with grade-tracking also so important in doing calculations efficiently. But to take that distinction too seriously I think is a mistake. Mixed-grade objects certainly can come up in GAs, and GA equations, even if they can be a challenge to interpret.

That's my understanding, anyway. I should make the disclaimer that I am at best only an occasional distant intrigued observer of the GA scene, certainly not a practised practitioner, so anything I write should be given no more credence than it deserves. Jheald (talk) 16:13, 14 July 2011 (UTC)

I should perhaps start with a similar disclaimer: I am interested dabbler, and what I say on the subject is certainly not to be taken as gospel.

Contrary to your perspective, I would suggest that isomorphic algebras are to be regarded as the same algebra; what path one followed to find for example the multiplication table does not distinguish one algebra from its isomorphic twin. This would lead me to suggest that it makes no sense to call Cℓ_2,0(R) "different" from Cℓ_1,1(R) - these are merely labels that record how we derived the algebra; once we discover them to be isomorphic (not only element-wise, but for all operations), they are in a very real sense the same algebra. Anyway, that is the perspective that I am working from; we can let the mathematicians decide.

Given this perspective, until we add something to a GA to distinguish it mathematically (and adding physical interpretation does not do so), it "is" a CA. What I am saying is that the concept of a grade-preserving operation such as a rotor cannot be defined in a pure CA - it only preserves grade when this is defined in terms of a privileged basis. Choosing another basis to define what are vectors does not change the CA in any way, but somehow changes what is or is not a rotor, vector, blade, etc. Put another way: present someone with the multiplication table for a CA, and they will be able to perform addition, subtraction, multiplication and division; but they will not be able to find inner or outer products, or to identify vectors, blades, rotors etc. Thus, I am suggesting that what we think of as a GA including rotors etc. only makes sense when defined as a CA with a specified 1-vector subspace. It is a CA with its symmetry broken by means of this additional item of information. This subspace cannot be identified uniquely from the CA multiplication table. (Aside: A Grassmann algebra is inherently graded, unlike a CA, and hence like a GA has less symmetry.)

Confusing all this is that the Clifford algebras article (and probably much of the literature) leans so heavily on the construction and analysis by use of grading that one implicitly assumes that it is inherent or given. Or perhaps I am misunderstanding it and the CA definition includes specification of the 1-vector subspace, but then we need to define the super-CA without this specification as a mathematically relevant concept. – Quondum (talk) 20:09, 14 July 2011 (UTC)

I think CAs are understood to be graded algebras, so the specification of a set of elements as belonging to grade-1 is part of the specification of the algebra; so, for that reason, Cℓ_2,0(R) is not equivalent to Cℓ_1,1(R), even though there is an isomorphism between them.

But I did learn about GAs before I learnt about CAs, so it might be that that fore-knowledge has biased what I know about CAs. Jheald (talk) 21:09, 14 July 2011 (UTC)

We seem to be in agreement that identifying the vector space is included in the definition of a GA (thus resolving what my original problem was). We seem to have changed my original question to one about the definition of CA, not about GA. I am not convinced of what you say with regard to CA, but I think that may be better dealt with by people more at home with the mathematical definition of CA.

I will add an analogy here simply to illustrate the issue for those who might be interested. Imagine generating a sphere [CA] by rotating a circle about a diameter [1-vectors]. We end up with the same sphere [what I called a super-CA above] if we use a different diameter. If we choose to insist that the definition of a "sphere" [CA] includes the identification of a special axis of rotation [1-vector subspace], we are ignoring the existence of the S₂ group, since the "sphere" with special axis only has S₁ symmetry. The S₁ symmetry preserves circles of lattitude that the S₂ symmetry does not [rotors preserve grade when restricted so by the definition of the 1-vector space]. My point is this: there is a far "bigger" super-CA that is simply being ignored if the definition of a CA includes the identification of a preferred generating subspace as its 1-vector space. This "super-CA" (e.g. coquaternions) may be used to derive many results which would then automatically apply to all the contained isomorphic CAs (e.g. Cℓ_2,0(R) and Cℓ_1,1(R)). Note also that by this definition the even subalgebra of a CA is not a CA (and not even isomorphic to one, since there is no identified subspace to be isomorphic to the 1-vectors of the similar CA). Quondum (talk) 07:04, 15 July 2011 (UTC)

There is a discussion principally between myself and Lanco Direct Construction of Grassmann, Clifford and Geometric Algebras (Arxiv) at Google Groups Difference CA and GA. This seems pretty conclusive to me, don't know whether it needs to be in the main page or not...Selfstudier (talk) 13:27, 18 October 2011 (UTC).

It would be helpful to those of us not fluent in reading mathematical papers if you actually summarized what it is you conclude so conclusively. At one point Lanco says that a CA has one product and a GA has two. Yet the paper you link to seems to define a CA W as "with an isomorphism fixing V", and it seems to me that once you have a fixed V, the Grassman product ∧_V on W is unique, essentially a contradiction. So do you conclude that a CA has no fixed V and no unique product ∧_V (making GA a CA inherently distinct classes), or that it has both (making them at least very similar)? Quondum (talk) 15:40, 18 October 2011 (UTC)

I see we are in the midst of YA attempt to turn the GA page into the CA page,I suggest amending the CA page instead (reading it properly might also be a good idea). There is actually a reason for having a GA page!Selfstudier (talk) 18:07, 29 January 2012 (UTC)

Please be clearer. "YA"? Amending the CA page in what regard? The GA page very much deserves its own existence. — Quondum^☏✎ 04:50, 30 January 2012 (UTC)

Seems to be some confusion, I am suggesting (as politely as I am able) that clarity is indeed required, just not on my part.Selfstudier (talk) 11:35, 30 January 2012 (UTC)

I've asked some specific questions that you have not answered. You've made some vague statements and not clarified upon request, nor asked questions to elicit the clarity you seek. I'm a bit at a loss. If we're to move forward from this point, I'm going to need a little help from you, aside from your muted expression of frustration. I'm not even sure this relates to the heading of this section, since there was quite a gap in time, and the timing of your post may have related to the recent edits. — Quondum^☏✎ 13:55, 30 January 2012 (UTC)

I have the impression that Clifford algebras is the term mathematicians use. "Geometric algebra" was a neologism that was coined in the 1980s or 1990s (I would have to check the sources) but has apparently become very popular among physicists. I think it amounts to much the same thing. I think it's only a question of emphasis. Tkuvho (talk) 13:59, 30 January 2012 (UTC)

Based on the edit history, the disagreement revolves around the use of the abbreviations "GA" and "CA". In both cases, it might refer to the field of study or the specific type of object. The usage I have seen indicates that geometric algebra uses both sense but, in contrast, "Clifford algebra" is usually reserved for the algebraic object only, and (so far as I have seen) rarely if ever used to name a field of study. I think the edit I'm going to do in a moment should satisfy all parties.

As for this page being "turned into" the CA page: there is no getting around the fact that geometric algebras are just special examples of Clifford algebras. The chief distinction at present seems to be that GA restricts its attention to real vector spaces, so as to model our usual three dimensional geometric sense. I think there isn't much to fear about the two pages merging anytime soon. The content of the two articles varies quite a lot, and would be a bit of a pain to merge. Rschwieb (talk) 14:23, 30 January 2012 (UTC)

The title of Snygg's new missive , "A New Approach to Differential Geometry using Clifford's Geometric Algebra" seems to encapsulate the essence of the debate....Selfstudier (talk) 14:52, 30 January 2012 (UTC)

I can't remember where I read it, but I was under the impression that Clifford initially called it "geometric algebra", and then others called it "Clifford algebra" to honor him, and then later people began to revive Clifford's usage. This might have been in Artin's "Geometric algebra" book? Rschwieb (talk) 14:58, 30 January 2012 (UTC)

Yes, he called it that in his original papers (at that time the search was for math that could usefully help with physics problems). What we now call Clifford algebra is really a generalization of the original geometric algebra.Over the years subsequent, Gibbs having won out with his vectors, the original geometric algebra was forgotten and was subsequently reinvented several times and in disguise (eg as special matrices). The difference is as much a mode of thinking as anything else, a very strict Clifford algebraic approach results in geometrical meaning being obscured. Hestenes, starting in the sixties, was the one who really revived the original (Artin was looking more at the algebra of various geometries with a somewhat different focus).Selfstudier (talk) 15:28, 30 January 2012 (UTC)

Lounesto, p 322: "Clifford coined his geometric algebra in 1876 (fist published 1878)" (formatting as in source), and makes it clear it's GA (real, non-degenrate) that Clifford was concerned with. The same history section credits Witt with extending the theory to general fields in 1937, and suggests by then they were known a Clifford algebras. It doesn't indicate when the theory was extended to include degenerate signatures.--JohnBlackburne^words_deeds 15:29, 30 January 2012 (UTC)

This page is linked to from various places (how do you find them all?). One that I have just been looking at is Algebraic structure which attempts to classify algebras according to some criteria, the composite section explicitly mentioning Clifford and Geometric algebras as Exterior algebras and describing Grassman Cayley algebra as " a geometric algebra without an inner product".Selfstudier (talk) 13:40, 31 January 2012 (UTC)

Well spotted. I'd suggest that that section needs a rewrite. The terms seem to have been confused. — Quondum^☏✎ 14:00, 31 January 2012 (UTC)

FWIW, some of the category crowd have a wiki setup intended as a repository for their still evolving ideas although their stuff on GA looks a bit dated.:-

[1] [2] [3] — Preceding unsigned comment added by Selfstudier (talk • contribs) 14:17, 31 January 2012 (UTC)

Finding links to the page? Did you try the "What links here" button?

I think the section you are referring to is a little misordered. Already in the rewriting, Q. Geometric and exterior algebras are distinct examples of the Clifford algebra construction. If Dorst is to be believed, GCA's are contained in geometric algebras, so the GA which contains it just has extra properties you don't pay attention to when considering the GCA. Rschwieb (talk) 14:20, 31 January 2012 (UTC)

You will have to forgive an oldie for not seeing it.-) I have it now, thank you (BTW, I would just like to correct your comment on Hestenes wanting to sell books, absolutely not the case, you can easily verify this if you look into the history a little bit, see what happened with his publishing efforts).

I must confess to being in two minds about all this, generalization is not always "a good thing". In this case, it was most definitely a bad thing, something which has bedeviled geometry for a long time with generalizations (Erlangen and subsequent) tending to increase complexity rather than produce the desired simplification. Likely the final words have yet to be written. — Preceding unsigned comment added by 88.82.206.110 (talk) 14:53, 31 January 2012 (UTC)

Hi, please avoid interposting... it's hard to keep track of. I didn't mean the comment on Hestenes to be a negative attack. It only looks kind of negative since GA is still relatively obscure. But if GA now became popular, he would look like a marketing genius! :) The algebraic structure page is a mess. I would never explain it to students that way. It looks like the work of engineers to me. Rschwieb (talk) 15:03, 31 January 2012 (UTC)

I like simplicity myself and Hestenes way of explaining GA still makes the most sense to me, you can find this in a paper called GrassmanLegacy or similar I think available on his site somewhere. This paper also includes a potted history.Selfstudier (talk) 15:16, 31 January 2012 (UTC)

Grassmann's legacy is the link for the above paper. — Preceding unsigned comment added by Selfstudier (talk • contribs) 15:39, 31 January 2012 (UTC)

It is worth mentioning here (if only because I do not see it mentioned very often) that CGA is in fact Mobius Geometry (there is no Wiki entry but you may find an unlinked reference to it at the opening para of Conformal_geometry and the best overall reference is perhaps Udo's Introduction to Mobius Differential Geometry. Although there is a Clifford Algebra model of Mobius Geometry, there are other models as well.Selfstudier (talk) 11:21, 1 February 2012 (UTC)

User JHeald has done some CGA work here, don't know if he intends to keep it up, last edit was August last year Jheald sandbox GA — Preceding unsigned comment added by Selfstudier (talk • contribs) 11:33, 2 February 2012 (UTC)

It would be a pity to see that go to waste. The lead is quite readible and gives a sense of what CGA is about, and the main part is clearly still a work in progress; there is a lot still to be done. I would not be able meaningfully contribute to content, but perhaps cleaning up formatting of hastily written formulae etc.? — Quondum^☏✎ 13:37, 2 February 2012 (UTC)

Feel free, jump right in; and also to use the talk page there for any critiques or suggestions, thoughts about where to go, what's not quite right, what needs to be added.

I find with GA (or CA) that it's something I have to get totally immersed in, to make progress with -- I need the luxury of being able to focus on it to the exclusion of everything else to really get to grips. So it tends to go in fits and starts, when I can afford such an encompassing enthusiasm! (But one day I will finally grok spinors, group theory, and idempotent projectors proportional to 1 + e_i )

My sense was what the sandbox CGA article really needs most is some better pictures, to better convey the mapping from R³ to CGA; how that then relates particular vectors, bivectors etc and their dual-hyperplanes to objects in R³; and with it translations and transformations etc.

It also needs somebody who's actually used it to persuasively explain why screw theory might actually be useful; i.e. why the whole thing is more than an intriguing curiosity.

I'd be as happy as anyone to see it move into mainspace. Unfortunately other stuff came up, and it wasn't yet ready for prime-time. But if anyone could help clean it up and nudge it forward to a state where you think it wouldn't be a disgrace to mainspace (even if it was still a stub), I'd be very happy. And if you could add the material that you think it needs (eg Mobius Geometry, and CGA's relation to other formulations), that would be even better.

I think it can well make it easier to develop the overlook page like this one, if pages are in place on particular target topics that detailed exposition can be deferred to using {{tl|main} templates.

Cheers, Jheald (talk) 15:52, 2 February 2012 (UTCome)

Build it and they will come.....Selfstudier (talk) 19:09, 2 February 2012 (UTC)

Also note that CGA is not CCA, it is CCA + CGCA. — Preceding unsigned comment added by Selfstudier (talk • contribs) 16:03, 5 February 2012 (UTC)

Use of direct sum ⊕ in section Pseudoscalars

As far as I can tell, ⊕ denotes direct sum of rings (also Product of rings), which is defined in a component-wise fashion, i.e. the direct-summed rings remain separable under all the defined operations (true for the complex sum, false for the complex product). The use of the symbol seems pretty variable, but there seems to be nothing in the notation R⊕iR to imply what is intended: adding of a real number to another multiplied by i. The notation iR does not even denote an algebra, but rather "the pure imaginary subspace of C". Conversely, the notation R+iR at least means "the set set of all values a+ib for all (a,b) in R×R", even if there is an implied coercion of R to C by the use of the symbol i. This is why I replaced ⊕ with +, and still feel this is appropriate. Quondum^talk_contr 15:50, 29 November 2011 (UTC)

No, the symbol ⊕ denotes direct sum in every category, not just rings. While ⊕ is correct and more specific than + (which is also correct), I'm willing to investigate which is more consistent with related articles. Looking in the most obvious places I could think of (linear span,quaternion, complex number) it seems that neither ⊕ nor + is used in this way, and that the actual setbuilder notation used in linear span would probably be the most consistent. See what you think of those modifications when I get them in. Rschwieb (talk) 18:23, 29 November 2011 (UTC)

It seems that at least we can agree upon the setbuilder notation :) Quondum^talk_contr 21:16, 29 November 2011 (UTC)

It's bulkier, but we don't need to use it very many times in the paragraph, and it leaves the least to the imaginaton. The next thing to do in that article is to make sure the sections we haven't touched are in a reasonable order. Rschwieb (talk) 23:37, 29 November 2011 (UTC)

Still on this point, I've worked out what was bothering me.

• In Classification of Clifford algebras (and in some of the rather rough definitions of Direct sum) the symbol ⊕ implies that the components of the decomposition continue to act as independent algebras for both the operations on each component ring. For example, because R has 2 idempotents, the notation R⊕R implies 2×2=4 idempotents, and R⊕R⊕R implies 2³=8 idempotents.
• The article Graded algebra uses it in an incompatible sense, where the addition remains component-wise, but the product is dictated by a separate rule combining/shuffling the components via a linear combination (with unspecified coefficients, except that it being a grading implies that in each row of the matrix all but one coefficient is zero).

It would seem that it is in this second, less precise sense that you had intended, which is equivalent to the Cartesian product with R-linearity, and a more appropriate notation for this meaning is the symbol ×. The i in iR is then merely a hint. So, more appropriately, H=R×R×R×R. Quondum^talk_contr 05:29, 30 November 2011 (UTC)

1. Yes, Classification is referring to a direct sum in the category of algebras.
2. Graded algebra says nothing incorrectly. It specifically says "A graded ring A is a ring that has a direct sum decomposition into (abelian) additive groups". (For graded algebra this is replaced with "...decomposition into subspaces"). The sum is in the category of abelian groups/vector spaces, not rings or algebras.
3. H' is isomorphic to R×R×R×R as vector spaces yes, and has a weird, non-componentwise multiplication. I think an earlier you would protest the "=" between H and this set. However H=R⊕iR⊕jR⊕kR really does indicate decomposition of H into subspaces. It's an internal direct sum. I find it unfortunate that all these symbols are so blurred; there is less difference between ⊕, ⊗ and × than between ⊕ and ⊕. Perhaps it'll be more regular in 500 years or so...

All of your confusion is caused by unfamiliarity with a host of usages involving ×, ⊕ and +, and a few other variant plusses and crosses that ambush readers. Rschwieb (talk) 17:09, 30 November 2011 (UTC)

• I was not objecting to either article; I was simply pointing out that the overloading of ⊕ had caught me (I'd understood the one article, then the other, morphing my understanding of ⊕ without realizing it, then applied the later interpretation in this article).
• (And yes, I used "=" as obviously "wrong" to make it clear insightful interpretation was needed - I'd still balk at that in an article.) I have yet to succeed in a rigorous interpretation of your expression using ⊕.
• I heartily agree with your last sentiment.
• Which comes back to my earlier point: in Wikipedia jargon and symbols must be disambiguated on the spot or avoided; I'm probably not a bad representative of the people seeing a lot of this stuff for the first time and not realizing which symbols to check for overloading or simply failing to interpret them. If I keep battling with something like this, its presentation is probably too opaque for Wikipedia. Quondum^talk_contr 19:18, 30 November 2011 (UTC)

Hestenes, Artin?

Who coined the term "geometric algebra"? I have the impression that, even if Artin used it first, Hestenes was the one who popularized it. Where did Artin use it? Some of this information should go into the article. Tkuvho (talk) 15:15, 30 January 2012 (UTC)

I see that the history section discusses Artin a bit. From what we find here it emerges that Artin used the term in a rather broad way, similar to Klein's Erlangen program. The more specific use of the term seems to be due to Hestenes. Tkuvho (talk) 15:20, 30 January 2012 (UTC)

"He [Emil Artin] wrote a book on geometric algebra that gave rise to the contemporary use of the term, reviving it from the work of W. K. Clifford." – Emil Artin#Influence and work. — Quondum^☏✎ 15:59, 30 January 2012 (UTC)

Wikipedia is not a secondary source :) Artin seems to have used the term in a broader sense than Clifford algebras. Not all of the geometries mentioned in the history section here are described by Clifford algebras. Tkuvho (talk) 16:06, 30 January 2012 (UTC)

Hestenes is certainly the loudest proponent of the term in recent times. In part, using "geometric algebra" seems like a strategem to brand the subject to seem newer/different/catchier than it used to be. It's "more oldschool" and definitely more descriptive, but part of the interest may just have been selling books and sealing his place as "the guy" for the topic. Regardless, Hestenes does not deserve credit for coining the term. Rschwieb (talk) 16:25, 30 January 2012 (UTC)

That's fine, I was just trying to put things in perspective a bit. I still have the impression that Artin was using it in a much broader sense. Clifford algebra is defined using a quadratic form, and it seems to me one doesn't get affine and projective geometries that way except in very special cases, though I have not looked at this stuff in a while and may be wrong. Could you clarify this aspect? Tkuvho (talk) 16:33, 30 January 2012 (UTC)

Clifford was the first to use the term, in both the title and content of his paper "On the classification of geometric algebras". The resurrecting of the name seems to be as Clifford algebra has been extended since Clifford's time, and 'geometric algebra' serves to distinguish the real, non-degenerate form which many find is all they need; they need not concern themselves with the more general Clifford algebra.--JohnBlackburne^words_deeds 16:54, 30 January 2012 (UTC)

Thanks for your comment. I was wondering if some of the historical material should make its way into the lede. Tkuvho (talk) 16:56, 30 January 2012 (UTC)

That would be an excellent addition. Rschwieb (talk) 17:00, 30 January 2012 (UTC)

I added a brief comment. Should we link the scholars involved? Tkuvho (talk) 15:46, 1 February 2012 (UTC)

They are already linked from the History section from their more complete names. I'd suggest that linking from their surnames in the lead may be overkill. — Quondum^☏✎ 16:08, 1 February 2012 (UTC)

I like what you've written as is, T. Rschwieb (talk) 16:37, 1 February 2012 (UTC)

I see Hestenes bashing is still a favorite distraction here. Silly rabbit has found successors ... See my remarks in "A geometric algebra bibliography" and "Remark on the history section" (February 2008 and November 2009. Before speaking, some people here should, as I did, read the early works of Hestenes. They would notice that his brilliant idea of vectorial representation of some Clifford algebras, came from the study of the Dirac equation in QM. Not only was he the first to express such an idea, but still today only a small minority of physicists accept it, in spite of its strict mathematical isomorphism with standard methods. There are not a lot of physicists having invented or reinvented mathematics which suggest strongly the necessity of reinterpreting the "Copenhague QM" ! That will be my last contrib to that subject.

Chessfan (talk) 10:40, 4 February 2012 (UTC)

Not too sure what here qualifies as "Hestenes bashing". What might be relevant to the discussion is that the use of the term "geometric algebra" by Hestenes to distinguish it as a particularly useful and intuitive (less abstract) class of algebras with direct application in physics and geometry was probably intimately tied to its modern resurgence, for which Hestenes deserves much credit. — Quondum^☏✎ 12:36, 4 February 2012 (UTC)

Hestenes is fond of talking about "Liebniz' dream" of a geometric algebra, that is an algebra where the expressions and computations directly represent geometric objects and transformations of them (also it is understood that we are talking about classical geometries). The capitalization GA arises as a matter of convenience, a shorthand way of specifying that the algebra is geometric in this sense and which was also the sense intended by Grassmann and Clifford(the idea behind CGA is similar). — Preceding unsigned comment added by Selfstudier (talk • contribs) 12:21, 5 February 2012 (UTC)

Well "bashing" is perhaps a bit strong. I do not want to offend anybody :) Chessfan (talk) 21:20, 4 February 2012 (UTC)

That's good, because based on your past informative posts, I was intending to ask you to help out at User_talk:Rschwieb/GA_Discussion, where four interested parties of different backgrounds are functioning as a learning community. Perhaps we could get in a game of chess sometime too. Have you ever played at chess.com? Rschwieb (talk) 02:25, 5 February 2012 (UTC)

Thank you for both proposals. I play usually on playchess.com, but I will try your chess.com . I will think over a contribution to your thinktank, on QM (spinors) which I already discussed with jheald somewhere. But beware I am not a theoretical oriented mathematician ; I like to simplify ! Chessfan (talk) 11:16, 5 February 2012 (UTC)

The essence of pure mathematics is to simplify :) It's a gross and widespread misconception that the opposite is true! The whole reason I'm interested in GA is to see if it is a detour around the complicated "standard course". Rschwieb (talk) 16:19, 6 February 2012 (UTC)

Article on Geometric calculus

This article and many of its references refer to geometric calculus, suggesting that such an article should exist. The existing Geometric calculus article is a disambiguation page, with only one link: to this article. I'd suggest that it should summarily be changed into a stub-class article, pending input. Geometric calculus is, after all, a rich subject area. — Quondum^☏✎ 17:50, 1 February 2012 (UTC)

A DAB page with only one item is by definition not a DAB page... Let's get the stub going. Rschwieb (talk) 18:29, 1 February 2012 (UTC)

I put a link on the talk page, not a bad place to start....Selfstudier (talk) 18:30, 2 February 2012 (UTC)

Recent revert relating to sign of n_o

[This revert] with edit caption (Undid revision 475356337 by Quondum (talk) Inner product -1? Maybe e_ first?) seems to be a misinterpretation. I changed n_o=½(e₊−e₋) to n_o=½(e₋−e₊), as is necessary to match the other identities given, including the negative dot product. It is also a direct quote from Perwass 2009 p.149 eqn 4.33 (Geometric Algebra with Applications in Engineering) that gives all the definitions and identities here (except that he uses the names e_o and e_∞). It is also identical to Hestenes's treatment (A Unified Algebraic Framework for Classical Geometry) in chapter 2. — Quondum^☏✎ 13:59, 6 February 2012 (UTC)

I have changed it to put e_ first in both expressions, is it alright now?Selfstudier (talk) 14:08, 6 February 2012 (UTC)

Yes, that corrects it. Now that you point it out, both Perwass and Hestenes put the e₋ first in both expressions, and I also prefer them to be in the same order in both expressions. I'll redo the other edits that got reverted in the process. — Quondum^☏✎ 14:19, 6 February 2012 (UTC)

Great, I remember when I did this originally there were some problems due to various groups doing it slightly differently (Dorst still does it differently in Geometric Algebra in Practice 2011).Selfstudier (talk) 14:22, 6 February 2012 (UTC)

Basically, defining the metric by R(4,1) = R(3) + R(1,1) (conformal split)Selfstudier (talk) 14:36, 6 February 2012 (UTC)

Whoops, now I'm getting confused, looking at only some of the details. It is n_o that has the minus sign. Gimme some time – I'll sort it out from the references. — Quondum^☏✎ 14:40, 6 February 2012 (UTC)

I´m reasonably sure that the way I have put it is OK (there are some different ways to get the null basis)Selfstudier (talk) 14:50, 6 February 2012 (UTC)

We might be getting in each other's way a bit here with all the changes back and forth....What are you using as the definitive reference? UAFCG?Selfstudier (talk) 15:14, 6 February 2012 (UTC)

Looking at it, I think it doesn't matter which way round it is, as long as you have 2 blades on the null cone, everything works...Selfstudier (talk) 15:36, 6 February 2012 (UTC)

I've mentioned my references above, obviously not the same as you're using. It makes sense to use a predominant convention (to minimize confusion), whichever that is. When one thinks about it, one can substitute –e₊ for e₊ throughout, and the entire theory will remain consistent, so I came to the same conclusion as you did, with the exception of the final wedge product which is as for my convention. One should never need to convert back to the original othonormal basis, and therefore the wedge product in terms of e₊ and e₋ should not be given, but will just remains as a wedge of the null vectors. So I've removed the wedge product expression, and left the rest. — Quondum^☏✎ 15:55, 6 February 2012 (UTC)

I was just going by Corrochano 2010 as mentioned in the lead-in to the section.Selfstudier (talk) 16:03, 6 February 2012 (UTC)

"Removal of Unneeded Identity" - This is in fact rather important for a proper understanding but it (and the other related useful identities) can be developed on the CGA page when it is actually up (I suggest you swipe JHealds intro and put that up, then we can start said development.-).Selfstudier (talk) 16:00, 6 February 2012 (UTC)

Yes, but that is detail needed only for understanding. I've made some edits in Jheald's sandbox, but I think you're right: development in main space is probably the way to go, as it's more likely to attract the attention of other contributing editors. I woulda liked a convention where n_∞⋅n₀=+1 as would be trivial to achieve, but I guess neither of our references do that. Do you think Jheald's sandbox page should be moved (with edit history?) or simply most of it copied to a new page Conformal geometric algebra? — Quondum^☏✎ 16:43, 6 February 2012 (UTC)

PS: I may not have access to your reference(s). Not that that will be a problem. — Quondum^☏✎ 16:46, 6 February 2012 (UTC)

Um, just copy it, I think, he might want to come back to it at some point....Selfstudier (talk) 18:00, 6 February 2012 (UTC)

Okay, I've copied it. This is an open invitation to all editors to get involved in getting the article Conformal geometric algebra written, perhaps trimming out the undeveloped stuff initially. — Quondum^☏✎ 18:50, 6 February 2012 (UTC)

Graded algebra structure

As you'll see, a graded algebra requires that the grade of the product of two elements is the sum of each of their grades. The grading that is used in GA does not exhibit this property with respect to the geometric product. It does, however, with respect to a different product: the exterior product. This should be made clear. — Quondum 14:15, 10 September 2012 (UTC)

I'll add that statement to this section, if it's ok... Maschen (talk) 15:02, 10 September 2012 (UTC)

The relationship to the exterior product might be the reason I can't see a counterexample. It sure looks graded to me. Can you give two graded elements whose product is not of the right grade? Rschwieb (talk) 15:26, 10 September 2012 (UTC)

How stupid of me... I completely overlooked the statement that the inner product is always of 0-grade... It's now reverted. (Maybe I was thinking at the time the inner product would lower the grade but not reduce it to zero... should read the articles before editing in excruciating detail next time...). Maschen (talk) 15:33, 10 September 2012 (UTC)

Disregard my request for example above! An extremely stupid example for myself: take a non-null v: then v⋅v= some nonzero scalar. Indeed, the geometric product of two 1-vectors is normally mixed! My head was totally in the exterior algebra mode, as you diagnosed. I'll make sure my mistake gets eradicated. Rschwieb (talk) 16:22, 10 September 2012 (UTC)

I think it would be logical to introduce the subject along the following lines:

The exterior algebra is naturally contained in the geometric algebra (see Clifford_algebra#Relation_to_the_exterior_algebra), with the exterior product being called the outer product in this context. The grading in GA refers to the grading of the exterior algebra. The outer product plays a substantial role in GA, having direct geometric interpretations. Using this we can define the grading operator ⟨⋅⟩_r, which may be used in defining several other operators and identities. — Quondum 16:31, 10 September 2012 (UTC)

Seems good. Is it possible to fit in close after the definition of grading? The reason I say so is that it's sometimes bad to get too far ahead of the game before the basics are defined. Even my changes to the stuff on grading should probably be migrated downward. Rschwieb (talk) 17:12, 10 September 2012 (UTC)

I thought that the exterior algebra is the natural introduction to grading (this grading is defined in terms of the exterior product and the concept of a grading is defined in terms of an algebra), and so it is natural to proceed in this order. The article currently constructs the details haphazardly (like constructing vectors out of coordinate scalars – yech), with foreknowledge of the goal. Defining grading in terms of the exterior algebra does not require orthogonal (or even any) bases. — Quondum 18:17, 10 September 2012 (UTC)

Diagrams

To the editors of this article... Some have been drawn as a result of the following interesting discussion as to how this article may be improved: User talk:Quondum#If GA is geometric, where are the diagrams!?.

From Exterior algebra... Geometric interpretation for the exterior product of n vectors (u, v, w) to obtain an n-vector (parallelotope elements), where n = grade, for n = 1, 2, 3. The "circulations" show orientation.

In 3d space, a bivector a∧b defines a 2d plane subspace (light blue, extends infinitely in indicated directions). Any vector c in the 3-space can be projected onto and rejected normal to the plane, shown respectively by c_⊥ and c_∥.

Linear transformation (first a rotation about the indicated axis, then a scaling) of top: a vector, bottom: a 3-vector; the transform of the entire 3-element corresponds to the transformation of each constituent vector from (u, v, w) to (u, v, w). A similar interpretation is true for n-vectors of higher grade.

Rotation of a unit vector v through angle θ, around the plane of the unit circle (u, w are also unit vectors and b is a unit bivector). The geometric product U_θ is called a rotor of the vectors with relative angle θ, similar to Euler's formula in the complex plane.

Reflection of vector a along a vector m.

Reflection of vector a on a vector n.

Given two vectors a and b, if the geometric product ab is anticommutative; they are perpendicular (top), if it's commutative; they are parallel (bottom).

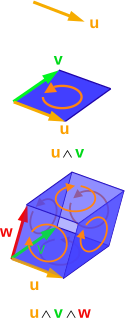
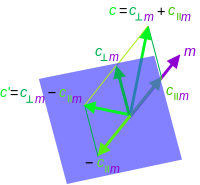
To prevent further clutter of Quondum's talk page (my fault...) it's better to place them here. Any problems/suggestions please say and I'll fix. Thank you, Maschen (talk) 17:47, 10 November 2012 (UTC)

I don't think that there is any benefit to multiple linear transforms in one diagram, we just need one that can be deduced from the diagram. That'll also reduce clutter in the diagram. — Quondum 19:01, 10 November 2012 (UTC)

So, which one to keep? R, S, or RS? Maschen (talk) 19:13, 10 November 2012 (UTC)

I went ahead to simply include rotation then scaling. Maschen (talk) 00:34, 11 November 2012 (UTC)

Yup, much better as you've changed it. Any possibility of shading faces and edges so that it is more obvious which side if the parallelopiped is closest? Perhaps also using partial transparrency. — Quondum 03:23, 11 November 2012 (UTC)

Done, anything else? Maschen (talk) 07:45, 11 November 2012 (UTC)

Well, as I see it, restructuring the Examples and applications section to give a series of clear-cut (and not verbose) geometric interpretations of objects and operations. Some is already there. The diagrams would fit into such a section. — Quondum 19:16, 12 November 2012 (UTC)

A true point, though how do you intend to re-structure? In doing so shall I transform LinePlaneIntersect.png to SVG? Maschen (talk) 19:30, 12 November 2012 (UTC)

One thing I've been meaning to diagram is a set of basis vectors, bivectors and trivector in 3-space, would that be helpful? Maschen (talk) 19:36, 12 November 2012 (UTC)

I've done a preliminary restructuring. Some expansion may be appropriate. The "Area of a parallelogram spanned..." should describe the geometric interpretation on the outer product for k dimensions, not only 2. Orientation of an n-volume in terms of that of its boundary (this is IMO a better way of understanding the orientation of a volume than using an oriented basis) may be sensible to add. Versors (rotations and refections) should be expanded to general linear transformations. But why not already add in some of the diagrams that have an obvious place? — Quondum 05:03, 13 November 2012 (UTC)

Nice start. I left them here because I wanted to be absolutely sure they are ok, though will add the obvious ones now... The orientation of an n-element via its boundary sounds good, should I incorporate that into N-vector.svg (may as well)? Maschen (talk) 07:17, 13 November 2012 (UTC)

The orientation concept will probably need a diagram of its own (preferably using a less regular shape); best experiment with that separately first rather than trying to put too much into one diagram. For now, n-vector.svg has an arrow that serves the symbolic purpose of tagging it as "oriented", which, while not ideal, is reasonably simple. — Quondum 07:43, 13 November 2012 (UTC)

Not a problem - I just drew it now, so will upload to commons and place it here. Maschen (talk) 07:59, 13 November 2012 (UTC)

Orientation of a 3-volume on its boundary.

This is clearer than a less-regular shape - you can't see orientations from behind clearly otherwise. Improvements/suggestions? Maschen (talk) 08:05, 13 November 2012 (UTC)

I guess you're right, but the concept needs to be developed separately so that this SVG is more easily understood. Have you seen Fig 12.16 in The Road to Reality? The concept works at every dimension. I would reduce the size of the circulating arrows (and possibly add some); orientation is a property at every point of the line/surface/volume. In fact, 3d orientation can also be expressed as a small circulating arrow on the surface of a small sphere in a volume; this would be the analogue if a small circulating arrow on a surface. Have you got the orientation correct in the SVG? (I'm not too sure on this one myself.) — Quondum 12:18, 13 November 2012 (UTC)

I'm with you when you say small circulating arrows on a curved surface, just didn't think of that at the time.

Yes the arrows are correct in the diagram since traversing the boundary of a boundary should result in a null path (according to MTW on some page I can't remember for now...), it concerns me when you are not sure since this implies the diagram is not clear... (Actually this version is graphically redundant to the basis vectors added earlier in section Standard bases and the geometric product, and will be redrawn soon).

I haven’t access to Penrose right now, will see to that later. Maschen (talk) 15:06, 13 November 2012 (UTC)

I'm not saying the larger circular arrows are unclear, just giving a possible alternative as per Penrose for consideration. Putting the circulating arrows on the surface has been an improvement. — Quondum 19:23, 13 November 2012 (UTC)

Here is a replacement (SVG format didn't upload properly, next best thing is PDF):

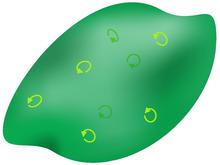
The orientation of a 3d volume may be determined by the orientation on an enclosing surface.

Maschen (talk) 20:45, 13 November 2012 (UTC)

This is a cool picture; it'll be nice for a section on orientation (on any number of dimensions), which does not yet exist. — Quondum 11:21, 14 November 2012 (UTC)

Thanks, although this isn't central to only GA I certainly do hope it enhances this article... Also added it to Orientation (geometry)#Three dimensions. Maschen (talk) 13:48, 14 November 2012 (UTC)

Here is the recoloured SVG version of Selfstudier's PNG drawing:

Maschen (talk) 21:34, 13 November 2012 (UTC)

I've not looked at this closely yet; it is about an application of GA. I do not want to do too much on these, nor allow the article to grow too much in that direction. It would potentially fall into another suite of articles (there was similar previous content moved out of this article, but I forget where to). — Quondum 11:21, 14 November 2012 (UTC)

This is not used at all, for now it's just a replacement of the PNG file and can either be taken or left. Maschen (talk) 13:48, 14 November 2012 (UTC)

Rotor diagram suggestions?

See here also. If you have any good ideas to improve the current one please post them here, and I'll tweak/redraw. One has been proposed to include reflections and commutativity/anticommutativity. Many thanks, Maschen (talk) 20:04, 18 November 2012 (UTC)

This article continues to be problematic

I'm not an expert on Geometric Algebra, but I have studied it for over a decade. I have over 225 PDFs on GA on my hard drive, about 111MB, and I have read nearly all, and re-read most. I have been dissatisfied with the WP GA article since at least 2005, (see my comment in the first archives of this page) and it doesn't seem to get much better. Although nearly every paper on every level reintroduces GA from first principles, I can think of no introduction to GA in the primary literature that is as obscure, unhelpful and poorly written as this WP article. It is so awful that anyone reading it is likely to know less about the topic than when they started. Aside from a handful of sentences and the illustrations, the entire thing needs to be scrapped and started over, instead using the introductions in the primary literature as a basis. The main problem is the turgid contributions from those who think GA is about pure math (empty symbol-shuffling and academic games) rather than a universal language for representing physical reality. Artin, quadratic forms, Bourbaki, and obscure pseudo-rigorous mathematical jargon have no place in this article. The target audience for this article should not be mathematicians, but rather high-school and undergraduate physics students. Enon (talk) 18:10, 6 May 2013 (UTC)

It's all very well stating the obvious "The target audience for this article should not be mathematicians, but rather high-school and undergraduate physics students", although it's easier said than done. Are you the driving force to improve it then? [4] Use your 225+ PDFs to rewrite instead of complaining. Feel free to criticize the diagrams as heavily as you please and I'll fix as and when. Thanks. M∧Ŝc²ħεИ_τlk 18:25, 6 May 2013 (UTC)

I have some sympathy with the complaint being made; since I ventured a major rewrite some time back, a lot of amendments have been made which don't really make the subject very easy to grasp even if the content is mathematically correct (this material tends to be skated over in the majority of readable introductions to the subject). Perhaps the meta/foundational stuff eg grading could be hived out to a separate section or something, I don't know....Selfstudier (talk) 11:40, 7 May 2013 (UTC)

@Enon We welcome constructive suggestions, but please be advised that the article will certainly not be changed to incorporate the anti-mathematical tone of your comments. I realize that was probably part of blowing off a little steam, but even so I think several of the comments are a little unfair :) Our entire understanding of what we experience is viewed through mathematical models, and it would be silly to argue that geometric algebra (a mathematical construct) is somehow "universal" ("more real"?) compared to all the other descriptions. The suggestion that quadratic forms/bilinear forms are merely "jargon" suggests that you don't appreciate that they are a cornerstone of geometry, and it is no surprise they are here.

Much literature I've read on geometric algebra written by physicists has been of the style "here are some symbols and this is how you move them, and if you do this this happens..." etc without good explanation about what's going on. I consider those to be empty symbol shuffling games, and this article comparatively more detailed.

But anyhow, we are all agreed that the article could use a lot of improvement! Maybe before the definitions section we need some brief commentary on the main interpretation(s) that make GA useful? I mean a "big picture" paragraph, to help motivate the rest of the article. Care would have to be taken to keep it simple and grounded. Rschwieb (talk) 15:26, 7 May 2013 (UTC)

Well, my post has gotten more reaction than I expected. Before getting bogged down in minutae, let me begin by saying that GA is not math. Clifford Algebra is math, and the only thing that distinguishes GA from CA is the geometric interpretation and application. To cover the same ground as the CA article is not only redundant, it obscures the purpose and meaning of GA. The criterion for judging how good the article is should be the actual increase in knowledge of the subject that it produces in the intended audience. If it isn't comprehensible to the intended audience, if it doesn't hold their interest, if it requires reading other articles that are difficult and only tangentially related, it matters not at all how rigorous or exact the GA article is - it fails in its purpose. The way people actually learn is by analogy with prior experience. We do not understand the world in terms of mathematical models - that is exactly backwards. Understanding of the physical world is prior to and the source of mathematical intuition, not derived from abstract principles. People can understand and learn the math through physical examples far more easily than they can learn anything from the typical "Bourbaki virus"-infected treatments of math (Hestenes' term). And, yes, I do maintain that Geometric Algebra is more fundamental than supposedly bedrock things like quadratic forms, linear algebra, set theory and whatnot, precisely because it requires fewer additional assumptions to accurately and generally model physical reality using GA than any of the others, and if I start from GA, I can equally or more easily deduce those other areas of math from GA than I can deduce GA from those other areas. not least because GA has physical content allowing more reliable intuition than any field that tries to be purely formal and divorced from the physical world. The article /has/ gotten better over time, but it happened in lots of little edits that left the underlying approach pretty much the same, an approach which is antithetical to the whole ethos of Geometric Algebra. Only a fresh start can fix that and give a coherent, intuition-building, application-centered approach. If an expert such as David Hestenes, Leo Dorst, or a member of the Cambridge group could be persuaded to write the article, I think that would be best. Next best would be getting permission from one or more of those authors to copy and adapt parts of the best existing introductions, or, if that isn't possible, to closely paraphrase the fairly standard approach. (Or as Tom Lehrer put it:

I am never forget the day I first meet the great Lobachevsky.

In one word he told me secret of success in mathematics:

Plagiarize!

Plagiarize,

Let no one else's work evade your eyes,

Remember why the good Lord made your eyes,

So don't shade your eyes,

But plagiarize, plagiarize, plagiarize -

...Only be sure always to call it please 'research'.

Now some minutae. A prime example of the sort of thing I'm against is the first sentence: "A geometric algebra is the Clifford algebra of a vector space over the field of real numbers endowed with a quadratic form." How could anyone object to that? Well, it manages to be obtuse, redundant and wrong all at once. It says nothing to anyone who is not a mathematician - no, actually it says: "run away!". It is redundant because a Clifford algebra is /always/ a vector space with a quadratic form. And quadratic forms in general have nothing to do with GA, only quadratic spaces, and even then nothing is lost by just coming out and saying that in GA, the square of a vector is a real number - but it shouldn't be in the introduction. Finally it is wrong because it fails to identify the distinguishing characteristic of GA, that it has a geometric interpretation, and may give the impression that GA is restricted to representing real numbers.

A related quibble is the "definition and notation" section. No mention of why V=R^n, or the combinatorial building up of higher-dimensional subspaces using the outer product or how their grades follow the pattern of Pascal's triangle / binomial theorem. It is phrased clumsily so the naive reader might think that a signature containing a zero e.g. G(2,0), or with null vectors, doesn't have an orthonormal basis. The Cℓ(V,Q) notation is never seen in GA papers, aside from throat-clearing remarks, and then only by the most pedantic mathematicians. Cℓ(p,q) is often seen as a notation for the signature, though. A more abstruse complaint is that this section also implies that null vectors in the basis are independent of the + and - vectors - they aren't, G(p,q,o) can always be converted to G(p+1,q+1), or back the other way, and that is always done explicitly in practice whenever null vectors are introduced.

Null basis vectors, mixed-signature spaces, even negative signature spaces are not the place to start for a reader we must presume has never heard of any of these things before. Here's a rough sketch of the sort of sequence that I thing would have a much better chance of working: Start with G(2,0) with an orthonormal basis, explain the axioms with concrete examples, relate it to experience with plane geometry, get across the idea of a bivector and pseudoscalar, show how multiplying one of the basis vectors by it gives the other (dualization), relate to rotation and complex numbers, move to 3D to distinguish the pseudoscalar from bivectors, then the general pattern of Pascal's triangle and how its symmetry implies that each basis blade can be paired with a dual, apply to axial vectors / bivector duality, show why the whole R^n basis is needed for 4D (e12 + e34 is a bivector, but not a product of vectors). THEN get into other signatures, non-orthonormal frames, etc. (perhaps with a bit more on factoring, classification, Bott periodicity than is in the article now) The "rigorous" stuff can be left to near the end, or better yet, kept in the Clifford Algebra article, or relegated to references if it doesn't actually aid understanding for newcomers to the topic. Enon (talk) 08:56, 8 May 2013 (UTC)

I've just now added a further sentence to the lead in the hope that it makes the subject more approachable to laypersons, especially high-school students. I think that the remarkable fact that GA allows something that's entirely forbidden in linear algebra is something that high-school students would appreciate to know. It could open the readers' minds to the subject. Feel free to add/change/criticize. --Chris Howard (talk) 16:44, 7 May 2013 (UTC)

Nice start, thanks. M∧Ŝc²ħεИ_τlk 17:00, 7 May 2013 (UTC)

To Enon: it would be extremely helpful if you could be more concise (WP:TLDR), even by just listing all your proposed changes in bullet points. The above paragraph isn't very readable. Thanks, M∧Ŝc²ħεИ_τlk 09:14, 8 May 2013 (UTC)

Enon, I see where you are coming from, certainly I would agree that all the CA stuff can usefully be covered by reference to that article which is more directed at mathematicians than applied folk (like myself). The business about symbol manipulation is a bit of a red herring, the point is that GA allows far more (and more intuitive) symbol manipulation before you get to where you have to use coordinates in order to calculate something, then it's a question of whether there exists a good enough (ie on a par with those for vector algebra) implementation for those calculations. I would also prefer to see a specific list of amendments assuming that no-one is available to actually rewrite the entire article (you may add your preferred pdf's in the link list)Selfstudier (talk) 11:28, 8 May 2013 (UTC)

That gets at a little paradox I've noticed with GA. We would like it to "clarify and simplify" everything with geometric notions, but honestly you need quite a bit of exposure to vector algebra and other traditional ways of doing things to appreciate the simplification! Maybe we are just fooling ourselves... or maybe in the coming decades someone will polish GA until it shines as much as vector algebra in the past. Rschwieb (talk) 15:37, 8 May 2013 (UTC)

As an aside, GA is sort of an irony... You can't picture the "geometric" product except for the special cases of parallel or perpendicular vectors, which is annoying (IMO). Similarly for multivectors as a "scalar plus a vector plus a bivector"... Same with spinors... (topological analogies of "Möbius bands" (apparently wrong) or "books/belts" and the like are only partially helpful...) You just have to rely on vectors and take everything from there, in the intuition behind bivectors and higher grades... M∧Ŝc²ħεИ_τlk 15:49, 8 May 2013 (UTC)

Enon has a point about the first sentence of the lead. All it is trying to say is:

A geometric algebra is a Clifford algebra in which the underlying field is the real numbers.

Perhaps we should substitute this sentence? — Quondum 01:00, 9 May 2013 (UTC)

That's a little better, but it still will lead most people to think that GA can't deal with complex numbers, quaternions, etc. A more comprehensive rewrite of the intro would be better, something along the lines of:

"Geometric algebra applies Clifford algebra to geometric problems in physics and computation. Intuitively, Clifford algebra expands on the idea of vector spaces by using as its basis not just a set of n vectors to represent an n-dimensional space, but all the possible combinations of those vectors as well (using the "outer product", see below), thus creating a space of 2ⁿ degrees of freedom or "blades". The additional degrees of freedom are interpreted in geometric algebra as oriented areas, volumes, and higher-dimensional subspaces. Bivectors (the plane areas formed by combining pairs of vectors) in particular are frequently used, for instance to simplify and generalize the representation of rotations and to replace axial vectors in magnetism. A weighted sum of different blades can be constructed in a way similar to the separate real and imaginary parts of a complex number, but with up to 2ⁿ parts. Such a hypercomplex number is called a "multivector". Although the weighting coefficients in a multivector are real numbers, other fields including complex numbers and quaternions can be represented by certain types of multivectors.

The square of a vector in geometric algebra is always a real number, but as with imaginary numbers, the square may be negative. A wide range of spaces is representable using geometric algebra, including euclidean and non-euclidean spaces of any dimension. Euclidean spaces have basis vectors which all have the same sign when squared, while non-euclidean spaces such as those used in relativity have a mixed signature."

Now, this leaves all the precise definitions out, it sweeps a few things under the rug that have to be clarified in the rest of the article but it should be comprehensible to anybody who passed Algebra II in high school and it conveys as detailed an understanding of what I think are the most essential points as I can manage in a small space. It needs wikilinks and there are some other topics that should be mentioned in the intro as well, but care is needed to avoid allowing minor points to get in the way of clarity on the major points. Enon (talk) 18:46, 9 May 2013 (UTC)

And in reply to this last comment by Maschen: something that has bothered me for ages is that in application, most multivector objects in GA are restricted to subspaces: there are objects that are always scalar, always 1-vector, always 2-vector, always pseudoscalar, always a blade etc. (addressed in the lead, but not the body). The most complex objects in typical use for actually representing something that I'm aware of are rotors (or spinors). I've even seen it suggested that the addition operation should be eliminated (but I think this really applied to CGA specifically). That all the operations fit into a CA does not mean that the full space of a real CA is ever needed in a GA. It would be really nice if someone has ideas of how to address this aspect in the article. — Quondum 01:21, 9 May 2013 (UTC)

Nice sentence proposal, by all means substitute as you propose.

I've probably said this before, but that rotor diagram File:GA planar rotations.svg probably is as close as we can get to depicting the geometric product of vectors (but even then restricted to normalized vectors >_<).

Maybe we could create a talk:Geometric algebra/Sandbox for people to experiment in? I thought to just do it, link is at the top. M∧Ŝc²ħεИ_τlk 04:48, 9 May 2013 (UTC)

I've moved a copy draft of Enon's suggested rewrite to the page Maschen created. Let's work on it there. To avoid confusion, Enon, please bottompost your replies. Thanks! Rschwieb (talk) 21:19, 9 May 2013 (UTC)

OK, this discussion continues at talk:Geometric algebra/SandboxEnon (talk) 21:20, 10 May 2013 (UTC)

Suggestion for inner products

According to this article by Jaap Suter (IMO a very nice one), all the products can be expressed in terms of the others. Would it be possible to fill in a table like this? M∧Ŝc²ħεИ_τlk 11:05, 10 May 2013 (UTC)

Product...	...in terms of...
	$\wedge$	${\big \lrcorner }$	${\big \llcorner }$
$C\wedge D=$	$C\wedge D$	$(C\;{\big \lrcorner }\;(DI^{-1}))I$	$I((I^{-1}C)\;{\big \llcorner }\;D)$
$C\;{\big \lrcorner }\;D=$	$(C\wedge (DI^{-1}))I$	$C\;{\big \lrcorner }\;D$
$C\;{\big \llcorner }\;D=$	$I((I^{-1}C)\wedge D)$		$C\;{\big \llcorner }\;D$
$C*D=$	$((CD)\wedge I^{-1})I$
$C\bullet D=$
$\,C\bullet _{H}D=$

Wow, that's really interesting, and I plan to pursue it, but I'm not sure if it would be good to have in the article... Not dead-set against it though. Rschwieb (talk) 15:05, 10 May 2013 (UTC)

I don't agree with it being in the article, except maybe as a footnote. I missed Jaap Suter's mention of the relationship between the various products on a quick scan, but no matter. Any list of such interrelationships would have to include the wedge product: the wedge product and the two contractions can be expressed in terms of each other, just by multiplying appropriately by the psuedoscalar (alternatively using duals) in the right places. The others become a little more involved, requiring sums of products, e.g. the sum of the left and right contractions is the sum of the scalar and fat dot product, or something like that. I'd think that the former relationships have the most significance. — Quondum 01:06, 14 May 2013 (UTC)

I think it might be useful to many readers to have a reference section of basic definitions, common symbols, rules and equations including the sorts of stuff that was in the front and back inner cover pages of Dorst, Fontijne, and Mann's Geometric Algebra for Computer Science. Anything that can bring some more clear order to the proliferation of products is bound to be referred to frequently as well. Enon (talk) 22:01, 10 May 2013 (UTC)

We need to take care not to turn the article into a textbook or tutorial. Stuff of this nature should be put into a companion page if at all, named according to what it is acting as a reference for (much like lists of integrals etc.) — Quondum 01:06, 14 May 2013 (UTC)

... The whole point of this was an attempt to improve this article (GA) and I respectively disagree that it's "pedagogical/textbooky", what's wrong with presenting correlations? On the other hand I have been told I like tables too much and should desist from using them so much. In any case it's for take or leave. M∧Ŝc²ħεИ_τlk 17:49, 14 May 2013 (UTC)

Sorry, perhaps I was reading too much into the table approach in your outline approach. There may well be scope for showing a few relationships between the different multiplication operators under the section listing them. Hestenes's inner product does not fit algebraically with the others, but given a unit psuedoscalar $I$, one could put $(A\wedge B)I=A\;{\big \lrcorner }\;(BI)$ and $(A\;{\big \lrcorner }\;B)I=A\wedge (BI)$, and similar relations for the right contraction. This helps show that the operations are closely related. — Quondum 01:35, 15 May 2013 (UTC)

Don't get the wrong idea: I don't mind what format we use to present the correlations, a table just seemed natural. ^_^ Maybe just integrating lists into the prose would do. M∧Ŝc²ħεИ_τlk 07:05, 15 May 2013 (UTC)

The table would work if it had entries in nearly every location, and my first reaction was that it wouldn't, and that in some cases the entries would be quite complex expressions. It would probably work on this talk page while we're working out what we're talking about, so perhaps we should work on it here before I go jumping to conclusions about presentation. I've added some entries to the table. Could you give a page in Suter's article? — Quondum 11:20, 15 May 2013 (UTC)

p.24. M∧Ŝc²ħεИ_τlk 14:12, 15 May 2013 (UTC)

Thanks. Suter's wording does not imply that every product can be expressed in terms of any single one of the others. I think that they can all be expressed in terms of any single one of the first three, but these expressions are quite convoluted. Thus, the table should at least change by removing the last three columns, or allowing a freeform expression. For example, $C*D=C\;{\big \lrcorner }\;D+C\;{\big \llcorner }\;D-C\bullet D$. — Quondum 02:42, 16 May 2013 (UTC)

Degenerate GA claim

I removed the following (ignoring a little uncertainty in the one sign):

If a²=0 for every vector, then the geometric algebra is fully degenerate, and ab=0. To see this, we may write the geometric product of two vectors as the sum of two squares:

$ab={\frac {1}{4}}((a+b)^{2}-(a-b)^{2})$

Thus if every vector in the geometric algebra squares to zero, then the geometric product between any two vectors is also zero. Fully degenerate geometric algebras are therefore of limited interest. Assume there exist k linearly independent vectors $\{a_{1},...,a_{k}\}$ spanning a k-dimensional subspace of the overall n dimensional space such that $a_{1}^{2}\neq 0,...,a_{k}^{2}\neq 0$. If all the vectors of the remaining (n-k)-dimensional subspace square to zero, then the geometric product again acts trivially in that subspace. Hence it is enough to consider only the nondegenerate geometric algebra of k dimensions.

The claim that a²=0 ⇒ ab=0 is false; the premise merely leads to the results that ab=a∧b and a⋅b=0. Which is to say, a GA with a fully degenerate quadratic form is an exterior algebra, and not at all uninteresting. The further claim to the effect that null dimensions can be ignored is similarly invalid. This case is presented (with one degenerate dimension) in textbooks as the homogeneous case, and provides possibly the simplest algebra of geometric displacements (though the more powerful non-degenerate CGA would usually be preferred). A far more reasonable claim would be that every degenerate dimension can be replaced by two dimensions that square to the opposite sign (but I've not seen this in a reference). But that would belong elsewhere, not in the definition section. — Quondum 11:03, 29 May 2013 (UTC)

Come to think of it, why does this article not make the observation that when the quadratic form is fully degenerate, an exterior algebra results (as opposed to being contained in the GA)? I think that it used to do so long ago, or at least I've seen this in a reference somewhere. The construction of an exterior algebra from a tensor algebra is identical to that of a GA, except that the quadratic form is taken to be zero. — Quondum 11:19, 29 May 2013 (UTC)

Agreed. The exterior algebra is a really important case of a Clifford algebra. It was certainly not accurate to say they were of limited interest. And the problem with the equation you deleted was this: ${\frac {1}{4}}((a+b)^{2}-(a-b)^{2})=(2ab+2ba)/4$, but since a and b need not commute, it does not necessarily reduce to ab :) Rschwieb (talk) 13:48, 29 May 2013 (UTC)

Yes, and I jumped to a half-baked conclusion on my first edit. Second-guessing the how the equation was supposed to support the text is moot. Going off on a tangent: I wonder how useful my claim above (to the effect that every degenerate vector space can be embedded in a non-degenerate one, and thus correspondingly the GAs) would be? CGA does something like this, working with the degenerate (null) subspace of a non-degenerate GA. I suppose that this might belong in the CGA article. — Quondum 15:17, 29 May 2013 (UTC)

Yeah, sorry, I knew that looked a little strange. I think it's fixed now. Teply (talk) 16:05, 29 May 2013 (UTC)

Handling degeneracy in the form

Scribbling a little bit leads me to believe that a Clifford algebra over any symmetric form splits into A⊗B where A is an exterior algebra and B is the Clifford algebra of a subspace where the bilinear form is nondegenerate. We should look for a statement to this effect somewhere in the literature. Unfortunately, I don't have a feel for how this allows us to reduce to the case where we just study nondegenerate forms :) In a lot of other cases, things split up like this: A⊕B, and reduction is achieved by arguing that you can split your phenomenon to the pieces A and B, but with ⊗ things are not the same. (At least, I can't immediately see how to reduce.) Rschwieb (talk) 19:10, 29 May 2013 (UTC)

I think at least this is possible: If the bilinear form on V has kernel K, then when the bilinear form is passed down to V/K it becomes nondegerate. I guess I will have to do some thinking/digging to see how results on the quotient might pass back up to the original. Rschwieb (talk) 19:22, 29 May 2013 (UTC)

Oh, well this is neat. It says that the algebra for V/K is isomorphic to the algebra for V modulo its Jacobson radical. That is certainly interesting! In representation theory, you argue passing from R/rad(R) to R, so this is promising. Rschwieb (talk) 21:05, 29 May 2013 (UTC)

There are two reasons I was trying to downplay the degenerate geometric algebras with the new wording. The first reason is just that I wanted sharp contrast from the older wording. The wording I was replacing had the GA start with an orthonormal basis and the value Q(e)=+1,0,-1 for all the basis elements and their outer/inner products. That seems to me like putting the cart before the horse since the geometric product is what's defining this as a ring, and you'd normally only get to an orthonormal basis through the orthogonalization procedure I gave below. (You could also get there by the Gram–Schmidt process if it's all positive signature or if you happened to start with lucky, nonzero-norm guesses for your original basis vectors. Adding a brief section on that could be helpful.)

The second is that, well, degenerate geometric algebras aren't quite as "geometrical" like the spacetime algebra or other usual example. I was figuring most of the content on the degenerate ones could go into the more mathematical Clifford algebra article. The result you list above is fine and all. I think the intuition for it is that if you separate off the k basis vectors that span the nondegenerate subspace and the n-k vectors that span the degenerate subspace, all basis vectors of the entire space mutually orthogonal, then you can substitute the k basis vectors of the nondegenerate subspace with blades formed between them and the n-k degenerate ones. But it just seems like it would be really obscure to the non-mathemetician trying to read this general article as an introduction to the topic. Teply (talk) 23:20, 29 May 2013 (UTC)

I was mainly just mumbling to myself about degenerate spaces. I no intention of putting anything like that in the article (especially since I don't know any sources for it). I have a habit of treating this like a study group, and that's why I was saying we might look for the result :)

In any case, the two extremes (nondegenerate form and completely degenerate form) are prominent tools of geometry. Both have to be mentioned, but it would be fine to leave the completely degenerate case to exterior algebra and focus on nondegenerate signatures here, and downplay everything else.

I agree that the "start with orthonormal basis, define product on basis, extend to all of algebra" method is putting the cart before the horse, but realistically, that's how most texts on geometric algebra approach the construction. It has the benefit of being concrete. On the other hand, the "top down" method of defining it as a quotient of the tensor algebra is "the right direction," but it's inaccessible to non-mathematicians. Rschwieb (talk) 01:14, 30 May 2013 (UTC)

I'm simply focussing on correctness for now. Teply, I am pretty sure you are under a misapprehension in terms of being able to "ignore" the degenerate dimensions. It would be nice if we could simply define geometric algebras as dealing only with nondegenerate spaces, since this is mostly the case. However, I know of one case (with one degenerate dimension) that is treated within the field of GA, and that extra dimension has a purpose: it cannot be treated as an algebra with one less dimension (and the algebra has a decidedly geometric interpretation). AFAIK, the only sensible way of removing/separating degeneracy with a GA is to embed it in a non-degenerate GA that has additional dimensions – as many additional dimensions as the degeneracy of the original algebra. An approach you may prefer is to say that GA generally deals with nondegenerate vector spaces, but there is an exceptional case with one degenerate dimension (the homogeneous case) that is also sometimes studied. — Quondum 02:47, 30 May 2013 (UTC)

Sure, whatever. I'm just saying we shouldn't distract beginners with a "special topic" in the introductory sections. I view the goal of an overview article like this is to teach people "enough" so that they can explore the next degree of intermediate/advanced topics or specialization, e.g. geometric calculus, spacetime algebra, gimbal lock, efficient calculation of radiosity, gauge theory gravity, the classification of nondegenerate real Clifford algebras, or partially degenerate GA if it pleases the reader. Since to my knowledge those first several examples don't use degenerate GA, I guess I consider it to be a special topic. Either way, this article is clearly still needs a lot of attention. If you'd like to add a section on degenerate GA, or even a full-fledged article, I'm certainly not here to stop you. Teply (talk) 03:53, 30 May 2013 (UTC)

In my latest edits, I've tried to keep with the approach of minimizing distractions, and focussing on the non-degenerate cases. Hopefully what I've done will satisfy us both, since I've removed stuff that would only serve as a distraction. BTW, my claim that the homogeneous model necessarily uses a degenerate algebra was not supported by one reference I checked (Dorst, I think it was): they prefer a nondegenerate algebra even then. — Quondum 14:05, 30 May 2013 (UTC)