Talk:Superior highly composite number

The same as colossally abundant numbers?

Aren't these the same thing as Colossally abundant numbers???? The articles should be combined if so.Scythe33 14:35, 14 Jun 2005 (UTC)

I'm not an expert, but it appears they are different. In the definition of superior highly composite number, the exponent is required to be > 0, whereas in the definition of colossally abundant number, the exponent is required to be > 1, so every colossally abundant number is superior highly composite, but not conversely. See also the links to the encyclopedia of integer sequences. Revolver 6 July 2005 18:32 (UTC)

They're two completely different things. Superior highly composite numbers are defined in terms of number of divisors (d function); colossally abundant numbers are defined in terms of sum of divisors (sigma function). DPJ, 16 Aug 2005 6:13 UTC

According to OEIS data the first 15 numbers of both series are the same. — Preceding unsigned comment added by 2.39.181.209 (talk)

Yes, and then they have differences with both sequences containing numbers not in the other. PrimeHunter (talk) 23:44, 16 February 2013 (UTC)

Further research shows that the definition is wrong. (At 14:27, 14 June 2005 Scythe33 changed the definition; the article was right the first time.) According to the definition supplied by Scythe33, every highly composite number would qualify. DPJ, 16 Aug 2005 6:21 UTC

Why isn't n=1 included as a superior highly composite number? Putting $\epsilon$ = 1, we get $d(k)/k\leq 1=d(1)/1$, which suggests that 1 is a superior highly composite number. DRLB 14:56, 19 October 2006 (UTC)

Umm...

Wow, this is densely packed information. There's a formal definition given, which I'm sure is easy to understand for mathematicians, but I'm no slouch at math myself and it's clear as mud to me. Can someone give an informal definition? Matt Yeager ♫ (Talk?) 22:55, 20 May 2008 (UTC)

I cannot think of a good less formal definition. An example might be better (not formatted properly for article space). Consider ε=0.6. Rounded to 3 decimals, the value of d(k)/k^0.6 for k = 1, 2, ... is 1.000, 1.320, 1.035, 1.306, 0.761, 1.365, 0.622, 1.149, 0.803, 1.005, ... It can be proved (skipped here) that the value for k=6, d(6)/6^0.6 = 1.365, is the largest value in this infinite sequence. Therefore 6 is a superior highly composite number. The same value of ε can never be used for two distinct superior highly composite numbers, since at most one of them can give the maximal value of d(k)/k^ε. Does this help? PrimeHunter (talk) 00:20, 21 May 2008 (UTC)

On second thought, there may be boundary values of ε where distinct superior highly composite numbers give the same maximal value of d(k)/k^ε. PrimeHunter (talk) 00:26, 21 May 2008 (UTC)

I think I get it. So... if I take a positive integer, and divide its # of divisors by the original number raised to the power of ε (which is just any positive number), and the result I get is the maximum for that function, than the positive integer I used must be a superior highly composite number. If I'm right, than you have explained this very well (and I realize it's really difficult to give any less formal of a definition than what the article states... thank you very much!). Matt Yeager ♫ (Talk?) 09:49, 24 May 2008 (UTC)

You are right. I will add a better formatted example to the article later. PrimeHunter (talk) 12:36, 24 May 2008 (UTC)

I still don't get it although I am supposed to be a mathematician, epsilon-(delta) never was my forte though. --84.208.152.226 (talk) 18:45, 6 November 2010 (UTC)

I feel your pain. A while ago I added in the first sentence that it was a more restrictive definition of "compositeness" than a highly-composite number (the definition of which is way easier to understand).

My goal was for the first sentence to get the basic idea down in English, with the lack of an illustrative mathematical explanation beyond the following formula to serve as a warning, but I think it can be further improved by saying "Know ye who read past the lead, this definition eludes intuitive analysis, so if thou seeketh compositeness, verify that highly composite number be not sufficient." SamuelRiv (talk) 17:48, 30 July 2014 (UTC)

Is 840 an example?

There has been controversy over whether 840 should be included in the list: 164.127.191.68 (talk · contribs · WHOIS) asserts that it should. However, (sequence A002201 in the OEIS) disagrees. Deltahedron (talk) 18:23, 11 July 2014 (UTC)

Sorry, but i don,t understand the definition of highly composite numners. 94.254.209.29 (talk) 20:12, 25 July 2014 (UTC)

I don't see the controversy, since a counterexample range in which to search is easy to find and quick to search to very high numbers, though those will still diverge. The easiest way to check counterexamples, is only to compare the two existing SHC numbers above and below 840, and see (using plotting software like Mathematica) if there's any epsilon range for which they both satisfy the inequality. My Mma code, factoring out 840^eps, was this:

Plot[{32 - 24*(7/3)^eps, 32 - 48*(1/3)^eps}, {eps, .2, 1}]

The nearest they got to both being positive was at eps=.355. Of course, a plot isn't necessary, since you can quickly check thousands of possibilities by either looking only in the range of epsilons at which consecutive SHC#'s are valid and manually checking anything that misses the inequality, or compare the intersection and slopes of two curves in epsilon to find where they peak. Many ways to do it.

tldr; no, 840 is provably not a SHC number. SamuelRiv (talk) 19:06, 30 July 2014 (UTC)

Definition?

This:

    In mathematics, a superior highly composite number is a natural number which has more divisors than any other number scaled relative to the number itself

should be defined. Wlod (talk) 07:01, 22 October 2014 (UTC)

It was originally a lose description after the definition [1] but then the lead was restructured so it sounded like the definition itself while the actual definition sounded like a derived property. I don't have time to improve it now. PrimeHunter (talk) 12:36, 22 October 2014 (UTC)

Factors of the first seventeen SHCNs

I obviously did not work this out by hand. :-) I did this for putting in the article, but they quickly became walls of text so enormous that I truncated it at the tenth SHCN (720720) – which already has every integer from 1 to 16 as a divisor!

see: /Factors

A neat illustration of just how superior highly composite these numbers are, I guess, but an impenetrable wall of text for the last few. Double sharp (talk) 14:44, 26 February 2015 (UTC)

The need to normalize the graphs

Divisor function d(n) up to n = 250

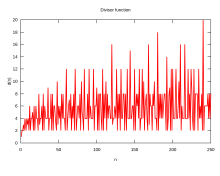
This graph:


...and the graph below it: File:Highly_composite_numbers.svg
both present good information. But this isn't the best info to present in order to communicate how highly composite a number is. One of the most important math concepts when analyzing data is normalization. For example, we don't say that China is a much more highly composite country than, say, Luxembourg. You expect there to be a much wider range of diversity of people within a country of more than a billion people than you would with a small country. So the important info jumps forward when you normalize the stats. How diverse is the population with respect to the size of the population? This is why you see "per capita" used so often. If you fail to normalize your data, important aspects within your dataset can get buried. Ok, now back to the topic of this article...

The key info to present in the graph is not merely how many divisors are within any number. You obviously expect there to be more divisors for larger numbers. So to capture the actual composite quality of any number, it must be normalized to the size of the number. One normalization method is to do a straight division of the number of divisors by the integer. But more meaningful info comes forward when the # of divisors is normalized by the method of dividing by the square of the integer. And a strong argument says that the proper normalization method is to divide the # of divisors by the cube of the integer. The argument for normalizing with a higher power of the integer is that divisors are not used to form a one-dimensional entity. A divisor need to be multiplied by something else in order to get back to the integer, so it can be considered to be an area or a volume-type of parameter (analogous to area/volume). And so the proper normalization is by dividing by the square or the cube of the integer.

When these graphs are properly normalized, then the special status of the numbers 12 and 60 become evident. But as the graphs stand today, all it really communicates is that "there are more people in China". Yes, it does an adequate job of showing that 360 is a special number. But these graphs have buried the reality of how much more special the composite qualities of 12 and 60 are. -- Tdadamemd19 (talk) 14:54, 5 April 2019 (UTC)

Well, that is the whole point of superior highly composite numbers: you have that n^−ε factor in the formula that scales the divisor function by some power of the number. Depending on what power you use, any of the superior highly composite numbers can have its turn at being the maximum; 2, 6, 12, 60, 120, 360, 2520, and so on. Double sharp (talk) 15:00, 5 April 2019 (UTC)

Yes. And the problem being highlighted is that the graphs do not show this.-- Tdadamemd19 (talk) 15:12, 5 April 2019 (UTC)

Here is another way to understand the need for proper normalization...

Consider the graph in the thumbnail above. Say that the x-axis and y-axis are scaled one-to-one. Then you can picture that there is an envelope ramping up and to the right from the origin at a 45-degree angle, representing the theoretical very best you can do with the magnitude of the number of divisors. So one proper normalization technique would be to scale the number of divisors as the percentage up to this theoretical maximum.-- Tdadamemd19 (talk) 15:18, 5 April 2019 (UTC)

Superior highly composite number or Convergence Point

I tweaked the opening statement... In mathematics, a superior highly composite number or convergence point is a natural number which has more divisors than any other number scaled relative to some positive power of the number itself. It is a stronger restriction than that of a highly composite number, which is defined as having more divisors than any smaller positive integer. 50.245.89.150 (talk) 01:38, 18 July 2019 (UTC)

Wording of the beginning sentence

I believe it needs to be reworded in a way that's more intuitive than how it is now. I made the (now reverted) change because I believed "when adjusted for magnitude" seemed much easier to understand than "scaled relative to some positive power of the number itself". For example, when I first read this, I thought "the number itself" was referring to the natural number in question, not just "any" number scaled relative to the same power of "any" number. What about a middle ground between my change and how it is now? Avengingbandit 20:14, 18 August 2021 (UTC)

@Avengingbandit: Now it gives the definition in words although it may be hard to understand and require some interpretation. "adjusted for magnitude" is not a definition without saying how the adjustment is made, which is impossible to guess in this case where the adjustment method is complicated and invented specificially for these numbers. Apart from being vague, I also think "adjusted for magnitude" is misleading because it would normally mean the same adjustment is made for all superior highly composite numbers. If that was the case then there could only be one number with more divisors than any other number "adjusted for magnitude". If we don't want a complicated definition and cannot make a simple definition then we shouldn't give something which sounds like a definition but isn't, and is misleading. How about: "a superior highly composite number is a natural number which has more divisors than any other number when adjusted for magnitude in a certain way which is a little different for each superior highly composite number." It may sound vague and clunky but it's correct. "in a certain way" makes it clear that this is not the actual definition, and "a little different for each superior highly composite number" explains how there could be more than one with more divisors than any other number. Without this part, many readers will probably think there must be an error in the sentence, e.g. that it should have said "more divisors than any smaller number". PrimeHunter (talk) 01:27, 19 August 2021 (UTC)

@PrimeHunter: The way you worded it makes it hard for me to tell if you're seriously suggesting "in a certain way which is a little different" wording; I would not be opposed to that if you are. Another suggestion of mine would be "more divisors than any other number when divided by some positive power of itself"? Replaces "scaled" with "divided" and "the number itself" with just "itself". You may not find that necessary but as a fellow reader I'd like to be able to clearly and unambiguously understand what I'm reading. I wouldn't see anything wrong with that. Avengingbandit 02:12, 19 August 2021 (UTC)

@Avengingbandit: That sounds good. PrimeHunter (talk) 01:28, 20 August 2021 (UTC)

@L 106.79.204.198 (talk) 22:33, 25 February 2024 (UTC)