Talk:Vector projection
| This article is rated B-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
Using lowercase letter for scalar projection[edit]
Using a lowercase letter for scalar projection is quite common. I added a new section Vector projection#Notation in which I explained this notation. See also this text copied from Euclidean vector:
From Euclidean vector Another way to represent a vector in n-dimensions is to introduce the standard basis vectors. For instance, in three dimensions, there are three of them: These have the intuitive interpretation as vectors of unit length pointing up the x, y, and z axis of a Cartesian coordinate system, respectively. In terms of these, any vector a in can be expressed in the form:
where a1, a2, a3 are called the vector components (or vector projections) of a on the basis vectors or, equivalently, on the corresponding Cartesian axes x, y, and z (see figure), while a1, a2, a3 are the respective scalar components (or scalar projections).
In introductory physics textbooks, the standard basis vectors are often instead denoted (or , in which the hat symbol ^ typically denotes unit vectors). In this case, the scalar and vector components are denoted respectively ax, ay, az, and ax, ay, az (note the difference in boldface). Thus,
Paolo.dL (talk) 16:09, 24 April 2013 (UTC)
- My problem with this notation is the text sometimes refers to a1. Is that the vector or the scalar? For the sake of readers completely unfamiliar with the subject, we should really improve notation so we aren't calling two different things by nearly the same name, because that's confusing.. many readers might not realise that bolding is significant. There's no harm is using an unambiguous name (it's not like there are widely accepted standards here anyway, since there are so many different possible contexts). Mark M (talk) 17:38, 24 April 2013 (UTC)
- I added a new section Vector projection#Notation in which I explained this notation. People commonly uses it. Why should the readers be treated as dumb people? It is useful for them to learn this notation.
- Similarly, it is confusing to use c or s for the scalar component of a. How do you call then the scalar component of a vector c or s? Every vector has its own components:
- By the way, I disagree that the text uses a1 without calling it explicitly scalar projection and/or offering an evident comparison with the symbol used for vector projection.
- In short, I don't think that this is confusing, I think it is useful and important to know.
- Paolo.dL (talk) 10:30, 26 April 2013 (UTC)
Proposed merge[edit]
Essentially all of the content in Scalar projection is already in this article, so there's no need to have duplicate information. So a merge makes sense to me. Mark M (talk) 17:38, 24 April 2013 (UTC)
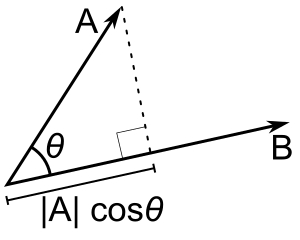
- Not all of the content in Scalar projection is already in this article.
- Anyway, my point is that Scalar projection is shorter and more focused than Vector projection. Hence it is useful for those who only seek to learn what a scalar projection is. This is desirable, as the concept of scalar projection is quite commonly and frequently used, for instance to explain Cartesian coordinates and Euclidean vector components, see above.
- Notice that the scalar projection is not defined, in the separate article scalar projection, in terms of vector projection (see figure, taken from the introdution of Scalar projection). It is defined as
- It coincides with the magnitude of the vector projection only when 0° ≤ θ ≤ 90°. So, the concept of scalar projection can be easily understood without learning about vector projection.
- Vector projection also includes info about vector rejection, and a lot of info which is not really needed for those who just want to understand how a scalar component of a vector is defined. Most readers do not need to know what a vector rejection is...
- Paolo.dL (talk) 10:20, 26 April 2013 (UTC)
- Obviously all articles are supposed to be as focused, concise, and to the point as possible. All the points you think do not overlap, or are not defined, can still be easily collectively explained in one article. The same article would make any similarities/differences clearer. M∧Ŝc2ħεИτlk 21:04, 26 April 2013 (UTC)
- You already have an article where the similarities/differences between scalar projection, vector projection and vector rejection are made clear. But this comparison is useless for many readers, interested only in the scalar projection. A separate article concerning only the scalar projection is needed, because:
- it has a much smaller scope (it does not need to explain in detail vector projection and rejection)
- it makes perfectly sense (it is not incomplete)
- it is likely to be enough for many readers, who don't care about vector projection and rejection.
- Paolo.dL (talk) 23:57, 26 April 2013 (UTC)
- You already have an article where the similarities/differences between scalar projection, vector projection and vector rejection are made clear. But this comparison is useless for many readers, interested only in the scalar projection. A separate article concerning only the scalar projection is needed, because:
Performance info[edit]
I removed an erroneous note about performance (https://en.wikipedia.org/w/index.php?title=Vector_projection&type=revision&diff=857678811&oldid=800732724). The note claimed the latter method was faster, when in reality it depends on the platform, implementation, and context (but the former is probably faster). The normalization is likely to boil down to multiplication by a reciprocal square root, which is quite fast on modern CPUs. However, counting operations is not a very good way to reason about performance, so even that doesn't tell the whole story. If anyone wants to add performance-related information back into the article, please make sure are aware of all the relevant details first, to avoid giving bad advice. 72.161.48.132 (talk) 09:09, 2 September 2018 (UTC)
Remove hat notation[edit]
I was unfamiliar with the hat notation for normalized vectors. To me, hats are more commonly used for estimated values (e.g. mean quantities, statistical estimators, or best-fit parameters). While I acknowledge that using hats are used for normalized vectors in some fields/articles, I feel like for this article it is unnecessary. I propose that be replaced with . It won't complicate the equations much, and then we can remove the two places where the hat notation is described. --Quantum7 09:04, 9 May 2019 (UTC)
Proposed merge of Scalar projection into Vector projection[edit]
wide overlap; possibly renaming to Vector and scalar projection. fgnievinski (talk) 05:35, 4 September 2023 (UTC)
- Oppose Not a good idea. 2001:8003:9100:2C01:CCD4:1B3:1477:E53 (talk) 00:46, 3 February 2024 (UTC)













