Transmission loss (duct acoustics)
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
| Sound measurements | |
|---|---|
Characteristic | Symbols |
| Sound pressure | p, SPL, LPA |
| Particle velocity | v, SVL |
| Particle displacement | δ |
| Sound intensity | I, SIL |
| Sound power | P, SWL, LWA |
| Sound energy | W |
| Sound energy density | w |
| Sound exposure | E, SEL |
| Acoustic impedance | Z |
| Audio frequency | AF |
| Transmission loss | TL |
Transmission loss (TL) in duct acoustics describes the acoustic performances of a muffler-like system. It is frequently used in the industry areas such as muffler manufacturers and NVH (noise, vibration and harshness) department of automobile manufacturers, and in academic studies. Generally the higher transmission loss of a system it has, the better it will perform in terms of noise cancellation.
Introduction
[edit]Transmission loss (TL) in duct acoustics is defined as the difference between the power incident on a duct acoustic device (muffler) and that transmitted downstream into an anechoic termination. Transmission loss is independent of the source,[1][2] if only plane waves are incident at the inlet of the device.[2] Transmission loss does not involve the radiation impedance inasmuch as it represents the difference between incident acoustic energy and that transmitted into an anechoic environment. Being made independent of the terminations, TL finds favor with researchers who are sometimes interested in finding the acoustic transmission behavior of an element or a set of elements in isolation of the terminations. But measurement of the incident wave in a standing wave acoustic field requires uses of impedance tube technology, may be quite laborious, unless one makes use of the two-microphone method with modern instrumentation.[1][2]
Mathematical definition
[edit]
By definition the plane wave TL on an acoustic component with negligible mean flow may be described as:[1]
where:
- is the incident sound power in the inlet coming towards muffler;
- is the transmitted sound power going downstream in the outlet out of the muffler;
- stand for the cross-sectional area of the inlet and outlet of muffler;
- is the acoustic pressure of the incident wave in the inlet, towards muffler;
- is the acoustic pressure of the transmitted wave in the outlet, away from muffler.
- is the particle velocity of the incident wave in the inlet, towards muffler;
- is the particle velocity of the transmitted wave in the outlet, away from muffler.
Note that cannot be measured directly in isolation from the reflected wave pressure (in the inlet, away from muffler). One has to resort to impedance tube technology or two-microphone method with modern instrumentation.[1] However at the downstream side of the muffler, in view of the anechoic termination, which ensures .
And in most muffler applications, Si and So, the area of the exhaust pipe and tail pipe, are generally made equal, thus we have:
Thus, TL equals 20 times the logarithm (to the base 10) of the ratio of the acoustic pressure associated with the incident wave (in the exhaust pipe) and that of the transmitted wave (in the tail pipe), with the two pipes having the same cross-sectional area and the tail pipe terminating anechoically.[1] However this anechoic condition is normally difficult to meet under practical industry environment, thus it is usually more convenient for the muffler manufacturers to measure insertions loss during their muffler performance tests under working conditions (mounted on an engine). However, there is no relationship between the insertion loss and the transmission loss of a muffler.
Also, since the transmitted sound power cannot possibly exceed the incident sound power (or is always larger than ), it is known that TL will never be less than 0 dB.
If the system contains non-negligible mean flow and have duct sizes which support wave modes of orders higher than the plane wave mode at the frequencies of interest, transmission loss calculations are modified accordingly.[2]
Transmission matrix description

The low-frequency approximation implies that each subsystem is an acoustic two-port (or four-pole system) with two (and only two) unknown parameters, the complex amplitudes of two interfering waves travelling in opposite directions. Such a system can be described by its transmission matrix (or four-pole matrix), as follows[3]
- ,
where ,, and are the sound pressures and volume velocities at the input and at the output. A, B, C and D are complex numbers. With this representation it can be proved that the transmission loss (TL) of this subsystem can be calculated as,
- ,
where:
- is inlet and outlet cross-sectional area;
- are media density and sound velocity.
A simple example
[edit]
Considering we have the most simplest reactive silencer with only one expansion chamber (length l and cross-sectional area S2), with inlet and outlet both having cross-sectional area S1). As we know the transmission matrix of a tube (in this case, the expansion chamber) is[3]
- .
Substitute to the equation of TL above, it can be seen that the TL of this simple reactive silencer is
where is the ratio of the cross-sectional areas and is the length of the chamber. is the wave number while is the sound speed. Note that the transmission loss is zero when is a multiple of half a wavelength.
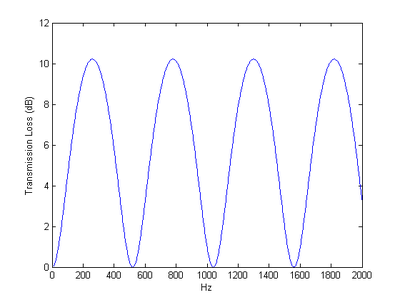
As a simple example, consider a one chamber silencer with h=S1/S2=1/3, at around 400 °C the sound speed is about 520 m/s, with l=0.5 m, one easily calculate the TL result shown on the plot on the right. Note that the TL equals zero when frequency is a multiple of and TL peaks when frequency is .
Also note that the above calculation is only valid for low-frequency range because at low-frequency range the sound wave can be treated as a plane wave. The TL calculation will start losing its accuracy when the frequency goes above the cutoff frequency, which can be calculated as ,[1] where D is diameter of the largest pipe in the structure. In the case above, if for example the muffler body has a diameter of 300mm, then the cut-off frequency is then 1.84*520/pi/0.3=1015 Hz.
References
[edit]- ^ a b c d e f Munjal, M.L. (1987). Acoustics of ducts and mufflers with application to exhaust and ventilation system design. New York: Wiley. pp. 58–60. ISBN 0471847380.
- ^ a b c d Dokumaci, Erkan (2021). Duct Acoustics: Fundamentals and Applications to Mufflers and Silencers. Cambridge University Press. pp. 177, 492, 512. ISBN 978-1-108-84075-0.
- ^ a b Jacobsen, Finn (2000). Propagation of sound waves in ducts - DTU. Technical University of Denmark. p. 68.































