User:Markozeta/sandbox
Appearance
Area moments of inertia
[edit]| Description | Figure | Area moment of inertia | Comment | Reference |
|---|---|---|---|---|
| a filled circular area of radius r |  |
[1] | ||
| an annulus of inner radius r1 and outer radius r2 | 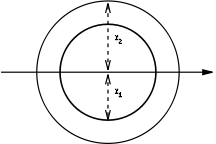 |
For thin tubes, and .
We can say that and because this bracket can be simplified to . Ultimately, for a thin tube, . |
||
| a filled circular sector of angle θ in radians and radius r with respect to an axis through the centroid of the sector and the center of the circle |  |
This formula is valid for only for 0 ≤ ≤ | ||
| a filled semicircle with radius r with respect to a horizontal line passing through the centroid of the area |  |
[2] | ||
| a filled semicircle as above but with respect to an axis collinear with the base |  |
This is a consequence of the parallel axis theorem and the fact that the distance between these two axes is | [2] | |
| a filled semicircle as above but with respect to a vertical axis through the centroid |  |
[2] | ||
| a filled quarter circle with radius r entirely in the 1st quadrant of the Cartesian coordinate system |  |
[3] | ||
| a filled quarter circle as above but with respect to a horizontal or vertical axis through the centroid |  |
This is a consequence of the parallel axis theorem and the fact that the distance between these two axes is | [3] | |
| a filled ellipse whose radius along the x-axis is a and whose radius along the y-axis is b |  | |||
| a filled rectangular area with a base width of b and height h |  |
[4] | ||
| a filled rectangular area as above but with respect to an axis collinear with the base |  |
This is a result from the parallel axis theorem | [4] | |
| a filled rectangular area as above but with respect to an axis collinear, where r is the perpendicular distance from the centroid of the rectangle to the axis of interest | This is a result from the parallel axis theorem | [4] | ||
| a filled triangular area with a base width of b and height h with respect to an axis through the centroid |  |
[5] | ||
| a filled triangular area as above but with respect to an axis collinear with the base |  |
This is a consequence of the parallel axis theorem | [5] | |
| a filled regular hexagon with a side length of a |  |
The result is valid for both a horizontal and a vertical axis through the centroid, and therefore is also valid for an axis with arbitrary direction that passes through the origin. | ||
| An equal legged angle |  |
is the often unused product of inertia, used to define inertia with a rotated axis | ||
| Any plane region with a known area moment of inertia for a parallel axis. (Main Article parallel axis theorem) |  |
This can be used to determine the second moment of area of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's center of mass and the perpendicular distance (r) between the axes. |
- ^ "Circle". eFunda. Retrieved 2006-12-30.
- ^ a b c "Circular Half". eFunda. Retrieved 2006-12-30.
- ^ a b "Quarter Circle". eFunda. Retrieved 2006-12-30.
- ^ a b c "Rectangular area". eFunda. Retrieved 2006-12-30.
- ^ a b "Triangular area". eFunda. Retrieved 2006-12-30.





































