Talk:Vertex figure/polychoron
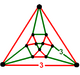
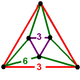
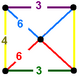
Vertex figures (as Schlegel diagrams) for Uniform polychora, Uniform honeycombs (Euclidean and hyperbolic). (Excluding prismatic forms)
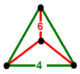
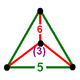
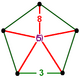
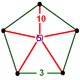
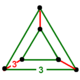
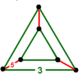
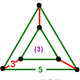
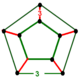
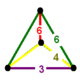
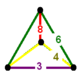
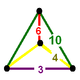
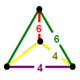
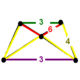
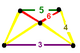
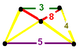
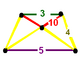
NOTE: Each vertex figure edge represents a face in the polytope and is labeled and colored by its side count of that face. Edges are also colored by symmetry so the same polytope can have different colors based on different generator groups. In general every pair of mirrors can generate a different face, so a 4-mirror generator can have 6 types of faces. The Coxeter-Dynkin diagram shows lines excluding order 2 mirror (node) pairs, but those pairs can generate square faces when both are active. Such faces are always labeled yellow. Others are generally colored red, green, and purple for the p,q,r order elements. (That's the plan, in actuality, my diagrams are not completely colored this way, some due to repeating with p and r colors flipped for being the same.)
Tom Ruen (talk) 04:30, 27 August 2009 (UTC)
Vertex figures
[edit]Using the vertex figure diagrams for the uniform 4-polytopes in Conway's new book, I made some crude diagrams for vertex figures for the cubic honeycomb family. I think they're simpler than the 3D diagrams which don't have edges labeled by face order. I colored them based on {p,q,r}, with red={p}, green={q}, purple={r}, yellow={}x{}={4}
I'll have to think a bit more what a coloring means for the bifurcating D4 family! (and prismatic forms as well.)
I made the same for the Talk:Convex_uniform_honeycomb#Vertex_figures. If this is good, perhaps someone with SVG skills can make some nicer ones!
Tom Ruen (talk) 00:35, 12 December 2008 (UTC)
P.S. One thing Conway's book does that I don't is use double-lines for the x2 multiplied forms. Tom Ruen (talk) 01:16, 12 December 2008 (UTC)
Linear groups
[edit]Summary:
Vertex figures for uniform polychorons and honeycombs, generated from 8 families {p,q,r}, 5 being self-dual.
| Family | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| {p,3,3} | {3,p,3} | {p,3,4} | {p,3,5} | ||||||||||||
| Spherical | Spherical | Spherical | Spherical | Hyperbolic | Spherical | Euclidean | Hyperbolic | Spherical | Hyperbolic | Hyperbolic | |||||
| Forms | {p,q,r} | {3,3,3} | {4,3,3} | {5,3,3} | {3,4,3} | {3,5,3} | {3,3,4} | {4,3,4} | {5,3,4} | {3,3,5} | {4,3,5} | {5,3,5} | |||
| Regular |
{q,r} |  {3,3} |
 {3,3} |
 {3,3} |
 {4,3} |
 {5,3} |
 {3,4} |
 {3,4} |
 {3,4} |
 {3,5} |
 {3,5} |
 {3,5} | |||
| Truncated |

|

|

|

|
|
|

|

|

|

|
|
| |||
| Rectified |

|
|

|
|

|
|

|

|

|
|
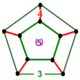
|

| |||
| Bitruncated |

|

|

|

|

|
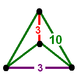
|

|

|

|

|

|
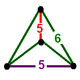
| |||
| Cantellated |

|

|

|

|

|
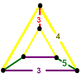
|

|

|

|
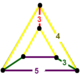
|

|
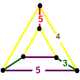
| |||
| Runcinated |

|

|

|

|

|
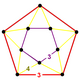
|

|
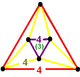
|

|

|

|

| |||
| Cantitruncated |

|
|
|

|

|
|
|
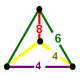
|

|
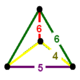
|
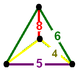
|
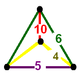
| |||
| Runcitruncated |

|
|

|

|

|
|

|

|

|

|
|
| |||
| Omnitruncated |

|

|

|

|

|

|

|
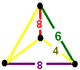
|

|

|

|

| |||
Loop and tail
[edit]| Hyperbolic | ||||
|---|---|---|---|---|
| Coxeter-Dynkin diagram |
||||
Bifurcating
[edit]| # | Space | Spherical | Euclidean | Hyperbolic | |
|---|---|---|---|---|---|
| Coxeter-Dynkin diagram |
p=3 | p=4 | p=5 | p=6 | |
| 1 | 
|

|

| ||
| 2 | 
|
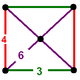
|

| ||
| 3 | 
|
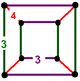
|

| ||
| 4 | 
|

|

| ||
| 5 | 
|

| |||
| 6 | 
|

| |||
| 7 | 
|

|

| ||
| 8 | 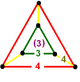
|
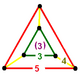
| |||
| 9 | 
|

|

| ||
| 10 | 
|
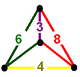
|
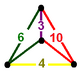
| ||
| 11 | 
|

|
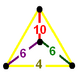
| ||
Cyclic [(p,q,r,s)]
[edit]| Space | Euclidean | Compact hyperbolic | Paracompact hyperbolic | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p,q,r,s | 3,3,3,3 | 4,3,4,3 | 5,3,5,3 | 4,3,3,3 | 5,3,3,3 | 5,3,4,3 | 6,3,3,3 | 6,3,4,3 | 6,3,5,3 | 6,3,6,3 | 4,4,3,3 | 4,4,4,3 | 4,4,4,4 |
| Coxeter-Dynkin diagram |
[(3,3,3,3)] |
[(4,3,4,3)] |
[(5,3,5,3)] |
[(4,3,3,3)] |
[(5,3,3,3)] |
[(5,3,4,3)] |
[(6,3,3,3] |
[(6,3,4,3)] |
[(6,3,5,3)] |
[(6,3,6,3)] |
[(4,4,3,3)] |
[(4,4,4,3)] |
[(4,4,4,4)] |
|

|

|

|

|

| ||||||||

|

|

| |||||||||||

|

|

|

|

| |||||||||
|

|

|

|

|

| ||||||||

|

|

| |||||||||||

|

|

|

|

|

| ||||||||
|

|

|

|

|

| ||||||||

|

|

| |||||||||||
 |

|

|

|

|

| ||||||||
References
[edit]- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 21, pp 292-298: Architechtonic and Catoptric 3-tessellation, Chapter 26: pp 389-403: Four dimensional Archimedean polytopes)



