Soil dryness index

Introduction

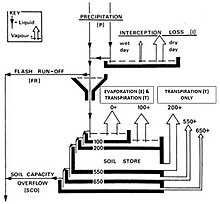
The Soil Dryness Index (SDI) is used to estimate the relative dryness of soil across tens of square kilometers with the simple inputs of daily rainfall and daily maximum temperature. The wetting and drying water budget approach (Figure 1) includes terms for precipitation (P), canopy interception loss (I), flash runoff (FR), Soil Capacity Overflow (SCO), evaporation (E) and plant transpiration (T). Most soils store water and the Index represents dryness in terms of millimeters of rainfall needed to fill the soil store with moisture to field capacity, that is, to nearly overflowing (see Figure 2). Each 1 mm of rain wets about 6 mm of soil from the top down so an SDI of 25 mm means that 25 mm of rain is needed to fill the last 150 mm of the soil store to almost overflowing.

Figure 2. The Soil Dryness Index(SDI) and drying then wetting of a generic soil profile in response to rainfall events (Mount 1972). Note the soil depth is in feet and rainfall and SDI is in points (4 pts = ~1 mm).

Soil dryness affects the dryness of fallen dead leaves, twigs, branches and trunks and other organic matter on the soil – all of which can be bushfire fuel when dry enough. Dry soils reduce live plant transpiration and growth. Very dry soils make live leaves wilt and let the sun in to dry out the soil under dense forest. The extreme dryness of those soils can cause drought deaths. On the other hand, heavy rain on wet soils can overfill the soil store and cause flooding. Fire management and flood and fire weather forecasting all require reliable measures of soil dryness.

Creating the Soil Dryness Index

To estimate soil dryness a 1966 preprint (McArthur 1966?) of the Keetch-Byram Drought Index (KBDI 1968) developed in North Carolina, USA was applied in mainland Australia but was found to give misleading results in cooler, temperate Tasmania. The Tasmanian Forestry Commission decided to adapt the KBDI to local conditions and the result was called the Soil Dryness Index (SDI) (Mount 1972, 1980). The best available data to make this adaptation were two years of daily measurement of weather, canopy interception (I), runoff and soil moisture on a set of small river catchments at Lidsdale, New South Wales (Bell and Gatenby 1969).

This data showed some runoff, that is flash runoff (FR), occurred even when rains fell on mostly dry catchments and that the drying of the soil was at five different rates. The refinement of the Keetch-Byram Drought Index for Tasmanian conditions drew on this data and that available from the Emu River catchment, Tasmania and required attention to both the soil wetting and the soil drying stages.

Flash runoff

A key refinement was to introduce a term into the model for flash runoff (FR), which is the rainfall that bypasses the soil because it falls directly on streams, lakes and connected waterlogged soils. It can be a significant quantity, for example, it made up 15% of the Emu River runoff though only 2% of the Lidsdale runoff.

Forest canopy interception and evaporation of rainfall

Forest canopy interception (I) of rainfall is an important term in estimating soil dryness. Forest canopy interception (I) reduces the rain reaching forest soils – so they get less than the rain gauge measures in its clearing. For a growing tree seedling, interception is zero below rain gauge height. Interception increases with canopy height and density.

In practice, there is a difference between the SDI and the KBDI methods, especially in lower rainfall areas. The KDBI method simply deducts 20 points (5 mm) of canopy interception from each rain period for all types of forest. The SDI refined the method by introducing seven classes of vegetation density to produce an improved estimate of the canopy interception and evaporation of rain from the canopy. In short, the SDI deducts more canopy interception from the rain gauge observation for denser forests plus some for every following wet day.

In more detail, the SDI estimates canopy interception (I) as the proportion of the day’s rain (P) that is intercepted by the vegetation canopy up to a limiting canopy carrying capacity (CC) in mm of rainfall. There are seven daily rainfall interception classes based on vegetation density and height; they are a proportion of the daily rainfall (P) as follows - nil, 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6. For each interception class, the SDI also estimates the amount of intercepted rain that is then evaporated from the canopy on each consecutive rainy day (I_w) in mm of rainfall. The remaining rain held in the canopy is entirely evaporated on the first rainless day (I_d) estimated in mm of rainfall. The three estimates of P, CC and I_w are provided for five forest canopy cover classes, three understory densities and two main forest forms in Table 1.

Table 1 Daily canopy interception loss (I) look-up table for different vegetation forms (from Mount 1972). For example, a eucalypt forest with light understory and 60% canopy cover produces the following estimates of CC and Iw for its P class as “0.4 to 2.8, 1.1” where 0.4 (P) is 40% of the day’s rain is intercepted up to a canopy capacity (CC) of 2.8 mm and 1.1 mm is evaporated each following rainy day (Iw). Note that all remaining moisture in the canopy dries on the first rainless day (Id).
Forest canopy cover	Eucalypts			Pines and rainforest
Forest canopy cover	Understory density class			Pines and rainforest
%	Nil (0%+)	Light (30%+)	Dense 60%+)	Light (30%+)
0+	Nil interception	0.1P to 0.6, 0.2	0.2P to 1.3, 0.5	0.2P to 1.3, 0.3
20+	0.1P to 0.6, 0.2	0.2P to 1.3, 0.5	0.3P to 2.0, 0.8	0.3P to 2.0, 0.5
40+	0.2P to 1.3, 0.5	0.3P to 2.0, 0.8	0.4P to 2.8, 1.1	0.4P to 2.8, 0.7
60+	0.3P to 2.0, 0.8	0.4P to 2.8, 1.1	0.5P to 3.6, 1.4	0.5P to 3.6, 0.9
80+	0.4P to 2.8, 1.1	0.5P to 3.6, 1.4	0.6P to 4.3, 1.7	0.6P to 4.3, 1.1

Once the contribution of rainfall to soil wetting was better accounted for through improved estimates of flash runoff and canopy interception, attention turned to soil drying.

Maximum temperature control of soil drying

Keetch and Byram (1968) introduced the idea that soils dry by transpiration and evaporation as determined by daily maximum temperature and five, rainfall related, soil drying curves. These five curves were replaced by a single set of five straight lines for average Tasmanian forests (Mount 1972). These five lines were confirmed by Langford, Duncan and Heeps (1977) for Melbourne’s water supply tall forests, though with different slopes and magnitude, and then by Burrows (1987) for Western Australian forests. The SDI replaces the KDBI tables with a single table of five successive straight lines, for all vegetation types and rainfalls, between logically determined stepped reductions in the rates that soil dries.

For each of the five straight lines, the following presents the way the soil dries by a combination of evaporation and/or plant transpiration and provides the SDI range for each line as used in Tasmania. For the first 25 mm of drying (SDI 0-25 mm), soil evaporation (E) helped plant transpiration (T) dry the soil both day and night. The soil dried at a slower rate for the next 25 mm (SDI 25-50 mm) because daytime soil surface evaporation was partially replenished every night. For SDI 50-140 mm plant transpiration (T) continued but soil evaporation (E) had ceased. For 140-165 mm SDI, daytime wilting, despite nightly recharge, caused much reduced transpiration. From 165 mm SDI onwards day and night wilting produced the smallest possible daily drying of the soil.

Generalising the SDI for wider application

The SDI was further refined to make it applicable more broadly. For example, to tune it for Tasmanian conditions, the SDI was amended to account for local evaporation rates. This was done by comparing available pan-evaporation rates from locations relevant to each catchment, in this case, Canberra and Hobart, which have long-term data sets. The SDI was also tailored for application in Western Australia and Victoria to account for differing forest transpiration rates and deeper soils.

Using rainfall runoff to test SDI accuracy

Soil dryness estimates the volume of rainwater the soil can absorb and hold before runoff commences. This means that, if the size of the rainfall event is known, an estimate of runoff from a catchment into its river can be made. This can be compared to observations of actual volumes at river gauges.

Testing both the KDBI and the SDI in the temperate catchments of Lidsdale, NSW and Emu River, Tasmania found that the KBDI regularly over-estimated run-off (ref?, Table 2). This means it under-estimated the soil dryness preceding the rain. The SDI’s estimate was very much closer to that observed runoff, especially for Tasmania’s Emu River.

Table 2. SDI and KBDI modelled estimates of annual catchment runoff as percentages of observed runoff, where 100% indicates the modelled runoff precisely estimated the observed runoff. Both modelled estimates used the same daily rainfall and maximum temperature input data. (Mount 1972)
Locations	Catchments of forest type	years	SDI as % of observed	average (%)	KBDI^b as % of observed	average (%)
Lidsdale, NSW	Eucalypts	2^a	98 & 124	100	152 & 484	178
Lidsdale, NSW	Mature Pines	2	103 & 107	103	205 & 1,659	252
Lidsdale, NSW	Young Pines	2	96 & 112	97	135 & 347	155
Emu River, Tas	Native Forest	4	100^b, 100, 100 & 99	100	116, 117, 129 & 116	118

^a Both Eucalypt years were used to model the one SDI for the other two Lidsdale forest types. KBDI Table 2 was used.

^b One Emu year was used to refine the Lidsdale SDI - which then fitted the other three years of Emu data. KBDI Table 5 was used.

[maybe add the Melbourne water runoff results here as well]

Calculating the Soil Dryness Index

[math formulas here?]

The Tasmanian Soil Dryness Index (SDI)

In Tasmania, the SDI is used to estimate how dry the soil is within zones about a 16 km radius from selected meteorological stations. These stations are mostly in valleys and are always clear of any vegetation taller than their 300 mm high rain gauge. Current dryness is measured as the depth of rain needed to fully wet the soil. For the SDI model, Tasmanian soils are assumed to average about a meter deep and be able to hold a little over 165 mm of rain before outflowing. See Figure 1 for a simplified representation of the SDI model as used in Tasmania.

Although evapotranspiration (ET) increases with altitude on the one hand, rainfall also increases, and temperature decreases on the other. These opposing drivers of soil dryness were addressed to good effect during the design of the Soil Dryness Index, in part, due to the position of the Emu River’s catchment at the approximate mid-altitude (650 m) of Tasmania’s forests and then supported by the accuracy of the run-off model. For these reasons, the Soil Dryness Index has been used in Tasmania for 50 years to calculate soil dryness at meteorological stations and delivered via the Tasmanian Fire Service’s daily Soil Dryness Index map.

Tasmanian uses of the SDI

The Tasmanian SDI estimates can be related to fire behaviour as soil dryness is related to vegetation dryness and hence flammability. The following table (Table 3) summarises this relationship and is used by the forest industry (ref).

Table 3. This table indicates the progressive flammability of Tasmanian vegetation types as they dry out. Vegetation dryness is assumed to be closely related to soil dryness as estimated by the Soil Dryness Index. As the SDI increases, more classes of dry vegetation can burn.

SDI	Can Burn If Dry
4+	Old button grass
13+	Open forest elevated logging slash
25+	Open forest floor litter (daytime)
50+	Open forest floor litter (day or night)
100+	Closed forest
140+	Dense forest (daytime)
165+	Dense forest (day or night)

Soils 5 to 13 mm dry. The dead leaves of Tasmania's Button Grass moorlands accumulate on stumps that keep them off the soil. This allows them to be burnt above wet soils from age four, only four days after rain. But as the soil dries past 13 mm, fires may invade the surrounding taller vegetation.

Soils 13 to 25 mm dry. Dry Eucalypt Forest selective logging debris can be burnt because much of it is raised above wet soils. This is usually called “Dry Forest top-disposal burning.”

Soils 25 to 50 mm dry. Dry Eucalypt Forest dead leaves accumulate at about one tonne per hectare per year. After 8 years they cover about 80% of the soil. The best time to burn this layer is when it dries each daytime then wets up overnight - which helps put the day’s fire out.

Soil more than 50 mm dry. Campers are happy when folding dry groundsheets. But this dryness should warn them to look around for fires that may have stayed alight all night. Past 50 mm dry forest fire-fighters know their under-ground fire engine has stopped helping. This is the ideal time to introduce the Fire Permit Period - not to stop fuel reduction burning, but for fire authorities to know where to prepare for possible escapes.

Soils more than 140 mm dry. Soils this dry can’t deliver water to tree leaves fast enough - so leaves wilt and droop and let the sun in to dry out fuels on the dry soil. Nearly all undisturbed “Wet” Forests have always been regenerated by fire for more than twelve million years - usually when over 140 mm dry. Fire’s deep heating of these very dry soils and the huge areas burnt are the reasons the tiny unprotected eucalypt seeds grow so quickly and that their seedlings are not all eaten. Logged “Wet” forests need fire’s same waste-disposal and soil heating effects as those unlogged - but waiting for soil to get to 140 mm dry is impactable. Fortunately, good regeneration of such logged areas is obtained if the soil is over 50 mm dry and if the coupe is large enough to minimize browsing effects.

Soils 165 -175 mm dry are about as dry as most Tasmanian soils get. Drought deaths start to occur. Heartwood in cracked trunks can be dry enough to be lit by small sparks so whole trees burn down.

References

Bell FC and Gatenby MT (1969) Effects of exotic softwoods afforestation on water yield. Water Res. Fnd. Australia. Bull. 15,

Burrows ND (1987) The Soil Dryness Index for use in fire control in the south-west of Western Australia. Department of Conservation and Land Management. Technical Report No. 17, Perth.

Keetch JJ and Byram GM (1968) A drought index for forest fire control. USDA Forest Service Res. Paper Se-38. 32 pp. Retrieved August 11, 2016 from http://www.srs.fs.usda.gov/pubs/viewpub.jsp?index=40

Keetch JJ and Byram GM

Langford KJ, Duncan HP and Heeps DF (1977) Evaluation and use of a water balance model. Institution of Engineers, Australia, Hydrology Symposium.

Mount AB (1972) The derivation and testing of a Soil Dryness Index using run-off data. Forestry Commission Tasmania. Bull. 4. (Imperial units)

Mount AB (1980) Estimation of evaporative losses from forests; a proven, simple model with wide applications. Hydrology & Water Resources Symposium. Adelaide (Metric units) (note errata: )

Rutter AJ (1963) Studies in the water relationships of Pinus sylvestris in plantation conditions. I. Measurement of rainfall and interception. Jour. Ecol. 51.

User:Tony Mount/sandbox