Extension of the scalar spherical harmonics for use with vector fields
In mathematics , vector spherical harmonics (VSH ) are an extension of the scalar spherical harmonics for use with vector fields . The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors .
Several conventions have been used to define the VSH.[ 1] [ 2] [ 3] [ 4] [ 5] et al. . Given a scalar spherical harmonic Yℓm (θ , φ )
Y
ℓ
m
=
Y
ℓ
m
r
^
,
{\displaystyle \mathbf {Y} _{\ell m}=Y_{\ell m}{\hat {\mathbf {r} }},}
Ψ
ℓ
m
=
r
∇
Y
ℓ
m
,
{\displaystyle \mathbf {\Psi } _{\ell m}=r\nabla Y_{\ell m},}
Φ
ℓ
m
=
r
×
∇
Y
ℓ
m
,
{\displaystyle \mathbf {\Phi } _{\ell m}=\mathbf {r} \times \nabla Y_{\ell m},}
with
r
^
{\displaystyle {\hat {\mathbf {r} }}}
unit vector along the radial direction in spherical coordinates and
r
{\displaystyle \mathbf {r} }
r
=
r
r
^
{\displaystyle \mathbf {r} =r{\hat {\mathbf {r} }}}
The interest of these new vector fields is to separate the radial dependence from the angular one when using spherical coordinates, so that a vector field admits a multipole expansion
E
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
(
E
ℓ
m
r
(
r
)
Y
ℓ
m
+
E
ℓ
m
(
1
)
(
r
)
Ψ
ℓ
m
+
E
ℓ
m
(
2
)
(
r
)
Φ
ℓ
m
)
.
{\displaystyle \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left(E_{\ell m}^{r}(r)\mathbf {Y} _{\ell m}+E_{\ell m}^{(1)}(r)\mathbf {\Psi } _{\ell m}+E_{\ell m}^{(2)}(r)\mathbf {\Phi } _{\ell m}\right).}
The labels on the components reflect that
E
ℓ
m
r
{\displaystyle E_{\ell m}^{r}}
E
ℓ
m
(
1
)
{\displaystyle E_{\ell m}^{(1)}}
E
ℓ
m
(
2
)
{\displaystyle E_{\ell m}^{(2)}}
r
{\displaystyle \mathbf {r} }
Like the scalar spherical harmonics, the VSH satisfy
Y
ℓ
,
−
m
=
(
−
1
)
m
Y
ℓ
m
∗
,
Ψ
ℓ
,
−
m
=
(
−
1
)
m
Ψ
ℓ
m
∗
,
Φ
ℓ
,
−
m
=
(
−
1
)
m
Φ
ℓ
m
∗
,
{\displaystyle {\begin{aligned}\mathbf {Y} _{\ell ,-m}&=(-1)^{m}\mathbf {Y} _{\ell m}^{*},\\\mathbf {\Psi } _{\ell ,-m}&=(-1)^{m}\mathbf {\Psi } _{\ell m}^{*},\\\mathbf {\Phi } _{\ell ,-m}&=(-1)^{m}\mathbf {\Phi } _{\ell m}^{*},\end{aligned}}}
which cuts the number of independent functions roughly in half. The star indicates complex conjugation .
The VSH are orthogonal in the usual three-dimensional way at each point
r
{\displaystyle \mathbf {r} }
Y
ℓ
m
(
r
)
⋅
Ψ
ℓ
m
(
r
)
=
0
,
Y
ℓ
m
(
r
)
⋅
Φ
ℓ
m
(
r
)
=
0
,
Ψ
ℓ
m
(
r
)
⋅
Φ
ℓ
m
(
r
)
=
0.
{\displaystyle {\begin{aligned}\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Psi } _{\ell m}(\mathbf {r} )&=0,\\\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell m}(\mathbf {r} )&=0,\\\mathbf {\Psi } _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell m}(\mathbf {r} )&=0.\end{aligned}}}
They are also orthogonal in Hilbert space:
∫
Y
ℓ
m
⋅
Y
ℓ
′
m
′
∗
d
Ω
=
δ
ℓ
ℓ
′
δ
m
m
′
,
∫
Ψ
ℓ
m
⋅
Ψ
ℓ
′
m
′
∗
d
Ω
=
ℓ
(
ℓ
+
1
)
δ
ℓ
ℓ
′
δ
m
m
′
,
∫
Φ
ℓ
m
⋅
Φ
ℓ
′
m
′
∗
d
Ω
=
ℓ
(
ℓ
+
1
)
δ
ℓ
ℓ
′
δ
m
m
′
,
∫
Y
ℓ
m
⋅
Ψ
ℓ
′
m
′
∗
d
Ω
=
0
,
∫
Y
ℓ
m
⋅
Φ
ℓ
′
m
′
∗
d
Ω
=
0
,
∫
Ψ
ℓ
m
⋅
Φ
ℓ
′
m
′
∗
d
Ω
=
0.
{\displaystyle {\begin{aligned}\int \mathbf {Y} _{\ell m}\cdot \mathbf {Y} _{\ell 'm'}^{*}\,d\Omega &=\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {\Psi } _{\ell m}\cdot \mathbf {\Psi } _{\ell 'm'}^{*}\,d\Omega &=\ell (\ell +1)\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {\Phi } _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm'}^{*}\,d\Omega &=\ell (\ell +1)\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {Y} _{\ell m}\cdot \mathbf {\Psi } _{\ell 'm'}^{*}\,d\Omega &=0,\\\int \mathbf {Y} _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm'}^{*}\,d\Omega &=0,\\\int \mathbf {\Psi } _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm'}^{*}\,d\Omega &=0.\end{aligned}}}
An additional result at a single point
r
{\displaystyle \mathbf {r} }
ℓ
,
m
,
ℓ
′
,
m
′
{\displaystyle \ell ,m,\ell ',m'}
Y
ℓ
m
(
r
)
⋅
Ψ
ℓ
′
m
′
(
r
)
=
0
,
Y
ℓ
m
(
r
)
⋅
Φ
ℓ
′
m
′
(
r
)
=
0.
{\displaystyle {\begin{aligned}\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Psi } _{\ell 'm'}(\mathbf {r} )&=0,\\\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell 'm'}(\mathbf {r} )&=0.\end{aligned}}}
Vector multipole moments [ edit ] The orthogonality relations allow one to compute the spherical multipole moments of a vector field as
E
ℓ
m
r
=
∫
E
⋅
Y
ℓ
m
∗
d
Ω
,
E
ℓ
m
(
1
)
=
1
ℓ
(
ℓ
+
1
)
∫
E
⋅
Ψ
ℓ
m
∗
d
Ω
,
E
ℓ
m
(
2
)
=
1
ℓ
(
ℓ
+
1
)
∫
E
⋅
Φ
ℓ
m
∗
d
Ω
.
{\displaystyle {\begin{aligned}E_{\ell m}^{r}&=\int \mathbf {E} \cdot \mathbf {Y} _{\ell m}^{*}\,d\Omega ,\\E_{\ell m}^{(1)}&={\frac {1}{\ell (\ell +1)}}\int \mathbf {E} \cdot \mathbf {\Psi } _{\ell m}^{*}\,d\Omega ,\\E_{\ell m}^{(2)}&={\frac {1}{\ell (\ell +1)}}\int \mathbf {E} \cdot \mathbf {\Phi } _{\ell m}^{*}\,d\Omega .\end{aligned}}}
The gradient of a scalar field [ edit ] Given the multipole expansion of a scalar field
ϕ
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
ϕ
ℓ
m
(
r
)
Y
ℓ
m
(
θ
,
ϕ
)
,
{\displaystyle \phi =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\phi _{\ell m}(r)Y_{\ell m}(\theta ,\phi ),}
we can express its gradient in terms of the VSH as
∇
ϕ
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
(
d
ϕ
ℓ
m
d
r
Y
ℓ
m
+
ϕ
ℓ
m
r
Ψ
ℓ
m
)
.
{\displaystyle \nabla \phi =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {d\phi _{\ell m}}{dr}}\mathbf {Y} _{\ell m}+{\frac {\phi _{\ell m}}{r}}\mathbf {\Psi } _{\ell m}\right).}
For any multipole field we have
∇
⋅
(
f
(
r
)
Y
ℓ
m
)
=
(
d
f
d
r
+
2
r
f
)
Y
ℓ
m
,
∇
⋅
(
f
(
r
)
Ψ
ℓ
m
)
=
−
ℓ
(
ℓ
+
1
)
r
f
Y
ℓ
m
,
∇
⋅
(
f
(
r
)
Φ
ℓ
m
)
=
0.
{\displaystyle {\begin{aligned}\nabla \cdot \left(f(r)\mathbf {Y} _{\ell m}\right)&=\left({\frac {df}{dr}}+{\frac {2}{r}}f\right)Y_{\ell m},\\\nabla \cdot \left(f(r)\mathbf {\Psi } _{\ell m}\right)&=-{\frac {\ell (\ell +1)}{r}}fY_{\ell m},\\\nabla \cdot \left(f(r)\mathbf {\Phi } _{\ell m}\right)&=0.\end{aligned}}}
By superposition we obtain the divergence of any vector field:
∇
⋅
E
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
(
d
E
ℓ
m
r
d
r
+
2
r
E
ℓ
m
r
−
ℓ
(
ℓ
+
1
)
r
E
ℓ
m
(
1
)
)
Y
ℓ
m
.
{\displaystyle \nabla \cdot \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {dE_{\ell m}^{r}}{dr}}+{\frac {2}{r}}E_{\ell m}^{r}-{\frac {\ell (\ell +1)}{r}}E_{\ell m}^{(1)}\right)Y_{\ell m}.}
We see that the component on Φ ℓm solenoidal .
For any multipole field we have
∇
×
(
f
(
r
)
Y
ℓ
m
)
=
−
1
r
f
Φ
ℓ
m
,
∇
×
(
f
(
r
)
Ψ
ℓ
m
)
=
(
d
f
d
r
+
1
r
f
)
Φ
ℓ
m
,
∇
×
(
f
(
r
)
Φ
ℓ
m
)
=
−
ℓ
(
ℓ
+
1
)
r
f
Y
ℓ
m
−
(
d
f
d
r
+
1
r
f
)
Ψ
ℓ
m
.
{\displaystyle {\begin{aligned}\nabla \times \left(f(r)\mathbf {Y} _{\ell m}\right)&=-{\frac {1}{r}}f\mathbf {\Phi } _{\ell m},\\\nabla \times \left(f(r)\mathbf {\Psi } _{\ell m}\right)&=\left({\frac {df}{dr}}+{\frac {1}{r}}f\right)\mathbf {\Phi } _{\ell m},\\\nabla \times \left(f(r)\mathbf {\Phi } _{\ell m}\right)&=-{\frac {\ell (\ell +1)}{r}}f\mathbf {Y} _{\ell m}-\left({\frac {df}{dr}}+{\frac {1}{r}}f\right)\mathbf {\Psi } _{\ell m}.\end{aligned}}}
By superposition we obtain the curl of any vector field:
∇
×
E
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
(
−
ℓ
(
ℓ
+
1
)
r
E
ℓ
m
(
2
)
Y
ℓ
m
−
(
d
E
ℓ
m
(
2
)
d
r
+
1
r
E
ℓ
m
(
2
)
)
Ψ
ℓ
m
+
(
−
1
r
E
ℓ
m
r
+
d
E
ℓ
m
(
1
)
d
r
+
1
r
E
ℓ
m
(
1
)
)
Φ
ℓ
m
)
.
{\displaystyle \nabla \times \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left(-{\frac {\ell (\ell +1)}{r}}E_{\ell m}^{(2)}\mathbf {Y} _{\ell m}-\left({\frac {dE_{\ell m}^{(2)}}{dr}}+{\frac {1}{r}}E_{\ell m}^{(2)}\right)\mathbf {\Psi } _{\ell m}+\left(-{\frac {1}{r}}E_{\ell m}^{r}+{\frac {dE_{\ell m}^{(1)}}{dr}}+{\frac {1}{r}}E_{\ell m}^{(1)}\right)\mathbf {\Phi } _{\ell m}\right).}
The action of the Laplace operator
Δ
=
∇
⋅
∇
{\displaystyle \Delta =\nabla \cdot \nabla }
Δ
(
f
(
r
)
Z
ℓ
m
)
=
(
1
r
2
∂
∂
r
r
2
∂
f
∂
r
)
Z
ℓ
m
+
f
(
r
)
Δ
Z
ℓ
m
,
{\displaystyle \Delta \left(f(r)\mathbf {Z} _{\ell m}\right)=\left({\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}r^{2}{\frac {\partial f}{\partial r}}\right)\mathbf {Z} _{\ell m}+f(r)\Delta \mathbf {Z} _{\ell m},}
Z
ℓ
m
=
Y
ℓ
m
,
Ψ
ℓ
m
,
Φ
ℓ
m
{\displaystyle \mathbf {Z} _{\ell m}=\mathbf {Y} _{\ell m},\mathbf {\Psi } _{\ell m},\mathbf {\Phi } _{\ell m}}
Δ
Y
ℓ
m
=
−
1
r
2
(
2
+
ℓ
(
ℓ
+
1
)
)
Y
ℓ
m
+
2
r
2
Ψ
ℓ
m
,
Δ
Ψ
ℓ
m
=
2
r
2
ℓ
(
ℓ
+
1
)
Y
ℓ
m
−
1
r
2
ℓ
(
ℓ
+
1
)
Ψ
ℓ
m
,
Δ
Φ
ℓ
m
=
−
1
r
2
ℓ
(
ℓ
+
1
)
Φ
ℓ
m
.
{\displaystyle {\begin{aligned}\Delta \mathbf {Y} _{\ell m}&=-{\frac {1}{r^{2}}}(2+\ell (\ell +1))\mathbf {Y} _{\ell m}+{\frac {2}{r^{2}}}\mathbf {\Psi } _{\ell m},\\\Delta \mathbf {\Psi } _{\ell m}&={\frac {2}{r^{2}}}\ell (\ell +1)\mathbf {Y} _{\ell m}-{\frac {1}{r^{2}}}\ell (\ell +1)\mathbf {\Psi } _{\ell m},\\\Delta \mathbf {\Phi } _{\ell m}&=-{\frac {1}{r^{2}}}\ell (\ell +1)\mathbf {\Phi } _{\ell m}.\end{aligned}}}
Also note that this action becomes symmetric , i.e. the off-diagonal coefficients are equal to
2
r
2
ℓ
(
ℓ
+
1
)
{\textstyle {\frac {2}{r^{2}}}{\sqrt {\ell (\ell +1)}}}
normalized VSH.
First vector spherical harmonics [ edit ]
ℓ
=
0
{\displaystyle \ell =0}
Y
00
=
1
4
π
r
^
,
Ψ
00
=
0
,
Φ
00
=
0
.
{\displaystyle {\begin{aligned}\mathbf {Y} _{00}&={\sqrt {\frac {1}{4\pi }}}{\hat {\mathbf {r} }},\\\mathbf {\Psi } _{00}&=\mathbf {0} ,\\\mathbf {\Phi } _{00}&=\mathbf {0} .\end{aligned}}}
ℓ
=
1
{\displaystyle \ell =1}
Y
10
=
3
4
π
cos
θ
r
^
,
Y
11
=
−
3
8
π
e
i
φ
sin
θ
r
^
,
{\displaystyle {\begin{aligned}\mathbf {Y} _{10}&={\sqrt {\frac {3}{4\pi }}}\cos \theta \,{\hat {\mathbf {r} }},\\\mathbf {Y} _{11}&=-{\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\sin \theta \,{\hat {\mathbf {r} }},\end{aligned}}}
Ψ
10
=
−
3
4
π
sin
θ
θ
^
,
Ψ
11
=
−
3
8
π
e
i
φ
(
cos
θ
θ
^
+
i
φ
^
)
,
{\displaystyle {\begin{aligned}\mathbf {\Psi } _{10}&=-{\sqrt {\frac {3}{4\pi }}}\sin \theta \,{\hat {\mathbf {\theta } }},\\\mathbf {\Psi } _{11}&=-{\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\left(\cos \theta \,{\hat {\mathbf {\theta } }}+i\,{\hat {\mathbf {\varphi } }}\right),\end{aligned}}}
Φ
10
=
−
3
4
π
sin
θ
φ
^
,
Φ
11
=
3
8
π
e
i
φ
(
i
θ
^
−
cos
θ
φ
^
)
.
{\displaystyle {\begin{aligned}\mathbf {\Phi } _{10}&=-{\sqrt {\frac {3}{4\pi }}}\sin \theta \,{\hat {\mathbf {\varphi } }},\\\mathbf {\Phi } _{11}&={\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\left(i\,{\hat {\mathbf {\theta } }}-\cos \theta \,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}}
ℓ
=
2
{\displaystyle \ell =2}
Y
20
=
1
4
5
π
(
3
cos
2
θ
−
1
)
r
^
,
Y
21
=
−
15
8
π
sin
θ
cos
θ
e
i
φ
r
^
,
Y
22
=
1
4
15
2
π
sin
2
θ
e
2
i
φ
r
^
.
{\displaystyle {\begin{aligned}\mathbf {Y} _{20}&={\frac {1}{4}}{\sqrt {\frac {5}{\pi }}}\,(3\cos ^{2}\theta -1)\,{\hat {\mathbf {r} }},\\\mathbf {Y} _{21}&=-{\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,\cos \theta \,e^{i\varphi }\,{\hat {\mathbf {r} }},\\\mathbf {Y} _{22}&={\frac {1}{4}}{\sqrt {\frac {15}{2\pi }}}\,\sin ^{2}\theta \,e^{2i\varphi }\,{\hat {\mathbf {r} }}.\end{aligned}}}
Ψ
20
=
−
3
2
5
π
sin
θ
cos
θ
θ
^
,
Ψ
21
=
−
15
8
π
e
i
φ
(
cos
2
θ
θ
^
+
i
cos
θ
φ
^
)
,
Ψ
22
=
15
8
π
sin
θ
e
2
i
φ
(
cos
θ
θ
^
+
i
φ
^
)
.
{\displaystyle {\begin{aligned}\mathbf {\Psi } _{20}&=-{\frac {3}{2}}{\sqrt {\frac {5}{\pi }}}\,\sin \theta \,\cos \theta \,{\hat {\mathbf {\theta } }},\\\mathbf {\Psi } _{21}&=-{\sqrt {\frac {15}{8\pi }}}\,e^{i\varphi }\,\left(\cos 2\theta \,{\hat {\mathbf {\theta } }}+i\cos \theta \,{\hat {\mathbf {\varphi } }}\right),\\\mathbf {\Psi } _{22}&={\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,e^{2i\varphi }\,\left(\cos \theta \,{\hat {\mathbf {\theta } }}+i\,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}}
Φ
20
=
−
3
2
5
π
sin
θ
cos
θ
φ
^
,
Φ
21
=
15
8
π
e
i
φ
(
i
cos
θ
θ
^
−
cos
2
θ
φ
^
)
,
Φ
22
=
15
8
π
sin
θ
e
2
i
φ
(
−
i
θ
^
+
cos
θ
φ
^
)
.
{\displaystyle {\begin{aligned}\mathbf {\Phi } _{20}&=-{\frac {3}{2}}{\sqrt {\frac {5}{\pi }}}\sin \theta \,\cos \theta \,{\hat {\mathbf {\varphi } }},\\\mathbf {\Phi } _{21}&={\sqrt {\frac {15}{8\pi }}}\,e^{i\varphi }\,\left(i\cos \theta \,{\hat {\mathbf {\theta } }}-\cos 2\theta \,{\hat {\mathbf {\varphi } }}\right),\\\mathbf {\Phi } _{22}&={\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,e^{2i\varphi }\,\left(-i\,{\hat {\mathbf {\theta } }}+\cos \theta \,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}}
Expressions for negative values of m are obtained by applying the symmetry relations.
The VSH are especially useful in the study of multipole radiation fields . For instance, a magnetic multipole is due to an oscillating current with angular frequency
ω
{\displaystyle \omega }
J
^
=
J
(
r
)
Φ
ℓ
m
,
{\displaystyle {\hat {\mathbf {J} }}=J(r)\mathbf {\Phi } _{\ell m},}
and the corresponding electric and magnetic fields, can be written as
E
^
=
E
(
r
)
Φ
ℓ
m
,
B
^
=
B
r
(
r
)
Y
ℓ
m
+
B
(
1
)
(
r
)
Ψ
ℓ
m
.
{\displaystyle {\begin{aligned}{\hat {\mathbf {E} }}&=E(r)\mathbf {\Phi } _{\ell m},\\{\hat {\mathbf {B} }}&=B^{r}(r)\mathbf {Y} _{\ell m}+B^{(1)}(r)\mathbf {\Psi } _{\ell m}.\end{aligned}}}
Substituting into Maxwell equations, Gauss's law is automatically satisfied
∇
⋅
E
^
=
0
,
{\displaystyle \nabla \cdot {\hat {\mathbf {E} }}=0,}
while Faraday's law decouples as
∇
×
E
^
=
−
i
ω
B
^
⇒
{
ℓ
(
ℓ
+
1
)
r
E
=
i
ω
B
r
,
d
E
d
r
+
E
r
=
i
ω
B
(
1
)
.
{\displaystyle \nabla \times {\hat {\mathbf {E} }}=-i\omega {\hat {\mathbf {B} }}\quad \Rightarrow \quad {\begin{cases}{\dfrac {\ell (\ell +1)}{r}}E=i\omega B^{r},\\{\dfrac {dE}{dr}}+{\dfrac {E}{r}}=i\omega B^{(1)}.\end{cases}}}
Gauss' law for the magnetic field implies
∇
⋅
B
^
=
0
⇒
d
B
r
d
r
+
2
r
B
r
−
ℓ
(
ℓ
+
1
)
r
B
(
1
)
=
0
,
{\displaystyle \nabla \cdot {\hat {\mathbf {B} }}=0\quad \Rightarrow \quad {\frac {dB^{r}}{dr}}+{\frac {2}{r}}B^{r}-{\frac {\ell (\ell +1)}{r}}B^{(1)}=0,}
and Ampère–Maxwell's equation gives
∇
×
B
^
=
μ
0
J
^
+
i
μ
0
ε
0
ω
E
^
⇒
−
B
r
r
+
d
B
(
1
)
d
r
+
B
(
1
)
r
=
μ
0
J
+
i
ω
μ
0
ε
0
E
.
{\displaystyle \nabla \times {\hat {\mathbf {B} }}=\mu _{0}{\hat {\mathbf {J} }}+i\mu _{0}\varepsilon _{0}\omega {\hat {\mathbf {E} }}\quad \Rightarrow \quad -{\frac {B^{r}}{r}}+{\frac {dB^{(1)}}{dr}}+{\frac {B^{(1)}}{r}}=\mu _{0}J+i\omega \mu _{0}\varepsilon _{0}E.}
In this way, the partial differential equations have been transformed into a set of ordinary differential equations.
Alternative definition [ edit ] Angular part of magnetic and electric vector spherical harmonics. Red and green arrows show the direction of the field. Generating scalar functions are also presented, only the first three orders are shown (dipoles, quadrupoles, octupoles). In many applications, vector spherical harmonics are defined as fundamental set of the solutions of vector Helmholtz equation in spherical coordinates.[ 6] [ 7]
In this case, vector spherical harmonics are generated by scalar functions, which are solutions of scalar Helmholtz equation with the wavevector
k
{\displaystyle \mathbf {k} }
ψ
e
m
n
=
cos
m
φ
P
n
m
(
cos
ϑ
)
z
n
(
k
r
)
ψ
o
m
n
=
sin
m
φ
P
n
m
(
cos
ϑ
)
z
n
(
k
r
)
{\displaystyle {\begin{array}{l}{\psi _{emn}=\cos m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}\\{\psi _{omn}=\sin m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}\end{array}}}
P
n
m
(
cos
θ
)
{\displaystyle P_{n}^{m}(\cos \theta )}
associated Legendre polynomials , and
z
n
(
k
r
)
{\displaystyle z_{n}({k}r)}
spherical Bessel functions .
Vector spherical harmonics are defined as:
longitudinal harmonics
L
o
e
m
n
=
∇
ψ
o
e
m
n
{\displaystyle \mathbf {L} _{^{e}_{o}mn}=\mathbf {\nabla } \psi _{^{e}_{o}mn}}
magnetic harmonics
M
o
e
m
n
=
∇
×
(
r
ψ
o
e
m
n
)
{\displaystyle \mathbf {M} _{^{e}_{o}mn}=\nabla \times \left(\mathbf {r} \psi _{^{e}_{o}mn}\right)}
electric harmonics
N
o
e
m
n
=
∇
×
M
o
e
m
n
k
{\displaystyle \mathbf {N} _{^{e}_{o}mn}={\frac {\nabla \times \mathbf {M} _{^{e}_{o}mn}}{k}}}
Here we use harmonics real-valued angular part, where
m
≥
0
{\displaystyle m\geq 0}
Let us introduce the notation
ρ
=
k
r
{\displaystyle \rho =kr}
M
e
m
n
(
k
,
r
)
=
−
m
sin
(
θ
)
sin
(
m
φ
)
P
n
m
(
cos
(
θ
)
)
z
n
(
ρ
)
e
θ
−
cos
(
m
φ
)
d
P
n
m
(
cos
(
θ
)
)
d
θ
z
n
(
ρ
)
e
φ
{\displaystyle {\begin{aligned}{\mathbf {M} _{emn}(k,\mathbf {r} )=\qquad {{\frac {-m}{\sin(\theta )}}\sin(m\varphi )P_{n}^{m}(\cos(\theta ))}z_{n}(\rho )\mathbf {e} _{\theta }}\\{{}-\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}z_{n}(\rho )\mathbf {e} _{\varphi }\end{aligned}}}
M
o
m
n
(
k
,
r
)
=
m
sin
(
θ
)
cos
(
m
φ
)
P
n
m
(
cos
(
θ
)
)
z
n
(
ρ
)
e
θ
−
sin
(
m
φ
)
d
P
n
m
(
cos
(
θ
)
)
d
θ
z
n
(
ρ
)
e
φ
{\displaystyle {\begin{aligned}{\mathbf {M} _{omn}(k,\mathbf {r} )=\qquad {{\frac {m}{\sin(\theta )}}\cos(m\varphi )P_{n}^{m}(\cos(\theta ))}}z_{n}(\rho )\mathbf {e} _{\theta }\\{{}-\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}z_{n}(\rho )\mathbf {e} _{\varphi }}\end{aligned}}}
N
e
m
n
(
k
,
r
)
=
z
n
(
ρ
)
ρ
cos
(
m
φ
)
n
(
n
+
1
)
P
n
m
(
cos
(
θ
)
)
e
r
+
cos
(
m
φ
)
d
P
n
m
(
cos
(
θ
)
)
d
θ
1
ρ
d
d
ρ
[
ρ
z
n
(
ρ
)
]
e
θ
−
m
sin
(
m
φ
)
P
n
m
(
cos
(
θ
)
)
sin
(
θ
)
1
ρ
d
d
ρ
[
ρ
z
n
(
ρ
)
]
e
φ
{\displaystyle {\begin{aligned}{\mathbf {N} _{emn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\cos(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }}\\{{}+\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{{}-m\sin(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}}
N
o
m
n
(
k
,
r
)
=
z
n
(
ρ
)
ρ
sin
(
m
φ
)
n
(
n
+
1
)
P
n
m
(
cos
(
θ
)
)
e
r
+
sin
(
m
φ
)
d
P
n
m
(
cos
(
θ
)
)
d
θ
1
ρ
d
d
ρ
[
ρ
z
n
(
ρ
)
]
e
θ
+
m
cos
(
m
φ
)
P
n
m
(
cos
(
θ
)
)
sin
(
θ
)
1
ρ
d
d
ρ
[
ρ
z
n
(
ρ
)
]
e
φ
{\displaystyle {\begin{aligned}\mathbf {N} _{omn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\sin(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }\\{}+\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{}+{m\cos(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}}
ρ
{\displaystyle \rho }
ρ
{\displaystyle \rho }
Longitudinal harmonics:
L
o
e
m
n
(
k
,
r
)
=
∂
∂
r
z
n
(
k
r
)
P
n
m
(
cos
θ
)
sin
cos
m
φ
e
r
+
1
r
z
n
(
k
r
)
∂
∂
θ
P
n
m
(
cos
θ
)
sin
cos
m
φ
e
θ
∓
m
r
sin
θ
z
n
(
k
r
)
P
n
m
(
cos
θ
)
cos
sin
m
φ
e
φ
{\displaystyle {\begin{aligned}\mathbf {L} _{^{e}_{o}{mn}}(k,\mathbf {r} ){}=\qquad &{\frac {\partial }{\partial r}}z_{n}(kr)P_{n}^{m}(\cos \theta ){^{\cos }_{\sin }}{m\varphi }\mathbf {e} _{r}\\{}+{}&{\frac {1}{r}}z_{n}(kr){\frac {\partial }{\partial \theta }}P_{n}^{m}(\cos \theta ){^{\cos }_{\sin }}m\varphi \mathbf {e} _{\theta }\\{}\mp {}&{\frac {m}{r\sin \theta }}z_{n}(kr)P_{n}^{m}(\cos \theta ){^{\sin }_{\cos }}m\varphi \mathbf {e} _{\varphi }\end{aligned}}}
The solutions of the Helmholtz vector equation obey the following orthogonality relations:[ 7]
∫
0
2
π
∫
0
π
L
o
e
m
n
⋅
L
o
e
m
n
sin
ϑ
d
ϑ
d
φ
=
(
1
+
δ
m
,
0
)
2
π
(
2
n
+
1
)
2
(
n
+
m
)
!
(
n
−
m
)
!
k
2
{
n
[
z
n
−
1
(
k
r
)
]
2
+
(
n
+
1
)
[
z
n
+
1
(
k
r
)
]
2
}
∫
0
2
π
∫
0
π
M
o
e
m
n
⋅
M
o
e
m
n
sin
ϑ
d
ϑ
d
φ
=
(
1
+
δ
m
,
0
)
2
π
2
n
+
1
(
n
+
m
)
!
(
n
−
m
)
!
n
(
n
+
1
)
[
z
n
(
k
r
)
]
2
∫
0
2
π
∫
0
π
N
o
e
m
n
⋅
N
o
e
m
n
sin
ϑ
d
ϑ
d
φ
=
(
1
+
δ
m
,
0
)
2
π
(
2
n
+
1
)
2
(
n
+
m
)
!
(
n
−
m
)
!
n
(
n
+
1
)
{
(
n
+
1
)
[
z
n
−
1
(
k
r
)
]
2
+
n
[
z
n
+
1
(
k
r
)
]
2
}
∫
0
π
∫
0
2
π
L
o
e
m
n
⋅
N
o
e
m
n
sin
ϑ
d
ϑ
d
φ
=
(
1
+
δ
m
,
0
)
2
π
(
2
n
+
1
)
2
(
n
+
m
)
!
(
n
−
m
)
!
n
(
n
+
1
)
k
{
[
z
n
−
1
(
k
r
)
]
2
−
[
z
n
+
1
(
k
r
)
]
2
}
{\displaystyle {\begin{aligned}\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {L} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}k^{2}\left\{n\left[z_{n-1}(kr)\right]^{2}+(n+1)\left[z_{n+1}(kr)\right]^{2}\right\}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {M} _{^{e}_{o}mn}\cdot \mathbf {M} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{2n+1}}{\frac {(n+m)!}{(n-m)!}}n(n+1)\left[z_{n}(kr)\right]^{2}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {N} _{^{e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}n(n+1)\left\{(n+1)\left[z_{n-1}(kr)\right]^{2}+n\left[z_{n+1}(kr)\right]^{2}\right\}\\[3pt]\int _{0}^{\pi }\int _{0}^{2\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}n(n+1)k\left\{\left[z_{n-1}(kr)\right]^{2}-\left[z_{n+1}(kr)\right]^{2}\right\}\end{aligned}}}
All other integrals over the angles between different functions or functions with different indices are equal to zero.
Rotation and inversion [ edit ] Illustration of the transformation of vector spherical harmonics under rotations. One can see that they are transformed in the same way as the corresponding scalar functions. Under rotation, vector spherical harmonics are transformed through each other in the same way as the corresponding scalar spherical functions , which are generating for a specific type of vector harmonics. For example, if the generating functions are the usual spherical harmonics , then the vector harmonics will also be transformed through the Wigner D-matrices [ 8] [ 9] [ 10]
D
^
(
α
,
β
,
γ
)
Y
J
M
(
s
)
(
θ
,
φ
)
=
∑
M
′
=
−
J
J
[
D
M
M
′
(
J
)
(
α
,
β
,
γ
)
]
∗
Y
J
M
′
(
s
)
(
θ
,
φ
)
,
{\displaystyle {\hat {D}}(\alpha ,\beta ,\gamma )\mathbf {Y} _{JM}^{(s)}(\theta ,\varphi )=\sum _{M'=-J}^{J}[D_{MM'}^{(J)}(\alpha ,\beta ,\gamma )]^{*}\mathbf {Y} _{JM'}^{(s)}(\theta ,\varphi ),}
Under inversion, electric and longitudinal spherical harmonics behave in the same way as scalar spherical functions, i.e.
I
^
N
J
M
(
θ
,
φ
)
=
(
−
1
)
J
N
J
M
(
θ
,
φ
)
,
{\displaystyle {\hat {I}}\mathbf {N} _{JM}(\theta ,\varphi )=(-1)^{J}\mathbf {N} _{JM}(\theta ,\varphi ),}
I
^
M
J
M
(
θ
,
φ
)
=
(
−
1
)
J
+
1
M
J
M
(
θ
,
φ
)
,
{\displaystyle {\hat {I}}\mathbf {M} _{JM}(\theta ,\varphi )=(-1)^{J+1}\mathbf {M} _{JM}(\theta ,\varphi ),}
In the calculation of the Stokes' law for the drag that a viscous fluid exerts on a small spherical particle, the velocity distribution obeys Navier–Stokes equations neglecting inertia, i.e.,
0
=
∇
⋅
v
,
0
=
−
∇
p
+
η
∇
2
v
,
{\displaystyle {\begin{aligned}0&=\nabla \cdot \mathbf {v} ,\\\mathbf {0} &=-\nabla p+\eta \nabla ^{2}\mathbf {v} ,\end{aligned}}}
with the boundary conditions
v
=
{
0
r
=
a
,
−
U
0
r
→
∞
.
{\displaystyle \mathbf {v} ={\begin{cases}\mathbf {0} &r=a,\\-\mathbf {U} _{0}&r\to \infty .\end{cases}}}
where U is the relative velocity of the particle to the fluid far from the particle. In spherical coordinates this velocity at infinity can be written as
U
0
=
U
0
(
cos
θ
r
^
−
sin
θ
θ
^
)
=
U
0
(
Y
10
+
Ψ
10
)
.
{\displaystyle \mathbf {U} _{0}=U_{0}\left(\cos \theta \,{\hat {\mathbf {r} }}-\sin \theta \,{\hat {\mathbf {\theta } }}\right)=U_{0}\left(\mathbf {Y} _{10}+\mathbf {\Psi } _{10}\right).}
The last expression suggests an expansion in spherical harmonics for the liquid velocity and the pressure
p
=
p
(
r
)
Y
10
,
v
=
v
r
(
r
)
Y
10
+
v
(
1
)
(
r
)
Ψ
10
.
{\displaystyle {\begin{aligned}p&=p(r)Y_{10},\\\mathbf {v} &=v^{r}(r)\mathbf {Y} _{10}+v^{(1)}(r)\mathbf {\Psi } _{10}.\end{aligned}}}
Substitution in the Navier–Stokes equations produces a set of ordinary differential equations for the coefficients.
Here the following definitions are used:
Y
e
m
n
=
cos
m
φ
P
n
m
(
cos
θ
)
Y
o
m
n
=
sin
m
φ
P
n
m
(
cos
θ
)
{\displaystyle {\begin{aligned}Y_{emn}&=\cos m\varphi P_{n}^{m}(\cos \theta )\\Y_{omn}&=\sin m\varphi P_{n}^{m}(\cos \theta )\end{aligned}}}
X
o
e
m
n
(
k
k
)
=
∇
×
(
k
Y
e
o
m
n
(
k
k
)
)
{\displaystyle \mathbf {X} _{^{e}_{o}mn}\left({\frac {\mathbf {k} }{k}}\right)=\nabla \times \left(\mathbf {k} Y_{^{o}_{e}mn}\left({\frac {\mathbf {k} }{k}}\right)\right)}
Z
e
o
m
n
(
k
k
)
=
i
k
k
×
X
o
e
m
n
(
k
k
)
{\displaystyle \mathbf {Z} _{^{o}_{e}mn}\left({\frac {\mathbf {k} }{k}}\right)=i{\frac {\mathbf {k} }{k}}\times \mathbf {X} _{^{e}_{o}mn}\left({\frac {\mathbf {k} }{k}}\right)}
z
n
{\displaystyle z_{n}}
spherical Bessel functions , with help of plane wave expansion one can obtain the following integral relations:[ 11]
N
p
m
n
(
1
)
(
k
,
r
)
=
i
−
n
4
π
∫
Z
p
m
n
(
k
k
)
e
i
k
⋅
r
d
Ω
k
{\displaystyle \mathbf {N} _{pmn}^{(1)}(k,\mathbf {r} )={\frac {i^{-n}}{4\pi }}\int \mathbf {Z} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)e^{i\mathbf {k} \cdot \mathbf {r} }d\Omega _{k}}
M
p
m
n
(
1
)
(
k
,
r
)
=
i
−
n
4
π
∫
X
p
m
n
(
k
k
)
e
i
k
⋅
r
d
Ω
k
{\displaystyle \mathbf {M} _{pmn}^{(1)}(k,\mathbf {r} )={\frac {i^{-n}}{4\pi }}\int \mathbf {X} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)e^{i\mathbf {k} \cdot \mathbf {r} }d\Omega _{k}}
In case, when
z
n
{\displaystyle z_{n}}
[ 12] [ 11]
M
p
m
n
(
3
)
(
k
,
r
)
=
i
−
n
2
π
k
∬
−
∞
∞
d
k
‖
e
i
(
k
x
x
+
k
y
y
±
k
z
z
)
k
z
X
p
m
n
(
k
k
)
{\displaystyle \mathbf {M} _{pmn}^{(3)}(k,\mathbf {r} )={\frac {i^{-n}}{2\pi k}}\iint _{-\infty }^{\infty }dk_{\|}{\frac {e^{i\left(k_{x}x+k_{y}y\pm k_{z}z\right)}}{k_{z}}}\mathbf {X} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)}
N
p
m
n
(
3
)
(
k
,
r
)
=
i
−
n
2
π
k
∬
−
∞
∞
d
k
‖
e
i
(
k
x
x
+
k
y
y
±
k
z
z
)
k
z
Z
p
m
n
(
k
k
)
{\displaystyle \mathbf {N} _{pmn}^{(3)}(k,\mathbf {r} )={\frac {i^{-n}}{2\pi k}}\iint _{-\infty }^{\infty }dk_{\|}{\frac {e^{i\left(k_{x}x+k_{y}y\pm k_{z}z\right)}}{k_{z}}}\mathbf {Z} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)}
k
z
=
k
2
−
k
x
2
−
k
y
2
{\textstyle k_{z}={\sqrt {k^{2}-k_{x}^{2}-k_{y}^{2}}}}
(
3
)
{\displaystyle (3)}
^ Barrera, R G; Estevez, G A; Giraldo, J (1985-10-01). "Vector spherical harmonics and their application to magnetostatics". European Journal of Physics . 6 (4). IOP Publishing: 287–294. Bibcode :1985EJPh....6..287B . CiteSeerX 10.1.1.718.2001 doi :10.1088/0143-0807/6/4/014 . ISSN 0143-0807 . S2CID 250894245 . ^ Carrascal, B; Estevez, G A; Lee, Peilian; Lorenzo, V (1991-07-01). "Vector spherical harmonics and their application to classical electrodynamics". European Journal of Physics . 12 (4). IOP Publishing: 184–191. Bibcode :1991EJPh...12..184C . doi :10.1088/0143-0807/12/4/007 . ISSN 0143-0807 . S2CID 250886412 . ^ Hill, E. L. (1954). "The Theory of Vector Spherical Harmonics" (PDF) . American Journal of Physics . 22 (4). American Association of Physics Teachers (AAPT): 211–214. Bibcode :1954AmJPh..22..211H . doi :10.1119/1.1933682 . ISSN 0002-9505 . S2CID 124182424 . Archived from the original (PDF) on 2020-04-12. ^ Weinberg, Erick J. (1994-01-15). "Monopole vector spherical harmonics". Physical Review D . 49 (2). American Physical Society (APS): 1086–1092. arXiv :hep-th/9308054 Bibcode :1994PhRvD..49.1086W . doi :10.1103/physrevd.49.1086 . ISSN 0556-2821 . PMID 10017069 . S2CID 6429605 . ^ P.M. Morse and H. Feshbach, Methods of Theoretical Physics, Part II , New York: McGraw-Hill, 1898-1901 (1953)
^ Bohren, Craig F. and Donald R. Huffman, Absorption and scattering of light by small particles, New York : Wiley, 1998, 530 p., ISBN 0-471-29340-7 , ISBN 978-0-471-29340-8 (second edition)
^ a b Stratton, J. A. (1941). Electromagnetic Theory ^ D. A. Varhalovich, A. N. Moskalev, and V. K. Khersonskii, Quantum Theory of Angular Momentum [in Russian], Nauka, Leningrad (1975)
^ Zhang, Huayong; Han, Yiping (2008). "Addition theorem for the spherical vector wave functions and its application to the beam shape coefficients". J. Opt. Soc. Am. B . 25 (2): 255–260. Bibcode :2008JOSAB..25..255Z . doi :10.1364/JOSAB.25.000255 . ^ Stein, Seymour (1961). "Addition theorems for spherical wave functions". Quarterly of Applied Mathematics . 19 (1): 15–24. doi :10.1090/qam/120407 . ^ a b Stout, B. (2012). Popov, E (ed.). "Spherical harmonic lattice sums for gratings" (PDF) . Institut Fresnel, Universite d'Aix-Marseille 6. Gratings: theory and numeric applications. ^ Wittmann, R. C. (1988). "Spherical wave operators and the translation formulas" . IEEE Transactions on Antennas and Propagation . 36 (8): 1078–1087. Bibcode :1988ITAP...36.1078W . doi :10.1109/8.7220 . 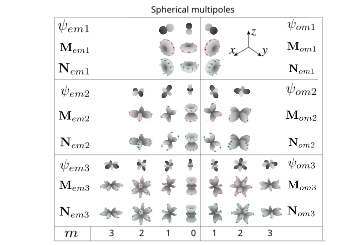






































































![{\displaystyle {\begin{aligned}{\mathbf {N} _{emn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\cos(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }}\\{{}+\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{{}-m\sin(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8331b5c5a9b7381413a4230f6dd294ea6e29ddca)
![{\displaystyle {\begin{aligned}\mathbf {N} _{omn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\sin(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }\\{}+\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{}+{m\cos(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d56063fb7f9fabaf20e04730bd1eeaf79296847)


![{\displaystyle {\begin{aligned}\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {L} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}k^{2}\left\{n\left[z_{n-1}(kr)\right]^{2}+(n+1)\left[z_{n+1}(kr)\right]^{2}\right\}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {M} _{^{e}_{o}mn}\cdot \mathbf {M} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{2n+1}}{\frac {(n+m)!}{(n-m)!}}n(n+1)\left[z_{n}(kr)\right]^{2}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {N} _{^{e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}n(n+1)\left\{(n+1)\left[z_{n-1}(kr)\right]^{2}+n\left[z_{n+1}(kr)\right]^{2}\right\}\\[3pt]\int _{0}^{\pi }\int _{0}^{2\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}n(n+1)k\left\{\left[z_{n-1}(kr)\right]^{2}-\left[z_{n+1}(kr)\right]^{2}\right\}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f3423865810fc65f5eb7bc80cfd88e8c9c9f16b)
![{\displaystyle {\hat {D}}(\alpha ,\beta ,\gamma )\mathbf {Y} _{JM}^{(s)}(\theta ,\varphi )=\sum _{M'=-J}^{J}[D_{MM'}^{(J)}(\alpha ,\beta ,\gamma )]^{*}\mathbf {Y} _{JM'}^{(s)}(\theta ,\varphi ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95badc97e00d533b5a7ba1dba9d762bfb9bcaca2)















