Window function
In signal processing and statistics, a window function (also known as an apodization function or tapering function[1]) is a mathematical function that is zero-valued outside of some chosen interval. Typically, window functions are symmetric around the middle of the interval, approach a maximum in the middle, and taper away from the middle. Mathematically, when another function or waveform/data-sequence is "multiplied" by a window function, the product is also zero-valued outside the interval: all that is left is the part where they overlap, the "view through the window". Equivalently, and in actual practice, the segment of data within the window is first isolated, and then only that data is multiplied by the window function values. Thus, tapering, not segmentation, is the main purpose of window functions.
The reasons for examining segments of a longer function include detection of transient events and time-averaging of frequency spectra. The duration of the segments is determined in each application by requirements like time and frequency resolution. But that method also changes the frequency content of the signal by an effect called spectral leakage. Window functions allow us to distribute the leakage spectrally in different ways, according to the needs of the particular application. There are many choices detailed in this article, but many of the differences are so subtle as to be insignificant in practice.
In typical applications, the window functions used are non-negative, smooth, "bell-shaped" curves.[2] Rectangle, triangle, and other functions can also be used. A more general definition of window functions does not require them to be identically zero outside an interval, as long as the product of the window multiplied by its argument is square integrable, and, more specifically, that the function goes sufficiently rapidly toward zero.[3]
Applications[edit]
Window functions are used in spectral analysis/modification/resynthesis,[4] the design of finite impulse response filters, merging multiscale and multidimensional datasets,[5][6] as well as beamforming and antenna design.

Spectral analysis[edit]
The Fourier transform of the function cos(ωt) is zero, except at frequency ±ω. However, many other functions and waveforms do not have convenient closed-form transforms. Alternatively, one might be interested in their spectral content only during a certain time period.
In either case, the Fourier transform (or a similar transform) can be applied on one or more finite intervals of the waveform. In general, the transform is applied to the product of the waveform and a window function. Any window (including rectangular) affects the spectral estimate computed by this method.
Filter design[edit]
Windows are sometimes used in the design of digital filters, in particular to convert an "ideal" impulse response of infinite duration, such as a sinc function, to a finite impulse response (FIR) filter design. That is called the window method.[7][8][9]
Statistics and curve fitting[edit]
Window functions are sometimes used in the field of statistical analysis to restrict the set of data being analyzed to a range near a given point, with a weighting factor that diminishes the effect of points farther away from the portion of the curve being fit. In the field of Bayesian analysis and curve fitting, this is often referred to as the kernel.
Rectangular window applications[edit]
Analysis of transients[edit]
When analyzing a transient signal in modal analysis, such as an impulse, a shock response, a sine burst, a chirp burst, or noise burst, where the energy vs time distribution is extremely uneven, the rectangular window may be most appropriate. For instance, when most of the energy is located at the beginning of the recording, a non-rectangular window attenuates most of the energy, degrading the signal-to-noise ratio.[10]
Harmonic analysis[edit]
One might wish to measure the harmonic content of a musical note from a particular instrument or the harmonic distortion of an amplifier at a given frequency. Referring again to Figure 2, we can observe that there is no leakage at a discrete set of harmonically-related frequencies sampled by the discrete Fourier transform (DFT). (The spectral nulls are actually zero-crossings, which cannot be shown on a logarithmic scale such as this.) This property is unique to the rectangular window, and it must be appropriately configured for the signal frequency, as described above.
Overlapping windows[edit]
When the length of a data set to be transformed is larger than necessary to provide the desired frequency resolution, a common practice is to subdivide it into smaller sets and window them individually. To mitigate the "loss" at the edges of the window, the individual sets may overlap in time. See Welch method of power spectral analysis and the modified discrete cosine transform.
Two-dimensional windows[edit]
Two-dimensional windows are commonly used in image processing to reduce unwanted high-frequencies in the image Fourier transform.[11] They can be constructed from one-dimensional windows in either of two forms.[12] The separable form, is trivial to compute. The radial form, , which involves the radius , is isotropic, independent on the orientation of the coordinate axes. Only the Gaussian function is both separable and isotropic.[13] The separable forms of all other window functions have corners that depend on the choice of the coordinate axes. The isotropy/anisotropy of a two-dimensional window function is shared by its two-dimensional Fourier transform. The difference between the separable and radial forms is akin to the result of diffraction from rectangular vs. circular apertures, which can be visualized in terms of the product of two sinc functions vs. an Airy function, respectively.
Examples of window functions[edit]
Conventions:
- is a zero-phase function (symmetrical about ),[14] continuous for where is a positive integer (even or odd).[15]
- The sequence is symmetric, of length
- is DFT-symmetric, of length [A]
- The parameter B displayed on each spectral plot is the function's noise equivalent bandwidth metric, in units of DFT bins.[16]: p.56 eq.(16)
- See spectral leakage §§ Discrete-time signals and Some window metrics and Normalized frequency for understanding the use of "bins" for the x-axis in these plots.
The sparse sampling of a discrete-time Fourier transform (DTFT) such as the DFTs in Fig 2 only reveals the leakage into the DFT bins from a sinusoid whose frequency is also an integer DFT bin. The unseen sidelobes reveal the leakage to expect from sinusoids at other frequencies.[a] Therefore, when choosing a window function, it is usually important to sample the DTFT more densely (as we do throughout this section) and choose a window that suppresses the sidelobes to an acceptable level.
Rectangular window[edit]

The rectangular window (sometimes known as the boxcar or uniform or Dirichlet window or misleadingly as "no window" in some programs[18]) is the simplest window, equivalent to replacing all but N consecutive values of a data sequence by zeros, making the waveform suddenly turn on and off:
Other windows are designed to moderate these sudden changes, to reduce scalloping loss and improve dynamic range (described in § Spectral analysis).
The rectangular window is the 1st-order B-spline window as well as the 0th-power power-of-sine window.
The rectangular window provides the minimum mean square error estimate of the Discrete-time Fourier transform, at the cost of other issues discussed.
B-spline windows[edit]
B-spline windows can be obtained as k-fold convolutions of the rectangular window. They include the rectangular window itself (k = 1), the § Triangular window (k = 2) and the § Parzen window (k = 4).[19] Alternative definitions sample the appropriate normalized B-spline basis functions instead of convolving discrete-time windows. A kth-order B-spline basis function is a piece-wise polynomial function of degree k−1 that is obtained by k-fold self-convolution of the rectangular function.
Triangular window[edit]

Triangular windows are given by:
where L can be N,[20] N + 1,[16] [21][22] or N + 2.[23] The first one is also known as Bartlett window or Fejér window. All three definitions converge at large N.
The triangular window is the 2nd-order B-spline window. The L = N form can be seen as the convolution of two N⁄2-width rectangular windows. The Fourier transform of the result is the squared values of the transform of the half-width rectangular window.
Parzen window[edit]

Defining L ≜ N + 1, the Parzen window, also known as the de la Vallée Poussin window,[16] is the 4th-order B-spline window given by:

Other polynomial windows[edit]
Welch window[edit]
The Welch window consists of a single parabolic section:
The defining quadratic polynomial reaches a value of zero at the samples just outside the span of the window.
Sine window[edit]

The corresponding function is a cosine without the π/2 phase offset. So the sine window[24] is sometimes also called cosine window.[16] As it represents half a cycle of a sinusoidal function, it is also known variably as half-sine window[25] or half-cosine window.[26]
The autocorrelation of a sine window produces a function known as the Bohman window.[27]
Power-of-sine/cosine windows[edit]
These window functions have the form:[28]
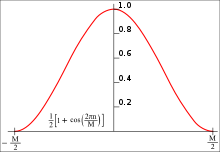
The rectangular window (α = 0), the sine window (α = 1), and the Hann window (α = 2) are members of this family.
For even-integer values of α these functions can also be expressed in cosine-sum form:
Cosine-sum windows[edit]
This family is also known as generalized cosine windows.
| (Eq.1) |
In most cases, including the examples below, all coefficients ak ≥ 0. These windows have only 2K + 1 non-zero N-point DFT coefficients.
Hann and Hamming windows[edit]


The customary cosine-sum windows for case K = 1 have the form:
which is easily (and often) confused with its zero-phase version:
Setting produces a Hann window:
named after Julius von Hann, and sometimes erroneously referred to as Hanning, presumably due to its linguistic and formulaic similarities to the Hamming window. It is also known as raised cosine, because the zero-phase version, is one lobe of an elevated cosine function.
This function is a member of both the cosine-sum and power-of-sine families. Unlike the Hamming window, the end points of the Hann window just touch zero. The resulting side-lobes roll off at about 18 dB per octave.[30]
Setting to approximately 0.54, or more precisely 25/46, produces the Hamming window, proposed by Richard W. Hamming. That choice places a zero-crossing at frequency 5π/(N − 1), which cancels the first sidelobe of the Hann window, giving it a height of about one-fifth that of the Hann window.[16][31][32] The Hamming window is often called the Hamming blip when used for pulse shaping.[33][34][35]
Approximation of the coefficients to two decimal places substantially lowers the level of sidelobes,[16] to a nearly equiripple condition.[32] In the equiripple sense, the optimal values for the coefficients are a0 = 0.53836 and a1 = 0.46164.[32][36]
Blackman window[edit]

Blackman windows are defined as:
By common convention, the unqualified term Blackman window refers to Blackman's "not very serious proposal" of α = 0.16 (a0 = 0.42, a1 = 0.5, a2 = 0.08), which closely approximates the exact Blackman,[37] with a0 = 7938/18608 ≈ 0.42659, a1 = 9240/18608 ≈ 0.49656, and a2 = 1430/18608 ≈ 0.076849.[38] These exact values place zeros at the third and fourth sidelobes,[16] but result in a discontinuity at the edges and a 6 dB/oct fall-off. The truncated coefficients do not null the sidelobes as well, but have an improved 18 dB/oct fall-off.[16][39]
Nuttall window, continuous first derivative[edit]

The continuous form of the Nuttall window, and its first derivative are continuous everywhere, like the Hann function. That is, the function goes to 0 at x = ±N/2, unlike the Blackman–Nuttall, Blackman–Harris, and Hamming windows. The Blackman window (α = 0.16) is also continuous with continuous derivative at the edge, but the "exact Blackman window" is not.
Blackman–Nuttall window[edit]

Blackman–Harris window[edit]

A generalization of the Hamming family, produced by adding more shifted sinc functions, meant to minimize side-lobe levels[40][41]
Flat top window[edit]

A flat top window is a partially negative-valued window that has minimal scalloping loss in the frequency domain. That property is desirable for the measurement of amplitudes of sinusoidal frequency components.[17][42] However, its broad bandwidth results in high noise bandwidth and wider frequency selection, which depending on the application could be a drawback.
Flat top windows can be designed using low-pass filter design methods,[42] or they may be of the usual cosine-sum variety:
The Matlab variant has these coefficients:
Other variations are available, such as sidelobes that roll off at the cost of higher values near the main lobe.[17]
Rife–Vincent windows[edit]
Rife–Vincent windows[43] are customarily scaled for unity average value, instead of unity peak value. The coefficient values below, applied to Eq.1, reflect that custom.
Class I, Order 1 (K = 1): Functionally equivalent to the Hann window.
Class I, Order 2 (K = 2):
Class I is defined by minimizing the high-order sidelobe amplitude. Coefficients for orders up to K=4 are tabulated.[44]
Class II minimizes the main-lobe width for a given maximum side-lobe.
Class III is a compromise for which order K = 2 resembles the § Blackman window.[44][45]
Adjustable windows[edit]
Gaussian window[edit]

The Fourier transform of a Gaussian is also a Gaussian. Since the support of a Gaussian function extends to infinity, it must either be truncated at the ends of the window, or itself windowed with another zero-ended window.[46]
Since the log of a Gaussian produces a parabola, this can be used for nearly exact quadratic interpolation in frequency estimation.[47][46][48]
The standard deviation of the Gaussian function is σ · N/2 sampling periods.

Confined Gaussian window[edit]
The confined Gaussian window yields the smallest possible root mean square frequency width σω for a given temporal width (N + 1) σt.[49] These windows optimize the RMS time-frequency bandwidth products. They are computed as the minimum eigenvectors of a parameter-dependent matrix. The confined Gaussian window family contains the § Sine window and the § Gaussian window in the limiting cases of large and small σt, respectively.

Approximate confined Gaussian window[edit]
Defining L ≜ N + 1, a confined Gaussian window of temporal width L × σt is well approximated by:[49]
where is a Gaussian function:
The standard deviation of the approximate window is asymptotically equal (i.e. large values of N) to L × σt for σt < 0.14.[49]
Generalized normal window[edit]
A more generalized version of the Gaussian window is the generalized normal window.[50] Retaining the notation from the Gaussian window above, we can represent this window as
for any even . At , this is a Gaussian window and as approaches , this approximates to a rectangular window. The Fourier transform of this window does not exist in a closed form for a general . However, it demonstrates the other benefits of being smooth, adjustable bandwidth. Like the § Tukey window, this window naturally offers a "flat top" to control the amplitude attenuation of a time-series (on which we don't have a control with Gaussian window). In essence, it offers a good (controllable) compromise, in terms of spectral leakage, frequency resolution and amplitude attenuation, between the Gaussian window and the rectangular window. See also [51] for a study on time-frequency representation of this window (or function).
Tukey window[edit]

The Tukey window, also known as the cosine-tapered window, can be regarded as a cosine lobe of width Nα/2 (spanning Nα/2 + 1 observations) that is convolved with a rectangular window of width N(1 − α/2).
At α = 0 it becomes rectangular, and at α = 1 it becomes a Hann window.
Planck-taper window[edit]

The so-called "Planck-taper" window is a bump function that has been widely used[53] in the theory of partitions of unity in manifolds. It is smooth (a function) everywhere, but is exactly zero outside of a compact region, exactly one over an interval within that region, and varies smoothly and monotonically between those limits. Its use as a window function in signal processing was first suggested in the context of gravitational-wave astronomy, inspired by the Planck distribution.[54] It is defined as a piecewise function:
The amount of tapering is controlled by the parameter ε, with smaller values giving sharper transitions.
DPSS or Slepian window[edit]
The DPSS (discrete prolate spheroidal sequence) or Slepian window maximizes the energy concentration in the main lobe,[55] and is used in multitaper spectral analysis, which averages out noise in the spectrum and reduces information loss at the edges of the window.
The main lobe ends at a frequency bin given by the parameter α.[56]
 |
 |
The Kaiser windows below are created by a simple approximation to the DPSS windows:
 |
 |
Kaiser window[edit]
The Kaiser, or Kaiser–Bessel, window is a simple approximation of the DPSS window using Bessel functions, discovered by James Kaiser.[57][58]
where is the 0th-order modified Bessel function of the first kind. Variable parameter determines the tradeoff between main lobe width and side lobe levels of the spectral leakage pattern. The main lobe width, in between the nulls, is given by in units of DFT bins,[65] and a typical value of is 3.
Dolph–Chebyshev window[edit]

Minimizes the Chebyshev norm of the side-lobes for a given main lobe width.[66]
The zero-phase Dolph–Chebyshev window function is usually defined in terms of its real-valued discrete Fourier transform, :[67]
Tn(x) is the n-th Chebyshev polynomial of the first kind evaluated in x, which can be computed using
and
is the unique positive real solution to , where the parameter α sets the Chebyshev norm of the sidelobes to −20α decibels.[66]
The window function can be calculated from W0(k) by an inverse discrete Fourier transform (DFT):[66]
The lagged version of the window can be obtained by:
which for even values of N must be computed as follows:
which is an inverse DFT of
Variations:
- Due to the equiripple condition, the time-domain window has discontinuities at the edges. An approximation that avoids them, by allowing the equiripples to drop off at the edges, is a Taylor window.
- An alternative to the inverse DFT definition is also available.[1].
Ultraspherical window[edit]

The Ultraspherical window was introduced in 1984 by Roy Streit[68] and has application in antenna array design,[69] non-recursive filter design,[68] and spectrum analysis.[70]
Like other adjustable windows, the Ultraspherical window has parameters that can be used to control its Fourier transform main-lobe width and relative side-lobe amplitude. Uncommon to other windows, it has an additional parameter which can be used to set the rate at which side-lobes decrease (or increase) in amplitude.[70][71][72]
The window can be expressed in the time-domain as follows:[70]
where is the Ultraspherical polynomial of degree N, and and control the side-lobe patterns.[70]
Certain specific values of yield other well-known windows: and give the Dolph–Chebyshev and Saramäki windows respectively.[68] See here for illustration of Ultraspherical windows with varied parametrization.
Exponential or Poisson window[edit]


The Poisson window, or more generically the exponential window increases exponentially towards the center of the window and decreases exponentially in the second half. Since the exponential function never reaches zero, the values of the window at its limits are non-zero (it can be seen as the multiplication of an exponential function by a rectangular window [73]). It is defined by
where τ is the time constant of the function. The exponential function decays as e ≃ 2.71828 or approximately 8.69 dB per time constant.[74] This means that for a targeted decay of D dB over half of the window length, the time constant τ is given by
Hybrid windows[edit]
Window functions have also been constructed as multiplicative or additive combinations of other windows.

Bartlett–Hann window[edit]
Planck–Bessel window[edit]

A § Planck-taper window multiplied by a Kaiser window which is defined in terms of a modified Bessel function. This hybrid window function was introduced to decrease the peak side-lobe level of the Planck-taper window while still exploiting its good asymptotic decay.[75] It has two tunable parameters, ε from the Planck-taper and α from the Kaiser window, so it can be adjusted to fit the requirements of a given signal.
Hann–Poisson window[edit]

A Hann window multiplied by a Poisson window. For it has no side-lobes, as its Fourier transform drops off forever away from the main lobe without local minima. It can thus be used in hill climbing algorithms like Newton's method.[76] The Hann–Poisson window is defined by:
where α is a parameter that controls the slope of the exponential.
Other windows[edit]

Generalized adaptive polynomial (GAP) window[edit]
The GAP window is a family of adjustable window functions that are based on a symmetrical polynomial expansion of order . It is continuous with continuous derivative everywhere. With the appropriate set of expansion coefficients and expansion order, the GAP window can mimic all the known window functions, reproducing accurately their spectral properties.
where is the standard deviation of the sequence.
Additionally, starting with a set of expansion coefficients that mimics a certain known window function, the GAP window can be optimized by minimization procedures to get a new set of coefficients that improve one or more spectral properties, such as the main lobe width, side lobe attenuation, and side lobe falloff rate.[78] Therefore, a GAP window function can be developed with designed spectral properties depending on the specific application.

Lanczos window[edit]
- used in Lanczos resampling
- for the Lanczos window, is defined as
- also known as a sinc window, because: is the main lobe of a normalized sinc function
Asymmetric window functions[edit]
The form, according to the convention above, is symmetric around . However, there are window functions that are asymmetric, such as the Gamma distribution used in FIR implementations of Gammatone filters. These asymmetries are used to reduce the delay when using large window sizes, or to emphasize the initial transient of a decaying pulse.[citation needed]
Any bounded function with compact support, including asymmetric ones, can be readily used as a window function. Additionally, there are ways to transform symmetric windows into asymmetric windows by transforming the time coordinate, such as with the below formula
where the window weights more highly the earliest samples when , and conversely weights more highly the latest samples when .[79]
See also[edit]
- Apodization
- Kolmogorov–Zurbenko filter
- Multitaper
- Short-time Fourier transform
- Spectral leakage
- Welch method
- Weight function
- Window design method
Notes[edit]
- ^ Some authors limit their attention to this important subset and to even values of N.[16][17] But the window coefficient formulas are still the ones presented here.
- ^ This formula can be confirmed by simplifying the cosine function at MATLAB tukeywin and substituting r=α and x=n/N.
- ^ Harris 1978 (p 67, eq 38) appears to have two errors: (1) The subtraction operator in the numerator of the cosine function should be addition. (2) The denominator contains a spurious factor of 2. Also, Fig 30 corresponds to α=0.25 using the Wikipedia formula, but to 0.75 using the Harris formula. Fig 32 is similarly mislabeled.
- ^ The Kaiser window is often parametrized by β, where β = πα.[59][60] [61][62][56][63][7]: p. 474 The alternative use of just α facilitates comparisons to the DPSS windows.[64]
Page citations[edit]
- ^ Harris 1978, p 57, fig 10.
References[edit]
- ^ Weisstein, Eric W. (2003). CRC Concise Encyclopedia of Mathematics. CRC Press. ISBN 978-1-58488-347-0.
- ^ Roads, Curtis (2002). Microsound. MIT Press. ISBN 978-0-262-18215-7.
- ^ Cattani, Carlo; Rushchitsky, Jeremiah (2007). Wavelet and Wave Analysis As Applied to Materials With Micro Or Nanostructure. World Scientific. ISBN 978-981-270-784-0.
- ^
"Overlap-Add (OLA) STFT Processing | Spectral Audio Signal Processing". www.dsprelated.com. Retrieved 2016-08-07.
The window is applied twice: once before the FFT (the "analysis window") and secondly after the inverse FFT prior to reconstruction by overlap-add (the so-called "synthesis window"). ... More generally, any positive COLA window can be split into an analysis and synthesis window pair by taking its square root.
- ^ Ajala, R.; Persaud, P. (2022). "Ground-Motion Evaluation of Hybrid Seismic Velocity Models". The Seismic Record. 2 (3): 186–196. doi:10.1785/0320220022. S2CID 251504921.
- ^ Ajala, R.; Persaud, P. (2021). "Effect of Merging Multiscale Models on Seismic Wavefield Predictions Near the Southern San Andreas Fault". Journal of Geophysical Research: Solid Earth. 126 (10). doi:10.1029/2021JB021915. ISSN 2169-9313. S2CID 239654900.
- ^ a b Oppenheim, Alan V.; Schafer, Ronald W.; Buck, John R. (1999). "7.2". Discrete-time signal processing (2nd ed.). Upper Saddle River, N.J.: Prentice Hall. pp. 465–478. ISBN 0-13-754920-2.
- ^ "FIR Filters by Windowing – The Lab Book Pages". www.labbookpages.co.uk. Retrieved 2016-04-13.
- ^ "Mastering Windows" (PDF). www.cg.tuwien.ac.at. Retrieved 2020-02-12.
- ^ "The Fundamentals of Signal Analysis Application Note 243" (PDF). hpmemoryproject.org. Retrieved 10 April 2018.
- ^
R. Hovden, Y. Jiang, H. Xin, L.F. Kourkoutis (2015). "Periodic Artifact Reduction in Fourier Transforms of Full Field Atomic Resolution Images". Microscopy and Microanalysis. 21 (2): 436–441. arXiv:2210.09024. Bibcode:2015MiMic..21..436H. doi:10.1017/S1431927614014639. PMID 25597865. S2CID 22435248.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Bernstein, Matt A.; King, Kevin Franklin; Zhou, Xiaohong Joe (2004). Handbook of MRI Pulse Sequences. London: Elsevier Academic Press. pp. 495–499. ISBN 0-12-092861-2.
- ^ Awad, A.I.; Baba, K. (2011). "An Application for Singular Point Location in Fingerprint Classification". Digital Information Processing and Communications. Communications in Computer and Information Science. Vol. 188. p. 262. doi:10.1007/978-3-642-22389-1_24. ISBN 978-3-642-22388-4.
- ^ "Zero Phase Filters". ccrma.stanford.edu. Retrieved 2020-02-12.
- ^ Rorabaugh, C.Britton (October 1998). DSP Primer. Primer series. McGraw-Hill Professional. p. 196. ISBN 978-0-07-054004-0.
- ^ a b c d e f g h i j Harris, Fredric J. (Jan 1978). "On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform" (PDF). Proceedings of the IEEE. 66 (1): 51–83. Bibcode:1978IEEEP..66...51H. CiteSeerX 10.1.1.649.9880. doi:10.1109/PROC.1978.10837. S2CID 426548. The fundamental 1978 paper on FFT windows by Harris, which specified many windows and introduced key metrics used to compare them.
- ^ a b c Heinzel, G.; Rüdiger, A.; Schilling, R. (2002). Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new flat-top windows (Technical report). Max Planck Institute (MPI) für Gravitationsphysik / Laser Interferometry & Gravitational Wave Astronomy. 395068.0. Retrieved 2013-02-10. Also available at https://pure.mpg.de/rest/items/item_152164_1/component/file_152163/content
- ^ "Understanding FFTs and Windowing" (PDF). National Instruments. Archived (PDF) from the original on 2024-01-05. Retrieved 2024-02-13.
- ^ Toraichi, K.; Kamada, M.; Itahashi, S.; Mori, R. (1989). "Window functions represented by B-spline functions". IEEE Transactions on Acoustics, Speech, and Signal Processing. 37: 145–147. doi:10.1109/29.17517.
- ^ "Bartlett Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ Tukey, J.W. (1967). "An introduction to the calculations of numerical spectrum analysis". Spectral Analysis of Time Series: 25–46.
- ^ "Triangular window – MATLAB triang". www.mathworks.com. Retrieved 2016-04-13.
- ^ a b Welch, P. (1967). "The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms". IEEE Transactions on Audio and Electroacoustics. 15 (2): 70–73. Bibcode:1967ITAE...15...70W. doi:10.1109/TAU.1967.1161901. S2CID 13900622.
- ^ Bosi, Marina; Goldberg, Richard E. (2003). "Time to Frequency Mapping Part II: The MDCT". Introduction to Digital Audio Coding and Standards. The Springer International Series in Engineering and Computer Science. Vol. 721. Boston, MA: Springer US. p. 106. doi:10.1007/978-1-4615-0327-9. ISBN 978-1-4615-0327-9.
- ^ Kido, Ken'iti; Suzuki, Hideo; Ono, Takahiko; Fukushima, Manabu (1998). "Deformation of impulse response estimates by time window in cross spectral technique". Journal of the Acoustical Society of Japan (E). 19 (5): 349–361. doi:10.1250/ast.19.349.
- ^ Landisman, M.; Dziewonski, A.; Satô, Y. (1969-05-01). "Recent Improvements in the Analysis of Surface Wave Observations". Geophysical Journal International. 17 (4): 369–403. Bibcode:1969GeoJ...17..369L. doi:10.1111/j.1365-246X.1969.tb00246.x.
- ^ "Bohman window – R2019B". www.mathworks.com. Retrieved 2020-02-12.
- ^ "Power-of-Cosine Window Family". ccrma.stanford.edu. Retrieved 10 April 2018.
- ^ "Hann (Hanning) window - MATLAB hann". www.mathworks.com. Retrieved 2020-02-12.
- ^ "Hann or Hanning or Raised Cosine". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ Enochson, Loren D.; Otnes, Robert K. (1968). Programming and Analysis for Digital Time Series Data. U.S. Dept. of Defense, Shock and Vibration Info. Center. p. 142.
- ^ a b c "Hamming Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ "A digital quadrature amplitude modulation (QAM) Radio: Building a better radio" (PDF). users.wpi.edu. p. 28. Retrieved 2020-02-12.
- ^ "Bits to Symbols to Signals and back again" (PDF). users.wpi.edu. p. 7. Retrieved 2020-02-12.
- ^ Johnson, C.Richard Jr; Sethares, William A.; Klein, Andrew G. (2011-08-18). "11". Software Receiver Design. Cambridge University Press. ISBN 978-1-139-50145-3. Also https://cnx.org/contents/QsVBJjB4@3.1:6R_ztzDY@4/Pulse-Shaping-and-Receive-Filtering
- ^ Nuttall, Albert H. (Feb 1981). "Some Windows with Very Good Sidelobe Behavior". IEEE Transactions on Acoustics, Speech, and Signal Processing. 29 (1): 84–91. doi:10.1109/TASSP.1981.1163506. Extends Harris' paper, covering all the window functions known at the time, along with key metric comparisons.
- ^ Weisstein, Eric W. "Blackman Function". mathworld.wolfram.com. Retrieved 2016-04-13.
- ^ "Characteristics of Different Smoothing Windows - NI LabVIEW 8.6 Help". zone.ni.com. Retrieved 2020-02-13.
- ^ Blackman, R.B.; Tukey, J.W. (1959-01-01). The Measurement of Power Spectra from the Point of View of Communications Engineering. Dover Publications. p. 99. ISBN 978-0-486-60507-4.
- ^ "Blackman-Harris Window Family". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ "Three-Term Blackman-Harris Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ a b Smith, Steven W. (2011). The Scientist and Engineer's Guide to Digital Signal Processing. San Diego, California, USA: California Technical Publishing. Retrieved 2013-02-14.
- ^ Rife, David C.; Vincent, G.A. (1970), "Use of the discrete Fourier transform in the measurement of frequencies and levels of tones", Bell Syst. Tech. J., 49 (2): 197–228, doi:10.1002/j.1538-7305.1970.tb01766.x
- ^ a b Andria, Gregorio; Savino, Mario; Trotta, Amerigo (1989), "Windows and interpolation algorithms to improve electrical measurement accuracy", IEEE Transactions on Instrumentation and Measurement, 38 (4): 856–863, Bibcode:1989ITIM...38..856A, doi:10.1109/19.31004
- ^ Schoukens, Joannes; Pintelon, Rik; Van Hamme, Hugo (1992), "The interpolated fast Fourier transform: a comparative study", IEEE Transactions on Instrumentation and Measurement, 41 (2): 226–232, Bibcode:1992ITIM...41..226S, doi:10.1109/19.137352
- ^ a b
"Matlab for the Gaussian Window". ccrma.stanford.edu. Retrieved 2016-04-13.
Note that, on a dB scale, Gaussians are quadratic. This means that parabolic interpolation of a sampled Gaussian transform is exact. ... quadratic interpolation of spectral peaks may be more accurate on a log-magnitude scale (e.g., dB) than on a linear magnitude scale
- ^ "Gaussian Window and Transform". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ "Quadratic Interpolation of Spectral Peaks". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ a b c Starosielec, S.; Hägele, D. (2014). "Discrete-time windows with minimal RMS bandwidth for given RMS temporal width". Signal Processing. 102: 240–246. doi:10.1016/j.sigpro.2014.03.033.
- ^ Chakraborty, Debejyo; Kovvali, Narayan (2013). "Generalized normal window for digital signal processing". 2013 IEEE International Conference on Acoustics, Speech and Signal Processing. pp. 6083–6087. doi:10.1109/ICASSP.2013.6638833. ISBN 978-1-4799-0356-6. S2CID 11779529.
- ^ Diethorn, E.J. (1994). "The generalized exponential time-frequency distribution". IEEE Transactions on Signal Processing. 42 (5): 1028–1037. Bibcode:1994ITSP...42.1028D. doi:10.1109/78.295214.
- ^ Bloomfield, P. (2000). Fourier Analysis of Time Series: An Introduction. New York: Wiley-Interscience.
- ^ Tu, Loring W. (2008). "Bump Functions and Partitions of Unity". An Introduction to Manifolds. Universitext. New York: Springer. pp. 127–134. doi:10.1007/978-0-387-48101-2_13. ISBN 978-0-387-48098-5.
- ^ McKechan, D.J.A.; Robinson, C.; Sathyaprakash, B.S. (21 April 2010). "A tapering window for time-domain templates and simulated signals in the detection of gravitational waves from coalescing compact binaries". Classical and Quantum Gravity. 27 (8): 084020. arXiv:1003.2939. Bibcode:2010CQGra..27h4020M. doi:10.1088/0264-9381/27/8/084020. S2CID 21488253.
- ^ "Slepian or DPSS Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ a b Smith, J.O. (2011). "Kaiser and DPSS Windows Compared". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^
Kaiser, James F.; Kuo, Franklin F. (1966). System Analysis by Digital Computer. John Wiley and Sons. pp. 232–235.
This family of window functions was "discovered" by Kaiser in 1962 following a discussion with B. F. Logan of the Bell Telephone Laboratories. ... Another valuable property of this family ... is that they also approximate closely the prolate spheroidal wave functions of order zero.
- ^ Kaiser, James F. (Nov 1964). "A family of window functions having nearly ideal properties". Unpublished Memorandum.
- ^ Rabiner, Lawrence R.; Gold, Bernard (1975). "3.11". Theory and application of digital signal processing. Englewood Cliffs, N.J.: Prentice-Hall. p. 94. ISBN 0-13-914101-4.
- ^ Crochiere, R.E.; Rabiner, L.R. (1983). "4.3.1". Multirate Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall. p. 144. ISBN 0-13-605162-6.
- ^ Lin, Yuan-Pei; Vaidyanathan, P.P. (June 1998). "A Kaiser Window Approach for the Design of Prototype Filters of Cosine Modulated Filterbanks" (PDF). IEEE Signal Processing Letters. 5 (6): 132–134. Bibcode:1998ISPL....5..132L. doi:10.1109/97.681427. S2CID 18159105. Retrieved 2017-03-16.
- ^
Smith, J.O. (2011). "Kaiser Window". ccrma.stanford.edu. Retrieved 2019-03-20.
Sometimes the Kaiser window is parametrized by α, where β = πα.
- ^ "Kaiser Window, R2020a". www.mathworks.com. Mathworks. Retrieved 9 April 2020.
- ^
"Kaiser Window". www.dsprelated.com. Retrieved 2020-04-08.
The following Matlab comparison of the DPSS and Kaiser windows illustrates the interpretation of α as the bin number of the edge of the critically sampled window main lobe.
- ^ Kaiser, James F.; Schafer, Ronald W. (1980). "On the use of the I0-sinh window for spectrum analysis". IEEE Transactions on Acoustics, Speech, and Signal Processing. 28: 105–107. doi:10.1109/TASSP.1980.1163349.
- ^ a b c "Dolph-Chebyshev Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ "Dolph-Chebyshev Window Definition". ccrma.stanford.edu. Retrieved 2019-03-05.
- ^ a b c Kabal, Peter (2009). "Time Windows for Linear Prediction of Speech" (PDF). Technical Report, Dept. Elec. & Comp. Eng., McGill University (2a): 31. Retrieved 2 February 2014.
- ^ Streit, Roy (1984). "A two-parameter family of weights for nonrecursive digital filters and antennas". Transactions of ASSP. 32: 108–118. doi:10.1109/tassp.1984.1164275.
- ^ a b c d Deczky, Andrew (2001). "Unispherical Windows". ISCAS 2001. The 2001 IEEE International Symposium on Circuits and Systems (Cat. No. 01CH37196). Vol. 2. pp. 85–88. doi:10.1109/iscas.2001.921012. ISBN 978-0-7803-6685-5. S2CID 38275201.
- ^ Bergen, S.W.A.; Antoniou, A. (2004). "Design of Ultraspherical Window Functions with Prescribed Spectral Characteristics". EURASIP Journal on Applied Signal Processing. 2004 (13): 2053–2065. Bibcode:2004EJASP2004...63B. doi:10.1155/S1110865704403114.
- ^ Bergen, Stuart W. A. (2005). "Design of the Ultraspherical Window Function and Its Applications" (PDF). Dissertation, University of Viktoria.
- ^ Smith, Julius O. III (2011-04-23). "Poisson Window". ccrma.stanford.edu. Retrieved 2020-02-12.
- ^ Gade, Svend; Herlufsen, Henrik (1987). "Technical Review No 3-1987: Windows to FFT analysis (Part I)" (PDF). Brüel & Kjær. Retrieved 2011-11-22.
- ^ Berry, C.P.L.; Gair, J.R. (12 December 2012). "Observing the Galaxy's massive black hole with gravitational wave bursts". Monthly Notices of the Royal Astronomical Society. 429 (1): 589–612. arXiv:1210.2778. Bibcode:2013MNRAS.429..589B. doi:10.1093/mnras/sts360. S2CID 118944979.
- ^ "Hann-Poisson Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ Wesley Beccaro (2020-10-31), "Generalized Adaptive Polynomial Window Function", mathworks.com, retrieved 2020-11-02
- ^ "Generalized Adaptive Polynomial Window Function". www.mathworks.com. Retrieved 2020-12-12.
- ^ Luo, Jiufel; Xie, Zhijiang; Li, Xinyi (2015-03-02). "Asymmetric Windows and Their Application in Frequency Estimation". Chongqing University. 9 (Algorithms & Computational Technology): 389–412. doi:10.1260/1748-3018.9.4.389. S2CID 124464194.
Further reading[edit]
- Harris, Frederic J. (September 1976). "Windows, Harmonic Analysis, and the Discrete Fourier Transform" (PDF). apps.dtic.mil. Naval Undersea Center, San Diego. Archived (PDF) from the original on April 8, 2019. Retrieved 2019-04-08.
- Albrecht, Hans-Helge (2012). Tailored minimum sidelobe and minimum sidelobe cosine-sum windows. Version 1.0. Vol. ISBN 978-3-86918-281-0 ). editor: Physikalisch-Technische Bundesanstalt. Physikalisch-Technische Bundesanstalt. doi:10.7795/110.20121022aa. ISBN 978-3-86918-281-0.
- Bergen, S.W.A.; Antoniou, A. (2005). "Design of Nonrecursive Digital Filters Using the Ultraspherical Window Function". EURASIP Journal on Applied Signal Processing. 2005 (12): 1910–1922. Bibcode:2005EJASP2005...44B. doi:10.1155/ASP.2005.1910.
- Prabhu, K. M. M. (2014). Window Functions and Their Applications in Signal Processing. Boca Raton, FL: CRC Press. ISBN 978-1-4665-1583-3.
- US patent 7065150, Park, Young-Seo, "System and method for generating a root raised cosine orthogonal frequency division multiplexing (RRC OFDM) modulation", published 2003, issued 2006
External links[edit]
 Media related to Window function at Wikimedia Commons
Media related to Window function at Wikimedia Commons- LabView Help, Characteristics of Smoothing Filters, http://zone.ni.com/reference/en-XX/help/371361B-01/lvanlsconcepts/char_smoothing_windows/
- Creation and properties of Cosine-sum Window functions, http://electronicsart.weebly.com/fftwindows.html
- Online Interactive FFT, Windows, Resolution, and Leakage Simulation | RITEC | Library & Tools






![{\displaystyle x\in [-N/2,N/2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0377d29e5715ebdd13819c1cc07c4638a0156afd)

![{\displaystyle \{w[n]=w_{0}(n-N/2),\quad 0\leq n\leq N\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f28eb10c2426fe0deb507ce933eb6b5df2c020e)

![{\displaystyle \{w[n],\quad 0\leq n\leq N-1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f506d61ded38a4f9d8ecd59004fbf34e793d81f3)

![{\displaystyle w[n]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f071fdd6a0a02d6d9dc3c1325d88a6dda6a92781)
![{\displaystyle w[n]=1-\left|{\frac {n-{\frac {N}{2}}}{\frac {L}{2}}}\right|,\quad 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884ef77423e593a74ebf40ec3eaa0c8f00ca5102)

![{\displaystyle w[n]=\ w_{0}\left(n-{\tfrac {N}{2}}\right),\ 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfa5797bd28cc542de9f224e4b9c7c0c37bff91a)
![{\displaystyle w[n]=1-\left({\frac {n-{\frac {N}{2}}}{\frac {N}{2}}}\right)^{2},\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3a944c6a5c2051217a53dd60a9693dd76c98a9)
![{\displaystyle w[n]=\sin \left({\frac {\pi n}{N}}\right)=\cos \left({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2af9f7febc105f1184bd114a1484bf16cf7325)

![{\displaystyle w[n]=\sin ^{\alpha }\left({\frac {\pi n}{N}}\right)=\cos ^{\alpha }\left({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b81af4c85e4b5e6909b3dfb7fef170a42a02f7e)
![{\displaystyle w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)-a_{3}\cos \left({\frac {6\pi n}{N}}\right)+a_{4}\cos \left({\frac {8\pi n}{N}}\right)-...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3449e818cb0c7c261fe536655c3b5145fd4eda9d)

![{\displaystyle w[n]=\sum _{k=0}^{K}(-1)^{k}a_{k}\;\cos \left({\frac {2\pi kn}{N}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e597f0587d0c29feaf791fef475cf419be2987c9)
![{\displaystyle w[n]=a_{0}-\underbrace {(1-a_{0})} _{a_{1}}\cdot \cos \left({\tfrac {2\pi n}{N}}\right),\quad 0\leq n\leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72b8f8c3192b06191db2bb7ad9247eeba6a6cb70)
![{\displaystyle {\begin{aligned}w_{0}(n)\ &=w\left[n+{\tfrac {N}{2}}\right]\\&=a_{0}+a_{1}\cdot \cos \left({\tfrac {2\pi n}{N}}\right),\quad -{\tfrac {N}{2}}\leq n\leq {\tfrac {N}{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a04d79e8c4de591b5badfd2864ebe7522c17b1ad)

![{\displaystyle w[n]=0.5\;\left[1-\cos \left({\frac {2\pi n}{N}}\right)\right]=\sin ^{2}\left({\frac {\pi n}{N}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd8d3e844a1443d7bedd57240588cf19fcd28af1)


![{\displaystyle w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e1a6c47fc77da0b81229c3234068706a6ca8e6a)


![{\displaystyle w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)-a_{3}\cos \left({\frac {6\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55aa618bd5010d83e5df4ae06fbb3abd509f12fd)



![{\displaystyle {\begin{aligned}w[n]=a_{0}&{}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)\\&{}-a_{3}\cos \left({\frac {6\pi n}{N}}\right)+a_{4}\cos \left({\frac {8\pi n}{N}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e117d087bf8d6345fb6ea8ffc7b5aa7f6faae4a)



![{\displaystyle w[n]=\exp \left(-{\frac {1}{2}}\left({\frac {n-N/2}{\sigma N/2}}\right)^{2}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e201c829f6aabf4339fc0a1929367d5613dfe290)

![{\displaystyle w[n]=G(n)-{\frac {G(-{\tfrac {1}{2}})[G(n+L)+G(n-L)]}{G(-{\tfrac {1}{2}}+L)+G(-{\tfrac {1}{2}}-L)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3094fa9469d1e65bfdb6a4e31cdafd037a8822ec)


![{\displaystyle w[n,p]=\exp \left(-\left({\frac {n-N/2}{\sigma N/2}}\right)^{p}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/704a7de7c2a67fc8a24a140a151491bd7362698c)



![{\displaystyle \left.{\begin{array}{lll}w[n]={\frac {1}{2}}\left[1-\cos \left({\frac {2\pi n}{\alpha N}}\right)\right],\quad &0\leq n<{\frac {\alpha N}{2}}\\w[n]=1,\quad &{\frac {\alpha N}{2}}\leq n\leq {\frac {N}{2}}\\w[N-n]=w[n],\quad &0\leq n\leq {\frac {N}{2}}\end{array}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab34271ac62f34c531c4d6cc0b8ffd2e9793623a)

![{\displaystyle \left.{\begin{array}{lll}w[0]=0,\\w[n]=\left(1+\exp \left({\frac {\varepsilon N}{n}}-{\frac {\varepsilon N}{\varepsilon N-n}}\right)\right)^{-1},\quad &1\leq n<\varepsilon N\\w[n]=1,\quad &\varepsilon N\leq n\leq {\frac {N}{2}}\\w[N-n]=w[n],\quad &0\leq n\leq {\frac {N}{2}}\end{array}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f50bb4690593ab87a47ed71fec1945a3f95b9d0d)
![{\displaystyle w[n]={\frac {I_{0}\left(\pi \alpha {\sqrt {1-\left({\frac {2n}{N}}-1\right)^{2}}}\right)}{I_{0}(\pi \alpha )}},\quad 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337ca65bf1465649348a8eb22356662c4188b092)




![{\displaystyle w_{0}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0d68356ad0cc45bf520fbe5be3266aa7c431cd8)
![{\displaystyle W_{0}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af1b9baa4526ac8ec5f39c3cd63782248015037f)





![{\displaystyle w[n]=w_{0}\left(n-{\frac {N}{2}}\right),\quad 0\leq n\leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3af173b60d19716e14882dabdec080868fa3e0ae)
![{\displaystyle {\begin{aligned}w_{0}\left(n-{\frac {N}{2}}\right)={\frac {1}{N+1}}\sum _{k=0}^{N}W_{0}(k)\cdot e^{\frac {i2\pi k(n-N/2)}{N+1}}={\frac {1}{N+1}}\sum _{k=0}^{N}\left[\left(-e^{\frac {i\pi }{N+1}}\right)^{k}\cdot W_{0}(k)\right]e^{\frac {i2\pi kn}{N+1}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f3590133d3da32b13aa211153542e96d14a46e)

![{\displaystyle w[n]={\frac {1}{N+1}}\left[C_{N}^{\mu }(x_{0})+\sum _{k=1}^{\frac {N}{2}}C_{N}^{\mu }\left(x_{0}\cos {\frac {k\pi }{N+1}}\right)\cos {\frac {2n\pi k}{N+1}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe5e8dc43d2c5edbe601e3abf542a177689f4276)





![{\displaystyle w[n]=e^{-\left|n-{\frac {N}{2}}\right|{\frac {1}{\tau }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/141d1630d759c1ebf5120671e36f86a6117f259c)

![{\displaystyle w[n]=a_{0}-a_{1}\left|{\frac {n}{N}}-{\frac {1}{2}}\right|-a_{2}\cos \left({\frac {2\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e64d33f0c717a2b40af2ed16c9fff5f58d95b937)


![{\displaystyle w[n]={\frac {1}{2}}\left(1-\cos \left({\frac {2\pi n}{N}}\right)\right)e^{\frac {-\alpha \left|N-2n\right|}{N}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e7d44df8e90604b099629079cb1ed07faa045a3)

![{\displaystyle w_{0}[n]=a_{0}+\sum _{k=1}^{K}a_{2k}\left({\frac {n}{\sigma }}\right)^{2k},\quad -{\frac {N}{2}}\leq n\leq {\frac {N}{2}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0985efd235d3dcfbd7c9a2631aa173cd5c2d4cdf)



![{\displaystyle w[n]=\operatorname {sinc} \left({\frac {2n}{N}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/380ec565d5a93c55eb9d1109065556115b5c0f99)





