Main sequence: Difference between revisions
→Formation: Also needs to lose excess energy. |
→Structure: Increase in luminosity as the star evolves. |
||
| Line 98: | Line 98: | ||
All main sequence stars have a convection zone. In massive stars, the core region is unstable to convection and the material undergoes mixing. This removes the helium ashes from the hydrogen burning region, allowing more of the hydrogen in the star to be burned. The outer regions of a massive star transport energy by radiation, with little or no convection. Medium-sized stars like the Sun have a core region that is stable against convection and a convection zone near the surface. This produces mixing of the outer layers, but a less efficient burning of the hydrogen in the star. The eventual result is the buildup of a helium-rich core, surrounded by a hydrogen-rich region. By contrast, cool, low-mass stars are convective throughout. The helium produced at the core is distributed across the star, producing a relatively uniform atmosphere.<ref name=brainerd/> |
All main sequence stars have a convection zone. In massive stars, the core region is unstable to convection and the material undergoes mixing. This removes the helium ashes from the hydrogen burning region, allowing more of the hydrogen in the star to be burned. The outer regions of a massive star transport energy by radiation, with little or no convection. Medium-sized stars like the Sun have a core region that is stable against convection and a convection zone near the surface. This produces mixing of the outer layers, but a less efficient burning of the hydrogen in the star. The eventual result is the buildup of a helium-rich core, surrounded by a hydrogen-rich region. By contrast, cool, low-mass stars are convective throughout. The helium produced at the core is distributed across the star, producing a relatively uniform atmosphere.<ref name=brainerd/> |
||
As non-fusing helium ash accumulates in the core, the reduction in the abundance of hydrogen per unit mass results in a gradual lowering of the fusion rate within that mass. To compensate, the core temperature and pressure slowly increase, which actually causes a net increase in the overall fusion rate (to support the greater density of the inner star). This causes a steady increase in the luminosity and radius of the star over time. Thus, for example, the luminosity of the early Sun was only about 70% of its current value.<ref>{{cite journal |
|||
| last=Gough | first=D. O. |
|||
| title=Solar interior structure and luminosity variations |
|||
| journal=Solar Physics | year=1981 | volume=74 | pages=21-34 |
|||
| url=http://adsabs.harvard.edu/abs/1981SoPh...74...21G |
|||
| accessdate=2007-12-06 }}</ref> The luminosity increase of a star changes its position on the HR diagram; resulting in a broadening of the main sequence band because stars are observed at random stages in their lifetime.<ref>{{cite book |
|||
| first=Thanu | last=Padmanabhan | year=2001 |
|||
| title=Theoretical Astrophysics |
|||
| publisher=Cambridge University Press |
|||
| id=ISBN 0521562414 }}</ref> |
|||
===Lifetime=== |
===Lifetime=== |
||
Revision as of 17:14, 5 December 2007

The main sequence is the name for a continuous sequence of stars that appear on a plot of color versus brightness for groups of stars. These color-magnitude plots are known as Hertzsprung-Russell diagrams after their co-developers, Ejnar Hertzsprung and Henry Norris Russell. Stars on this band are known as main-sequence stars or dwarf stars.
History
In the early part of the twentieth century, information about the types and distances of stars became more readily available. The spectra of stars were show to have distinctive features, which allowed them to be categorized. Annie Jump Cannon and Edward C. Pickering at Harvard College Observatory had developed a method of categorization that became known as the Harvard classification scheme. This scheme was published in the Harvard Annals in 1901.[1]
In Potsdam in 1906, the Danish astronomer Ejnar Hertzsprung noticed that the reddest stars, classified as K and M in the Harvard scheme, could be divided into two distinct groups. These stars are either much brighter than the Sun, or much fainter. To distinguish these groups, he called them "giant" and "dwarf" stars. The following year he began studying star clusters; large groupings of stars that are co-located at approximately the same distance. He published the first plots of color versus luminosity for these stars.These plots showed a prominent and continuous sequence of stars, which he named the main sequence.[2]
At Princeton University, Henry Norris Russell was following a similar course of research. He was studying the relationship between the spectral classification of stars and their actual brightness as corrected for distance—their absolute magnitude. For this purpose he used a set of stars that had reliable parallaxes and many of which had been categorized at Harvard. When he plotted the spectral stypes of these stars against their absolute magnitude, he found that dwarf stars followed a distinct relationship. This allowed the real brightness of a dwarf star to be predicted with reasonable accuracy.[3]
Of the red stars observed by Hertzsprung, the dwarf stars also followed the spectra-luminosity relationship discovered by Russell. However, the giant stars are much brighter than dwarfs and so do not follow the same relatiohship. Russell proposed that the giant stars must have a lower density or higher surface-brightness than dwarfs. The same curve also showed that there were very few faint white stars.[3]
In 1933, Elis Strömgren introduced the term Hertzsprung-Russel diagram to denote a luminosity-spectral class diagram. This name reflected the parallel development of this technique by both Hertzsprung and Russell earlier in the century.[2]
As evolutionary models of stars were developed during the 1930s, it was shown that, for stars of a uniform chemical composition, a relationship exists between a star's mass and its luminosity and radius. That is, for a given mass and composition is known, there is a unique solution determining the star's radius and luminosity. This became known as the Vogt-Russell theorem; named after Heinrich Vogt and Henry Norris Russell. By this theorem, once a star's chemical composition and its position on the main sequence is known, so too is the star's mass and radius. (However, tt was subsequently discovered that the theorem breaks down somewhat for stars of non-uniform composition.)[4]
A refined scheme for stellar classification was published in 1943 by W. W. Morgan and P. C. Keenan.[5] The MK classification assigned each star a spectral type—based on the Harvard classification—and a luminosity class. For historical reasons, the spectral types of stars followed, with colors ranging from blue to red, the sequence O, B, A, F, G, K and M. The luminosity class ranged from I to V, in order of decreasing luminosity. Stars of luminosity class V belonged to the main sequence.[6]
Characteristics
Formation
When a protostar is formed from the collapse of a giant molecular cloud of gas and dust, the initial composition is homogeneous throughout, consisting of about 70% hydrogen, 28% helium and trace amounts of other elements, by mass. During the initial collapse, this pre-main sequence star generates energy through gravitational contraction. Upon reaching a suitable density, energy generation is begun at the core using an exothermic nuclear fusion process that converts hydrogen into helium.[6]
Once nuclear fusion of hydrogen becomes the dominant energy production process and the excess energy gained from gravitational contraction has been lost,[7] the star lies along a curve on the Hertzsprung-Russell diagram (or HR diagram) called the standard main sequence. The star remains near its initial position on this line until a significant amount of hydrogen in the core has been consumed, then begins to evolve into a more luminous star. (On the HR diagram, the evolving star moves up and to the right of the main sequence.) Thus the main sequence represents the primary hydrogen-burning stage of a star's lifetime.[6]
The majority of stars on a typical HR diagram lie along the main sequence curve. This line is so pronounced because both the spectral type and the luminosity depend only on a star's mass, at least to zeroth order approximation, as long as it is fusing hydrogen—and that is what almost all stars spend most of their "active" life doing.[8] These main-sequence (and therefore "normal") stars are called dwarf stars. This is not because they are unusually small, but instead they have smaller radii and are less luminous than the other main type of stars, the giant stars.[9] White dwarfs are a different kind of star which are smaller than main sequence stars—roughly the size of the Earth. These represent the final evolutionary stage of many main sequence stars.[10]
Astronomers will sometimes refer to the "zero age main sequence", or ZAMS. This is a line calculated by computer models of where a star will be when it begins hydrogen fusion; its brightness and surface temperature typically increase from this point with age. Stars usually enter and leave the main sequence from about when they are born or when they are starting to die, respectively.
Structure
All main sequence stars have a core region where energy is generated by nuclear fusion. The temperature and density of this core are at the levels necessary to sustain the energy production needed to support the remainder of the star. A reduction of energy production would cause the overlaying mass to compress, increasing the temperature and pressure needed for fusion. Likewise an increase in energy production would cause the star to expand, lowering the pressure at the core. Thus the star forms a self-regulating system in hydrostatic equilibrium that is stable over the course of its main sequence lifetime.[11]
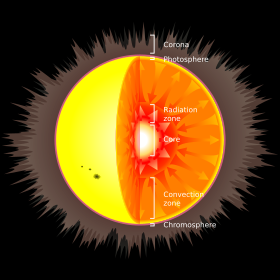
Because there is a temperature difference between the core and the surface, or photosphere, energy is transported outward. The two modes for transporting this energy are radiation and convection. A radiation zone, where energy is transported by radiation, is stable against convection and there is very little mixing of the plasma. By contrast, in a convection zone, energy is transported by bulk movement of plasma, with the hotter material rising and cooler material descending. Convection is a more efficient mode for carrying energy than radiation, but it will only occur under conditions that create a steep temperature gradient.[12][11]
All main sequence stars have a convection zone. In massive stars, the core region is unstable to convection and the material undergoes mixing. This removes the helium ashes from the hydrogen burning region, allowing more of the hydrogen in the star to be burned. The outer regions of a massive star transport energy by radiation, with little or no convection. Medium-sized stars like the Sun have a core region that is stable against convection and a convection zone near the surface. This produces mixing of the outer layers, but a less efficient burning of the hydrogen in the star. The eventual result is the buildup of a helium-rich core, surrounded by a hydrogen-rich region. By contrast, cool, low-mass stars are convective throughout. The helium produced at the core is distributed across the star, producing a relatively uniform atmosphere.[11]
As non-fusing helium ash accumulates in the core, the reduction in the abundance of hydrogen per unit mass results in a gradual lowering of the fusion rate within that mass. To compensate, the core temperature and pressure slowly increase, which actually causes a net increase in the overall fusion rate (to support the greater density of the inner star). This causes a steady increase in the luminosity and radius of the star over time. Thus, for example, the luminosity of the early Sun was only about 70% of its current value.[13] The luminosity increase of a star changes its position on the HR diagram; resulting in a broadening of the main sequence band because stars are observed at random stages in their lifetime.[14]
Lifetime
The lifespan that a star spends on the main sequence is governed by two factors. The total amount of energy that can be generated through nuclear fusion of hydrogen is limited by the amount of available hydrogen fuel that can be consumed at the core. For a star in equilibrium, the energy generated at the core must be at least equal to the energy radiated at the surface. Since the luminosity gives the amount of energy radiated per unit time, the total life span can be estimated, to first approximation, as the total energy produced divided by the star's luminosity.[15]
Our Sun is a main sequence star—it has been one for about 4.5 billion years and will continue to be one for another 5.5 billion years, for a total main sequence lifetime of 1010 years. After the hydrogen supply in the core is exhausted, it will expand to become a red giant and fuse helium atoms to form carbon. As the energy output of the helium fusion process per unit mass is only about a tenth the energy output of the hydrogen process, this stage will only last for about 10% of a star's total active lifetime. Thus, on average, about 90% of the observed stars will be on the main sequence.[16]
On average, main sequence stars are known to follow an empirical mass-luminosity relationship. The luminosity (L) of the star is approximately related to the total mass (M) as the following power law:
The amount of fuel available for nuclear fusion is proportional to the mass of the star. Thus, the lifetime of a star on the main sequence can be estimated by comparing it to the Sun:[17]
where is the mass of the Sun, is the mass of the star and is the star's estimated main sequence lifetime in years.
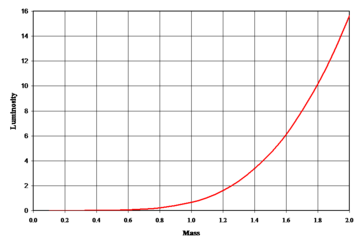
This is a counter-intuitive result, as more massive stars have more fuel to burn and might be expected to last longer. Instead, the lightest stars, of less than a tenth of a solar mass, may last over a trillion years.[18] For the heaviest stars, however, this mass-luminosity relationship poorly matches the estimated lifetime, which last at least a few million years. A more accurate representation gives a different function for various ranges of mass.
The mass-luminosity relationship depends on how efficiently energy can be transported from the core to the surface. A higher opacity has an insulating effect that retains more energy at the core, so the star doesn't need to produce as much energy to remain in hydrostatic equilibrium. By contrast, a lower opacity means energy escapes more rapidly and the star must burn more fuel to remain in equilibrium. Note, however, that a sufficiently high opacity can result in energy transport via convection, which changes the conditions needed to remain in equilibrium.
In high mass main sequence stars, the opacity is dominated by electron scattering, which is nearly constant with increasing temperature. Thus the luminosity only increases as the cube of the star's mass.[19] For stars below 10 times the mass of the Sun, the opacity becomes dependent on temperature, resulting in the luminosity varying approximately as the fourth power of the star's mass.[20] For very low mass stars, molecules in the atmosphere also contribute to the opacity. Below about 0.5 solar masses, the luminosity of the star varies as the mass to the power of 2.3, producing a flattening of the slope on a graph of mass versus luminosity. Even these refinements are only an approximation, however, and the mass-luminosity relation can vary depending on a stars composition.[21]
Metallicity
The main sequence does not follow a completely even curve; this is primarily because of the observational uncertainties which mainly affect the distance of the star in question but range all the way to unresolved binary stars.
However, even perfect observations would lead to a fuzzy main sequence, because mass is not a star's only parameter. Chemical composition and—related—its evolutionary status also move a star slightly on the main sequence, as do close companions, rotation, or magnetic fields, to name just a few factors. Actually, there are very metal-poor stars (subdwarfs) that lie just below the main sequence although they are fusing hydrogen, thus marking the lower edge of the main sequence's fuzziness due to chemical composition.
Stellar parameters
The table below shows typical values for stars along the main sequence. The values of luminosity (L), radius (R) and mass (M) are relative to the Sun—a dwarf star with a spectral classification of G2 V. The actual values for a star may vary by as much as 20-30% from the values listed below. The coloration of the stellar class column gives an approximate representation of the star's photographic color, which is a function of the surface temperaure. A popular mnemonic for memorizing the sequence of stellar classes is "Oh Be A Fine Girl/Guy, Kiss Me".
Stellar
ClassRadius Mass Luminosity Temperature Example R/R☉ M/M☉ L/L☉ K O2 16 158 2,000,000 54,000 Sanduleak −71° 51 O5 14 58 800,000 46,000 Sanduleak −66° 41 B0 5.7 16 16,000 29,000 Phi1 Orionis B5 3.7 5.4 750 15,200 Pi Andromedae A A0 2.3 2.6 63 9,600 Vega A5 1.8 1.9 24 8,700 Beta Pictoris F0 1.5 1.6 9.0 7,200 Gamma Virginis F5 1.2 1.35 4.0 6,400 Eta Arietis G0 1.05 1.08 1.45 6,000 Beta Comae Berenices G2 1.0 1.0 1.0 5,700 Sun G5 0.98 0.95 0.70 5,500 Alpha Mensae K0 0.89 0.83 0.36 5,150 70 Ophiuchi A K5 0.75 0.62 0.18 4,450 61 Cygni A M0 0.64 0.47 0.075 3,850 Gliese 185 M5 0.36 0.25 0.013 3,200 EZ Aquarii A M8 0.15 0.10 0.0008 2,500 Van Biesbroeck's star M9.5 0.10 0.08 0.0001 1,900 LP 647-013
See also
References
- ^ Longair, Malcolm S. (2006). The Cosmic Century: A History of Astrophysics and Cosmology. Cambridge University Press. ISBN 0521474361.
- ^ a b Brown, Laurie M. (1995). Twentieth Century Physics. CRC Press. ISBN 0750303107.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ a b Russell, H. N. (1913). ""Giant" and "dwarf" stars". The Observatory. 36: 324–329. Retrieved 2007-12-02.
- ^ Schatzman, Evry L. (1993). The Stars. Springer. ISBN 3540541969.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Morgan, W. W. (1943). An atlas of stellar spectra, with an outline of spectral classification. Chicago, Illinois: The University of Chicago press.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ a b c Unsöld, Albrecht (1969). The New Cosmos. Springer-Verlag New York Inc. pp. p. 268.
{{cite book}}:|pages=has extra text (help) - ^ Schilling, Govert (2001). "New Model Shows Sun Was a Hot Young Star". Science. 293 (5538): 2188–2189. Retrieved 2007-02-04.
- ^ "Main Sequence Stars". Australia Telescope Outreach and Education. Retrieved 2007-12-04.
- ^ Moore, Patrick (2006). The Amateur Astronomer. Springer. ISBN 1852338784.
- ^ "White Dwarf". COSMOS—The SAO Encyclopedia of Astronomy. Swinburne University. Retrieved 2007-12-04.
- ^ a b c Brainerd, Jim (February 16, 2005). "Main-Sequence Stars". The Astrophysics Spectator. Retrieved 2007-12-04.
{{cite web}}: Check date values in:|date=(help) - ^ Aller, Lawrence H. (1991). Atoms, Stars, and Nebulae. Cambridge University Press. ISBN 0521310407.
- ^ Gough, D. O. (1981). "Solar interior structure and luminosity variations". Solar Physics. 74: 21–34. Retrieved 2007-12-06.
- ^ Padmanabhan, Thanu (2001). Theoretical Astrophysics. Cambridge University Press. ISBN 0521562414.
- ^ Richmond, Michael (November 10, 2004). "Stellar evolution on the main sequence". Rochester Institute of Technology. Retrieved 2007-12-03.
{{cite web}}: Check date values in:|date=(help) - ^ Arnett, David (1996). Supernovae and Nucleosynthesis: An Investigation of the History of Matter, from the Big Bang to the Present. Princeton University Press. ISBN 0691011478.—Hydrogen fusion produces 8×1018 erg/g while helium fusion produces 8×1017 erg/g.
- ^ Richmond, Michael. "Stellar evolution on the main sequence". Retrieved 2006-08-24.
- ^ Laughlin, Gregory (1997). "The End of the Main Sequence". The Astrophysical Journal. 482: 420–432. Retrieved 2007-02-04.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Prialnik, Dina (2000). An Introduction to the Theory of Stellar Structure and Evolution. Cambridge UniversityPress. ISBN 052165937X.
- ^ Rolfs, Claus E. (1988). Cauldrons in the Cosmos: Nuclear Astrophysics. University of Chicago Press. ISBN 0226724573.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Kroupa, Pavel (2002). "The Initial Mass Function of Stars: Evidence for Uniformity in Variable Systems". Science. 295 (5552): 82–91. Retrieved 2007-12-03.


![{\displaystyle {\begin{smallmatrix}\tau _{ms}\ \sim \ 10^{10}{\text{years}}\cdot \left[{\frac {M}{M_{\bigodot }}}\right]\cdot \left[{\frac {L_{\bigodot }}{L}}\right]\ =\ 10^{10}{\text{years}}\cdot \left[{\frac {M_{\bigodot }}{M}}\right]^{2.5}\end{smallmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/917aab555d7c0fc087e16a4c7fc7081d06d462d0)


