Eb/N0
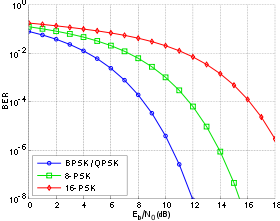
In digital communication or data transmission, (energy per bit to noise power spectral density ratio) is a normalized signal-to-noise ratio (SNR) measure, also known as the "SNR per bit". It is especially useful when comparing the bit error rate (BER) performance of different digital modulation schemes without taking bandwidth into account.
As the description implies, is the signal energy associated with each user data bit; it is equal to the signal power divided by the user bit rate (not the channel symbol rate). If signal power is in watts and bit rate is in bits per second, is in units of joules (watt-seconds). is the noise spectral density, the noise power in a 1 Hz bandwidth, measured in watts per hertz or joules.
These are the same units as so the ratio is dimensionless; it is frequently expressed in decibels. directly indicates the power efficiency of the system without regard to modulation type, error correction coding or signal bandwidth (including any use of spread spectrum). This also avoids any confusion as to which of several definitions of "bandwidth" to apply to the signal.
But when the signal bandwidth is well defined, is also equal to the signal-to-noise ratio (SNR) in that bandwidth divided by the "gross" link spectral efficiency in bit/s⋅Hz, where the bits in this context again refer to user data bits, irrespective of error correction information and modulation type.[1]
must be used with care on interference-limited channels since additive white noise (with constant noise density ) is assumed, and interference is not always noise-like. In spread spectrum systems (e.g., CDMA), the interference is sufficiently noise-like that it can be represented as and added to the thermal noise to produce the overall ratio .
Relation to carrier-to-noise ratio[edit]
is closely related to the carrier-to-noise ratio (CNR or ), i.e. the signal-to-noise ratio (SNR) of the received signal, after the receiver filter but before detection:
where
is the channel data rate (net bit rate) and
B is the channel bandwidth.
The equivalent expression in logarithmic form (dB):
Caution: Sometimes, the noise power is denoted by when negative frequencies and complex-valued equivalent baseband signals are considered rather than passband signals, and in that case, there will be a 3 dB difference.
Relation to Es/N0[edit]
can be seen as a normalized measure of the energy per symbol to noise power spectral density ():
where is the energy per symbol in joules and ρ is the nominal spectral efficiency in (bits/s)/Hz.[2] is also commonly used in the analysis of digital modulation schemes. The two quotients are related to each other according to the following:
where M is the number of alternative modulation symbols, e.g. for QPSK and for 8PSK.
This is the energy per bit, not the energy per information bit.
can further be expressed as:
where
is the carrier-to-noise ratio or signal-to-noise ratio,
B is the channel bandwidth in hertz, and
is the symbol rate in baud or symbols per second.
Shannon limit[edit]
The Shannon–Hartley theorem says that the limit of reliable information rate (data rate exclusive of error-correcting codes) of a channel depends on bandwidth and signal-to-noise ratio according to:
where
I is the information rate in bits per second excluding error-correcting codes,
B is the bandwidth of the channel in hertz,
S is the total signal power (equivalent to the carrier power C), and
N is the total noise power in the bandwidth.
This equation can be used to establish a bound on for any system that achieves reliable communication, by considering a gross bit rate R equal to the net bit rate I and therefore an average energy per bit of , with noise spectral density of . For this calculation, it is conventional to define a normalized rate , a bandwidth utilization parameter of bits per second per half hertz, or bits per dimension (a signal of bandwidth B can be encoded with dimensions, according to the Nyquist–Shannon sampling theorem). Making appropriate substitutions, the Shannon limit is:
Which can be solved to get the Shannon-limit bound on :
When the data rate is small compared to the bandwidth, so that is near zero, the bound, sometimes called the ultimate Shannon limit,[3] is:
which corresponds to −1.59 dB.
This often-quoted limit of −1.59 dB applies only to the theoretical case of infinite bandwidth. The Shannon limit for finite-bandwidth signals is always higher.
Cutoff rate[edit]
For any given system of coding and decoding, there exists what is known as a cutoff rate , typically corresponding to an about 2 dB above the Shannon capacity limit. [citation needed]The cutoff rate used to be thought of as the limit on practical error correction codes without an unbounded increase in processing complexity, but has been rendered largely obsolete by the more recent discovery of turbo codes, low-density parity-check (LDPC) and polar codes.
References[edit]
- ^ Chris Heegard and Stephen B. Wicker (1999). Turbo coding. Kluwer. p. 3. ISBN 978-0-7923-8378-9.
- ^ Forney, David. "MIT OpenCourseWare, 6.451 Principles of Digital Communication II, Lecture Notes section 4.2" (PDF). Retrieved 8 November 2017.
- ^ Nevio Benvenuto and Giovanni Cherubini (2002). Algorithms for Communications Systems and Their Applications. John Wiley & Sons. p. 508. ISBN 0-470-84389-6.
External links[edit]
- Eb/N0 Explained. An introductory article on




























