Faber–Jackson relation
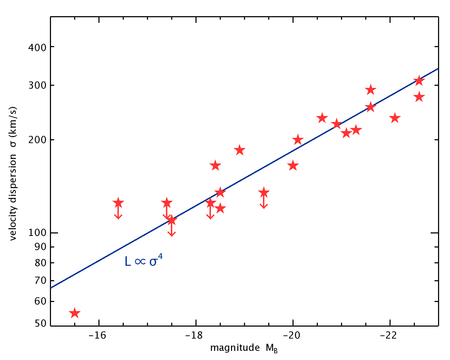
The Faber–Jackson relation provided the first empirical power-law relation between the luminosity and the central stellar velocity dispersion of elliptical galaxy, and was presented by the astronomers Sandra M. Faber and Robert Earl Jackson in 1976. Their relation can be expressed mathematically as:
with the index approximately equal to 4.
In 1962, Rudolph Minkowski had discovered and wrote that a "correlation between velocity dispersion and [luminosity] exists, but it is poor" and that "it seems important to extend the observations to more objects, especially at low and medium absolute magnitudes".[1] This was important because the value of depends on the range of galaxy luminosities that is fitted, with a value of 2 for low-luminosity elliptical galaxies discovered by a team led by Roger Davies,[2] and a value of 5 reported by Paul L. Schechter for luminous elliptical galaxies.[3]
The Faber–Jackson relation is understood as a projection of the fundamental plane of elliptical galaxies. One of its main uses is as a tool for determining distances to external galaxies.
Theory[edit]
The gravitational potential of a mass distribution of radius and mass is given by the expression:
Where α is a constant depending e.g. on the density profile of the system and G is the gravitational constant. For a constant density,
The kinetic energy is:
(Recall is the 1-dimensional velocity dispersion. Therefore, .) From the virial theorem ( ) it follows
If we assume that the mass to light ratio, , is constant, e.g. we can use this and the above expression to obtain a relation between and :
Let us introduce the surface brightness, and assume this is a constant (which from a fundamental theoretical point of view, is a totally unjustified assumption) to get
Using this and combining it with the relation between and , this results in
and by rewriting the above expression, we finally obtain the relation between luminosity and velocity dispersion:
that is
Given that massive galaxies originate from homologous merging, and the fainter ones from dissipation, the assumption of constant surface brightness can no longer be supported. Empirically, surface brightness exhibits a peak at about . The revised relation then becomes
for the less massive galaxies, and
for the more massive ones. With these revised formulae, the fundamental plane splits into two planes inclined by about 11 degrees to each other.
Even first-ranked cluster galaxies do not have constant surface brightness. A claim supporting constant surface brightness was presented by astronomer Allan R. Sandage in 1972 based on three logical arguments and his own empirical data. In 1975, Donald Gudehus showed that each of the logical arguments was incorrect and that first-ranked cluster galaxies exhibited a standard deviation of about half a magnitude.
Estimating distances to galaxies[edit]
Like the Tully–Fisher relation, the Faber–Jackson relation provides a means of estimating the distance to a galaxy, which is otherwise hard to obtain, by relating it to more easily observable properties of the galaxy. In the case of elliptical galaxies, if one can measure the central stellar velocity dispersion, which can be done relatively easily by using spectroscopy to measure the Doppler shift of light emitted by the stars, then one can obtain an estimate of the true luminosity of the galaxy via the Faber–Jackson relation. This can be compared to the apparent magnitude of the galaxy, which provides an estimate of the distance modulus and, hence, the distance to the galaxy.
By combining a galaxy's central velocity dispersion with measurements of its central surface brightness and radius parameter, it is possible to improve the estimate of the galaxy's distance even more. This standard yardstick, or "reduced galaxian radius-parameter", , devised by Gudehus in 1991, can yield distances, free of systematic bias, accurate to about 31%.
See also[edit]
References[edit]
- ^ Minkowski, R. (1962), Internal Dispersion of Velocities in Other Galaxies
- ^ Davies, R. L.; Efstathiou, G.; Fall, S. M.; Illingworth, G.; Schechter, P. L. (1983), The kinematic properties of faint elliptical galaxies
- ^ Paul L. Schechter (1980), Mass-to-light ratios for elliptical galaxies

























