Logical connective
| Logical connectives | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||
| Related concepts | ||||||||||||||||||||||
| Applications | ||||||||||||||||||||||
|
| ||||||||||||||||||||||
In logic, a logical connective (also called a logical operator, sentential connective, or sentential operator) is a logical constant. Connectives can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary connective can be used to join the two atomic formulas and , rendering the complex formula .
Common connectives include negation, disjunction, conjunction, implication, and equivalence. In standard systems of classical logic, these connectives are interpreted as truth functions, though they receive a variety of alternative interpretations in nonclassical logics. Their classical interpretations are similar to the meanings of natural language expressions such as English "not", "or", "and", and "if", but not identical. Discrepancies between natural language connectives and those of classical logic have motivated nonclassical approaches to natural language meaning as well as approaches which pair a classical compositional semantics with a robust pragmatics.
A logical connective is similar to, but not equivalent to, a syntax commonly used in programming languages called a conditional operator.[1][better source needed]
Overview
[edit]In formal languages, truth functions are represented by unambiguous symbols. This allows logical statements to not be understood in an ambiguous way. These symbols are called logical connectives, logical operators, propositional operators, or, in classical logic, truth-functional connectives. For the rules which allow new well-formed formulas to be constructed by joining other well-formed formulas using truth-functional connectives, see well-formed formula.
Logical connectives can be used to link zero or more statements, so one can speak about n-ary logical connectives. The boolean constants True and False can be thought of as zero-ary operators. Negation is a 1-ary connective, and so on.
| Symbol, name | Truth table |
Venn diagram | ||||||
|---|---|---|---|---|---|---|---|---|
| Zeroary connectives (constants) | ||||||||
| ⊤ | Truth/tautology | 1 | ||||||
| ⊥ | Falsity/contradiction | 0 | ||||||
| Unary connectives | ||||||||
| = | 0 | 1 | ||||||
| Proposition | 0 | 1 | ||||||
| ¬ | Negation | 1 | 0 | |||||
| Binary connectives | ||||||||
| = | 0 | 0 | 1 | 1 | ||||
| = | 0 | 1 | 0 | 1 | ||||
| Proposition | 0 | 0 | 1 | 1 | ||||
| Proposition | 0 | 1 | 0 | 1 | ||||
| ∧ | Conjunction | 0 | 0 | 0 | 1 | |||
| ↑ | Alternative denial | 1 | 1 | 1 | 0 | |||
| ∨ | Disjunction | 0 | 1 | 1 | 1 | |||
| ↓ | Joint denial | 1 | 0 | 0 | 0 | |||
| → | Material conditional | 1 | 1 | 0 | 1 | |||
| Exclusive or | 0 | 1 | 1 | 0 | ||||
| ↔ | Biconditional | 1 | 0 | 0 | 1 | |||
| ← | Converse implication | 1 | 0 | 1 | 1 | |||
| More information | ||||||||
List of common logical connectives
[edit]Commonly used logical connectives include the following ones.[2]
- Negation (not): , , (prefix) in which is the most modern and widely used, and is used by many people too;
- Conjunction (and): , , (prefix) in which is the most modern and widely used;
- Disjunction (or): , (prefix) in which is the most modern and widely used;
- Implication (if...then): , , , (prefix) in which is the most modern and widely used, and is used by many people too;
- Equivalence (if and only if): , , , , (prefix) in which is the most modern and widely used, and may be also a good choice compared to denoting implication just like to .
For example, the meaning of the statements it is raining (denoted by ) and I am indoors (denoted by ) is transformed, when the two are combined with logical connectives:
- It is not raining ();
- It is raining and I am indoors ();
- It is raining or I am indoors ();
- If it is raining, then I am indoors ();
- If I am indoors, then it is raining ();
- I am indoors if and only if it is raining ().
It is also common to consider the always true formula and the always false formula to be connective (in which case they are nullary).
This table summarizes the terminology:
| Connective | In English | Noun for parts | Verb phrase |
|---|---|---|---|
| Conjunction | Both A and B | conjunct | A and B are conjoined |
| Disjunction | Either A or B, or both | disjunct | A and B are disjoined |
| Negation | It is not the case that A | negatum/negand | A is negated |
| Conditional | If A, then B | antecedent, consequent | B is implied by A |
| Biconditional | A if, and only if, B | equivalents | A and B are equivalent |
History of notations
[edit]- Negation: the symbol appeared in Heyting in 1930[3][4] (compare to Frege's symbol ⫟ in his Begriffsschrift[5]); the symbol appeared in Russell in 1908;[6] an alternative notation is to add a horizontal line on top of the formula, as in ; another alternative notation is to use a prime symbol as in .
- Conjunction: the symbol appeared in Heyting in 1930[3] (compare to Peano's use of the set-theoretic notation of intersection [7]); the symbol appeared at least in Schönfinkel in 1924;[8] the symbol comes from Boole's interpretation of logic as an elementary algebra.
- Disjunction: the symbol appeared in Russell in 1908[6] (compare to Peano's use of the set-theoretic notation of union ); the symbol is also used, in spite of the ambiguity coming from the fact that the of ordinary elementary algebra is an exclusive or when interpreted logically in a two-element ring; punctually in the history a together with a dot in the lower right corner has been used by Peirce.[9]
- Implication: the symbol appeared in Hilbert in 1918;[10]: 76 was used by Russell in 1908[6] (compare to Peano's Ɔ the inverted C); appeared in Bourbaki in 1954.[11]
- Equivalence: the symbol in Frege in 1879;[12] in Becker in 1933 (not the first time and for this see the following);[13] appeared in Bourbaki in 1954;[14] other symbols appeared punctually in the history, such as in Gentzen,[15] in Schönfinkel[8] or in Chazal, [16]
- True: the symbol comes from Boole's interpretation of logic as an elementary algebra over the two-element Boolean algebra; other notations include (abbreviation for the Latin word "verum") to be found in Peano in 1889.
- False: the symbol comes also from Boole's interpretation of logic as a ring; other notations include (rotated ) to be found in Peano in 1889.
Some authors used letters for connectives: for conjunction (German's "und" for "and") and for disjunction (German's "oder" for "or") in early works by Hilbert (1904);[17] for negation, for conjunction, for alternative denial, for disjunction, for implication, for biconditional in Łukasiewicz in 1929.
Redundancy
[edit]Such a logical connective as converse implication "" is actually the same as material conditional with swapped arguments; thus, the symbol for converse implication is redundant. In some logical calculi (notably, in classical logic), certain essentially different compound statements are logically equivalent. A less trivial example of a redundancy is the classical equivalence between and . Therefore, a classical-based logical system does not need the conditional operator "" if "" (not) and "" (or) are already in use, or may use the "" only as a syntactic sugar for a compound having one negation and one disjunction.
There are sixteen Boolean functions associating the input truth values and with four-digit binary outputs.[18] These correspond to possible choices of binary logical connectives for classical logic. Different implementations of classical logic can choose different functionally complete subsets of connectives.
One approach is to choose a minimal set, and define other connectives by some logical form, as in the example with the material conditional above. The following are the minimal functionally complete sets of operators in classical logic whose arities do not exceed 2:
- One element
- , .
- Two elements
- , , , , , , , , , , , , , , , , , .
- Three elements
- , , , , , .
Another approach is to use with equal rights connectives of a certain convenient and functionally complete, but not minimal set. This approach requires more propositional axioms, and each equivalence between logical forms must be either an axiom or provable as a theorem.
The situation, however, is more complicated in intuitionistic logic. Of its five connectives, {∧, ∨, →, ¬, ⊥}, only negation "¬" can be reduced to other connectives (see False (logic) § False, negation and contradiction for more). Neither conjunction, disjunction, nor material conditional has an equivalent form constructed from the other four logical connectives.
Natural language
[edit]The standard logical connectives of classical logic have rough equivalents in the grammars of natural languages. In English, as in many languages, such expressions are typically grammatical conjunctions. However, they can also take the form of complementizers, verb suffixes, and particles. The denotations of natural language connectives is a major topic of research in formal semantics, a field that studies the logical structure of natural languages.
The meanings of natural language connectives are not precisely identical to their nearest equivalents in classical logic. In particular, disjunction can receive an exclusive interpretation in many languages. Some researchers have taken this fact as evidence that natural language semantics is nonclassical. However, others maintain classical semantics by positing pragmatic accounts of exclusivity which create the illusion of nonclassicality. In such accounts, exclusivity is typically treated as a scalar implicature. Related puzzles involving disjunction include free choice inferences, Hurford's Constraint, and the contribution of disjunction in alternative questions.
Other apparent discrepancies between natural language and classical logic include the paradoxes of material implication, donkey anaphora and the problem of counterfactual conditionals. These phenomena have been taken as motivation for identifying the denotations of natural language conditionals with logical operators including the strict conditional, the variably strict conditional, as well as various dynamic operators.
The following table shows the standard classically definable approximations for the English connectives.
| English word | Connective | Symbol | Logical gate |
|---|---|---|---|
| not | negation | NOT | |
| and | conjunction | AND | |
| or | disjunction | OR | |
| if...then | material implication | IMPLY | |
| ...if | converse implication | ||
| either...or | exclusive disjunction | XOR | |
| if and only if | biconditional | XNOR | |
| not both | alternative denial | NAND | |
| neither...nor | joint denial | NOR | |
| but not | material nonimplication | NIMPLY |
Properties
[edit]Some logical connectives possess properties that may be expressed in the theorems containing the connective. Some of those properties that a logical connective may have are:
- Associativity
- Within an expression containing two or more of the same associative connectives in a row, the order of the operations does not matter as long as the sequence of the operands is not changed.
- Commutativity
- The operands of the connective may be swapped, preserving logical equivalence to the original expression.
- Distributivity
- A connective denoted by · distributes over another connective denoted by +, if a · (b + c) = (a · b) + (a · c) for all operands a, b, c.
- Idempotence
- Whenever the operands of the operation are the same, the compound is logically equivalent to the operand.
- Absorption
- A pair of connectives ∧, ∨ satisfies the absorption law if for all operands a, b.
- Monotonicity
- If f(a1, ..., an) ≤ f(b1, ..., bn) for all a1, ..., an, b1, ..., bn ∈ {0,1} such that a1 ≤ b1, a2 ≤ b2, ..., an ≤ bn. E.g., ∨, ∧, ⊤, ⊥.
- Affinity
- Each variable always makes a difference in the truth-value of the operation or it never makes a difference. E.g., ¬, ↔, , ⊤, ⊥.
- Duality
- To read the truth-value assignments for the operation from top to bottom on its truth table is the same as taking the complement of reading the table of the same or another connective from bottom to top. Without resorting to truth tables it may be formulated as g̃(¬a1, ..., ¬an) = ¬g(a1, ..., an). E.g., ¬.
- Truth-preserving
- The compound all those arguments are tautologies is a tautology itself. E.g., ∨, ∧, ⊤, →, ↔, ⊂ (see validity).
- Falsehood-preserving
- The compound all those argument are contradictions is a contradiction itself. E.g., ∨, ∧, , ⊥, ⊄, ⊅ (see validity).
- Involutivity (for unary connectives)
- f(f(a)) = a. E.g. negation in classical logic.
For classical and intuitionistic logic, the "=" symbol means that corresponding implications "...→..." and "...←..." for logical compounds can be both proved as theorems, and the "≤" symbol means that "...→..." for logical compounds is a consequence of corresponding "...→..." connectives for propositional variables. Some many-valued logics may have incompatible definitions of equivalence and order (entailment).
Both conjunction and disjunction are associative, commutative and idempotent in classical logic, most varieties of many-valued logic and intuitionistic logic. The same is true about distributivity of conjunction over disjunction and disjunction over conjunction, as well as for the absorption law.
In classical logic and some varieties of many-valued logic, conjunction and disjunction are dual, and negation is self-dual, the latter is also self-dual in intuitionistic logic.
This section needs expansion. You can help by adding to it. (March 2012) |
Order of precedence
[edit]As a way of reducing the number of necessary parentheses, one may introduce precedence rules: ¬ has higher precedence than ∧, ∧ higher than ∨, and ∨ higher than →. So for example, is short for .
Here is a table that shows a commonly used precedence of logical operators.[19][20]
| Operator | Precedence |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 |
However, not all compilers use the same order; for instance, an ordering in which disjunction is lower precedence than implication or bi-implication has also been used.[21] Sometimes precedence between conjunction and disjunction is unspecified requiring to provide it explicitly in given formula with parentheses. The order of precedence determines which connective is the "main connective" when interpreting a non-atomic formula.
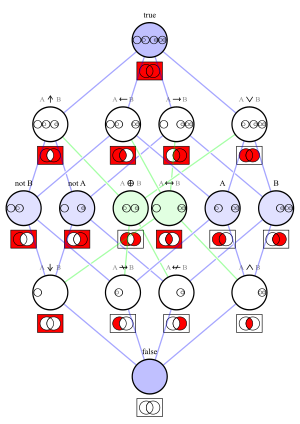
Table and Hasse diagram
[edit]The 16 logical connectives can be partially ordered to produce the following Hasse diagram. The partial order is defined by declaring that if and only if whenever holds then so does
 |
 | |
Applications
[edit]Logical connectives are used in computer science and in set theory.
Computer science
[edit]A truth-functional approach to logical operators is implemented as logic gates in digital circuits. Practically all digital circuits (the major exception is DRAM) are built up from NAND, NOR, NOT, and transmission gates; see more details in Truth function in computer science. Logical operators over bit vectors (corresponding to finite Boolean algebras) are bitwise operations.
But not every usage of a logical connective in computer programming has a Boolean semantic. For example, lazy evaluation is sometimes implemented for P ∧ Q and P ∨ Q, so these connectives are not commutative if either or both of the expressions P, Q have side effects. Also, a conditional, which in some sense corresponds to the material conditional connective, is essentially non-Boolean because for if (P) then Q;, the consequent Q is not executed if the antecedent P is false (although a compound as a whole is successful ≈ "true" in such case). This is closer to intuitionist and constructivist views on the material conditional— rather than to classical logic's views.
Set theory
[edit]Logical connectives are used to define the fundamental operations of set theory,[22] as follows:
| Set operation | Connective | Definition |
|---|---|---|
| Intersection | Conjunction | [23][24][25] |
| Union | Disjunction | [26][23][24] |
| Complement | Negation | [27][24][28] |
| Subset | Implication | [29][24][30] |
| Equality | Biconditional | [29][24][31] |
This definition of set equality is equivalent to the axiom of extensionality.
See also
[edit]References
[edit]- ^ Cogwheel. "What is the difference between logical and conditional /operator/". Stack Overflow. Retrieved 9 April 2015.
- ^ Chao, C. (2023). 数理逻辑:形式化方法的应用 [Mathematical Logic: Applications of the Formalization Method] (in Chinese). Beijing: Preprint. pp. 15–28.
- ^ a b Heyting, A. (1930). "Die formalen Regeln der intuitionistischen Logik". Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse (in German): 42–56.
- ^ Denis Roegel (2002), A brief survey of 20th century logical notations (see chart on page 2).
- ^ Frege, G. (1879). Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle a/S.: Verlag von Louis Nebert. p. 10.
- ^ a b c Russell (1908) Mathematical logic as based on the theory of types (American Journal of Mathematics 30, p222–262, also in From Frege to Gödel edited by van Heijenoort).
- ^ Peano (1889) Arithmetices principia, nova methodo exposita.
- ^ a b Schönfinkel (1924) Über die Bausteine der mathematischen Logik, translated as On the building blocks of mathematical logic in From Frege to Gödel edited by van Heijenoort.
- ^ Peirce (1867) On an improvement in Boole's calculus of logic.
- ^ Hilbert, D. (1918). Bernays, P. (ed.). Prinzipien der Mathematik. Lecture notes at Universität Göttingen, Winter Semester, 1917-1918; Reprinted as Hilbert, D. (2013). "Prinzipien der Mathematik". In Ewald, W.; Sieg, W. (eds.). David Hilbert's Lectures on the Foundations of Arithmetic and Logic 1917–1933. Heidelberg, New York, Dordrecht and London: Springer. pp. 59–221.
- ^ Bourbaki, N. (1954). Théorie des ensembles. Paris: Hermann & Cie, Éditeurs. p. 14.
- ^ Frege, G. (1879). Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens (in German). Halle a/S.: Verlag von Louis Nebert. p. 15.
- ^ Becker, A. (1933). Die Aristotelische Theorie der Möglichkeitsschlösse: Eine logisch-philologische Untersuchung der Kapitel 13-22 von Aristoteles' Analytica priora I (in German). Berlin: Junker und Dünnhaupt Verlag. p. 4.
- ^ Bourbaki, N. (1954). Théorie des ensembles (in French). Paris: Hermann & Cie, Éditeurs. p. 32.
- ^ Gentzen (1934) Untersuchungen über das logische Schließen.
- ^ Chazal (1996) : Éléments de logique formelle.
- ^ Hilbert, D. (1905) [1904]. "Über die Grundlagen der Logik und der Arithmetik". In Krazer, K. (ed.). Verhandlungen des Dritten Internationalen Mathematiker Kongresses in Heidelberg vom 8. bis 13. August 1904. pp. 174–185.
- ^ Bocheński (1959), A Précis of Mathematical Logic, passim.
- ^ O'Donnell, John; Hall, Cordelia; Page, Rex (2007), Discrete Mathematics Using a Computer, Springer, p. 120, ISBN 9781846285981.
- ^ Allen, Colin; Hand, Michael (2022). Logic primer (3rd ed.). Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-54364-4.
- ^ Jackson, Daniel (2012), Software Abstractions: Logic, Language, and Analysis, MIT Press, p. 263, ISBN 9780262017152.
- ^ Pinter, Charles C. (2014). A book of set theory. Mineola, New York: Dover Publications, Inc. pp. 26–29. ISBN 978-0-486-49708-2.
- ^ a b "Set operations". www.siue.edu. Retrieved 2024-06-11.
- ^ a b c d e "1.5 Logic and Sets". www.whitman.edu. Retrieved 2024-06-11.
- ^ "Theory Set". mirror.clarkson.edu. Retrieved 2024-06-11.
- ^ "Set Inclusion and Relations". autry.sites.grinnell.edu. Retrieved 2024-06-11.
- ^ "Complement and Set Difference". web.mnstate.edu. Retrieved 2024-06-11.
- ^ Cooper, A. "Set Operations and Subsets – Foundations of Mathematics". Retrieved 2024-06-11.
- ^ a b "Basic concepts". www.siue.edu. Retrieved 2024-06-11.
- ^ Cooper, A. "Set Operations and Subsets – Foundations of Mathematics". Retrieved 2024-06-11.
- ^ Cooper, A. "Set Operations and Subsets – Foundations of Mathematics". Retrieved 2024-06-11.
Sources
[edit]- Bocheński, Józef Maria (1959), A Précis of Mathematical Logic, translated from the French and German editions by Otto Bird, D. Reidel, Dordrecht, South Holland.
- Chao, C. (2023). 数理逻辑:形式化方法的应用 [Mathematical Logic: Applications of the Formalization Method] (in Chinese). Beijing: Preprint. pp. 15–28.
- Enderton, Herbert (2001), A Mathematical Introduction to Logic (2nd ed.), Boston, MA: Academic Press, ISBN 978-0-12-238452-3
- Gamut, L.T.F (1991), "Chapter 2", Logic, Language and Meaning, vol. 1, University of Chicago Press, pp. 54–64, OCLC 21372380
- Rautenberg, W. (2010), A Concise Introduction to Mathematical Logic (3rd ed.), New York: Springer Science+Business Media, doi:10.1007/978-1-4419-1221-3, ISBN 978-1-4419-1220-6.
- Humberstone, Lloyd (2011). The Connectives. MIT Press. ISBN 978-0-262-01654-4.
External links
[edit]- "Propositional connective", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Lloyd Humberstone (2010), "Sentence Connectives in Formal Logic", Stanford Encyclopedia of Philosophy (An abstract algebraic logic approach to connectives.)
- John MacFarlane (2005), "Logical constants", Stanford Encyclopedia of Philosophy.







































































































































![{\displaystyle A=B\leftrightarrow (\forall X)[A\in X\leftrightarrow B\in X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b9c356d049a459b2bde935a70b26587ff211b98)




