Lorenz system

Not to be confused with Lorenz curve or Lorentz distribution.

A sample solution in the Lorenz attractor when ρ = 28, σ = 10, and β = ⁠8/3⁠

The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. In popular media the "butterfly effect" stems from the real-world implications of the Lorenz attractor, namely that in a chaotic physical system, in the absence of perfect knowledge of the initial conditions (even the minuscule disturbance of the air due to a butterfly flapping its wings), our ability to predict its future course will always fail. This underscores that physical systems can be completely deterministic and yet still be inherently unpredictable. The shape of the Lorenz attractor itself, when plotted in phase space, may also be seen to resemble a butterfly.

Overview

In 1963, Edward Lorenz, with the help of Ellen Fetter who was responsible for the numerical simulations and figures, and Margaret Hamilton who helped in the initial, numerical computations leading up to the findings of the Lorenz model, developed a simplified mathematical model for atmospheric convection. The model is a system of three ordinary differential equations now known as the Lorenz equations:

${\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma (y-x),\\[6pt]{\frac {\mathrm {d} y}{\mathrm {d} t}}&=x(\rho -z)-y,\\[6pt]{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-\beta z.\end{aligned}}$

The equations relate the properties of a two-dimensional fluid layer uniformly warmed from below and cooled from above. In particular, the equations describe the rate of change of three quantities with respect to time: x is proportional to the rate of convection, y to the horizontal temperature variation, and z to the vertical temperature variation. The constants σ, ρ, and β are system parameters proportional to the Prandtl number, Rayleigh number, and certain physical dimensions of the layer itself.

The Lorenz equations can arise in simplified models for lasers, dynamos, thermosyphons, brushless DC motors, electric circuits, chemical reactions and forward osmosis. The Lorenz equations are also the governing equations in Fourier space for the Malkus waterwheel. The Malkus waterwheel exhibits chaotic motion where instead of spinning in one direction at a constant speed, its rotation will speed up, slow down, stop, change directions, and oscillate back and forth between combinations of such behaviors in an unpredictable manner.

From a technical standpoint, the Lorenz system is nonlinear, aperiodic, three-dimensional and deterministic. The Lorenz equations have been the subject of hundreds of research articles, and at least one book-length study.

Analysis

One normally assumes that the parameters σ, ρ, and β are positive. Lorenz used the values σ = 10, β = ⁠8/3⁠ and ρ = 28. The system exhibits chaotic behavior for these (and nearby) values.

If ρ < 1 then there is only one equilibrium point, which is at the origin. This point corresponds to no convection. All orbits converge to the origin, which is a global attractor, when ρ < 1.

A pitchfork bifurcation occurs at ρ = 1, and for ρ > 1 two additional critical points appear at

$\left({\sqrt {\beta (\rho -1)}},{\sqrt {\beta (\rho -1)}},\rho -1\right)\quad {\text{and}}\quad \left(-{\sqrt {\beta (\rho -1)}},-{\sqrt {\beta (\rho -1)}},\rho -1\right).$

These correspond to steady convection. This pair of equilibrium points is stable only if

$\rho <\sigma {\frac {\sigma +\beta +3}{\sigma -\beta -1}},$

which can hold only for positive ρ if σ > β + 1. At the critical value, both equilibrium points lose stability through a subcritical Hopf bifurcation.

When ρ = 28, σ = 10, and β = ⁠8/3⁠, the Lorenz system has chaotic solutions (but not all solutions are chaotic). Almost all initial points will tend to an invariant set – the Lorenz attractor – a strange attractor, a fractal, and a self-excited attractor with respect to all three equilibria. Its Hausdorff dimension is estimated from above by the Lyapunov dimension (Kaplan-Yorke dimension) as 2.06±0.01, and the correlation dimension is estimated to be 2.05±0.01. The exact Lyapunov dimension formula of the global attractor can be found analytically under classical restrictions on the parameters:

$3-{\frac {2(\sigma +\beta +1)}{\sigma +1+{\sqrt {\left(\sigma -1\right)^{2}+4\sigma \rho }}}}$

The Lorenz attractor is difficult to analyze, but the action of the differential equation on the attractor is described by a fairly simple geometric model. Proving that this is indeed the case is the fourteenth problem on the list of Smale's problems. This problem was the first one to be resolved, by Warwick Tucker in 2002.

For other values of ρ, the system displays knotted periodic orbits. For example, with ρ = 99.96 it becomes a T(3,2) torus knot.

Example solutions of the Lorenz system for different values of ρ
ρ = 14, σ = 10, β = ⁠8/3⁠ (Enlarge)	ρ = 13, σ = 10, β = ⁠8/3⁠ (Enlarge)
ρ = 15, σ = 10, β = ⁠8/3⁠ (Enlarge)	ρ = 28, σ = 10, β = ⁠8/3⁠ (Enlarge)
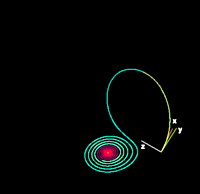
For small values of ρ, the system is stable and evolves to one of two fixed point attractors. When ρ > 24.74, the fixed points become repulsors and the trajectory is repelled by them in a very complex way.

Sensitive dependence on the initial condition
Time t = 1 (Enlarge)	Time t = 2 (Enlarge)	Time t = 3 (Enlarge)
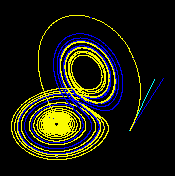
These figures — made using ρ = 28, σ = 10 and β = ⁠8/3⁠ — show three time segments of the 3-D evolution of two trajectories (one in blue, the other in yellow) in the Lorenz attractor starting at two initial points that differ only by 10−5 in the x-coordinate. Initially, the two trajectories seem coincident (only the yellow one can be seen, as it is drawn over the blue one) but, after some time, the divergence is obvious.

Connection to tent map

A recreation of Lorenz's results created on Mathematica. Points above the red line correspond to the system switching lobes.

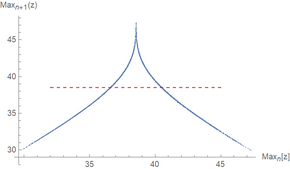
In Figure 4 of his paper, Lorenz plotted the relative maximum value in the z direction achieved by the system against the previous relative maximum in the z direction. This procedure later became known as a Lorenz map (not to be confused with a Poincaré plot, which plots the intersections of a trajectory with a prescribed surface). The resulting plot has a shape very similar to the tent map. Lorenz also found that when the maximum z value is above a certain cut-off, the system will switch to the next lobe. Combining this with the chaos known to be exhibited by the tent map, he showed that the system switches between the two lobes chaotically.

A Generalized Lorenz System

Over the past several years, a series of papers regarding high-dimensional Lorenz models have yielded a generalized Lorenz model, which can be simplified into the classical Lorenz model for three state variables or the following five-dimensional Lorenz model for five state variables: $${\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma (y-x),\\[6pt]{\frac {\mathrm {d} y}{\mathrm {d} t}}&=x(\rho -z)-y,\\[6pt]{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-xy_{1}-\beta z,\\[6pt]{\frac {\mathrm {d} y_{1}}{\mathrm {d} t}}&=xz-2xz_{1}-d_{0}y_{1},\\[6pt]{\frac {\mathrm {d} z_{1}}{\mathrm {d} t}}&=2xy_{1}-4\beta z_{1}.\end{aligned}}$$

A choice of the parameter d₀ = 19/3 has been applied to be consistent with the choice of the other parameters. See details in.

Simulations

Julia simulation

using DifferentialEquations, Plots
function lorenz!(du,u,p,t)
    du[1] = 10.0*(u[2]-u[1])
    du[2] = u[1]*(28.0-u[3]) - u[2]
    du[3] = u[1]*u[2] - (8/3)*u[3]
end
u0 = [1.0;0.0;0.0]
tspan = (0.0,100.0)
prob = ODEProblem(lorenz!,u0,tspan)
sol = solve(prob)
plot(sol,vars=(1,2,3))

MATLAB simulation

% Solve over time interval [0,100] with initial conditions [1,1,1]
% ''f'' is set of differential equations
% ''a'' is array containing x, y, and z variables
% ''t'' is time variable

sigma = 10;
beta = 8/3;
rho = 28;
f = @(t,a) [-sigma*a(1) + sigma*a(2); rho*a(1) - a(2) - a(1)*a(3); -beta*a(3) + a(1)*a(2)];
[t,a] = ode45(f,[0 100],[1 1 1]);     % Runge-Kutta 4th/5th order ODE solver
plot3(a(:,1),a(:,2),a(:,3))

Mathematica simulation

Standard way:

tend = 50;
eq = {x'[t] == σ (y[t] - x[t]), 
      y'[t] == x[t] (ρ - z[t]) - y[t], 
      z'[t] == x[t] y[t] - β z[t]};
init = {x[0] == 10, y[0] == 10, z[0] == 10};
pars = {σ->10, ρ->28, β->8/3};
{xs, ys, zs} = 
  NDSolveValue[{eq /. pars, init}, {x, y, z}, {t, 0, tend}];
ParametricPlot3D[{xs[t], ys[t], zs[t]}, {t, 0, tend}]

Less verbose:

lorenz = NonlinearStateSpaceModel[{{σ (y - x), x (ρ - z) - y, x y - β z}, {}}, {x, y, z}, {σ, ρ, β}];
soln[t_] = StateResponse[{lorenz, {10, 10, 10}}, {10, 28, 8/3}, {t, 0, 50}];
ParametricPlot3D[soln[t], {t, 0, 50}]

Python simulation

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D

rho = 28.0
sigma = 10.0
beta = 8.0 / 3.0

def f(state, t):
    x, y, z = state  # Unpack the state vector
    return sigma * (y - x), x * (rho - z) - y, x * y - beta * z  # Derivatives

state0 = [1.0, 1.0, 1.0]
t = np.arange(0.0, 40.0, 0.01)

states = odeint(f, state0, t)

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot(states[:, 0], states[:, 1], states[:, 2])
plt.draw()
plt.show()

Python code for the five-dimensional Lorenz system

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D

rho = 43.5
sigma = 10.0
beta = 8.0 / 3.0
d0 = 19.0 / 3.0 

def f(state, t):
    x, y, z, y1, z1 = state  # Unpack the state vector
    return sigma * (y - x), x * (rho - z) - y, x * y - x * y1 - beta * z, x * z - 2 * x * z1 - d0 * y1, 2 * x * y1 - 4 * beta * z1  # Derivatives

state0 = [1.0, 1.0, 1.0, 1.0, 1.0]
t = np.arange(0.0, 40.0, 0.01)

states = odeint(f, state0, t)

fig, ax = plt.subplots(subplot_kw=dict(projection='3d'))
ax.plot(states[:, 0], states[:, 1], states[:, 2])
plt.draw()
plt.show()

Applications

Model for atmospheric convection

As shown in Lorenz's original paper, the Lorenz system is a reduced version of a larger system studied earlier by Barry Saltzman. The Lorenz equations are derived from the Oberbeck–Boussinesq approximation to the equations describing fluid circulation in a shallow layer of fluid, heated uniformly from below and cooled uniformly from above. This fluid circulation is known as Rayleigh–Bénard convection. The fluid is assumed to circulate in two dimensions (vertical and horizontal) with periodic rectangular boundary conditions.

The partial differential equations modeling the system's stream function and temperature are subjected to a spectral Galerkin approximation: the hydrodynamic fields are expanded in Fourier series, which are then severely truncated to a single term for the stream function and two terms for the temperature. This reduces the model equations to a set of three coupled, nonlinear ordinary differential equations. A detailed derivation may be found, for example, in nonlinear dynamics texts from Hilborn (2000), Appendix C; 1984 Bergé, Pomeau & Vidal (1984), Appendix D; or Shen (2016), Supplementary Materials.

Resolution of Smale's 14th problem

Smale's 14th problem says, 'Do the properties of the Lorenz attractor exhibit that of a strange attractor?'. The problem was answered affirmatively by Warwick Tucker in 2002. To prove this result, Tucker used rigorous numerics methods like interval arithmetic and normal forms. First, Tucker defined a cross section $\Sigma \subset \{x_{3}=r-1\}$ that is cut transversely by the flow trajectories. From this, one can define the first-return map $P$, which assigns to each $x\in \Sigma$ the point $P(x)$ where the trajectory of $x$ first intersects $\Sigma$.

Then the proof is split in three main points that are proved and imply the existence of a strange attractor. The three points are:

• There exists a region $N\subset \Sigma$ invariant under the first-return map, meaning $P(N)\subset N$.
• The return map admits a forward invariant cone field.
• Vectors inside this invariant cone field are uniformly expanded by the derivative $DP$ of the return map.

To prove the first point, we notice that the cross section $\Sigma$ is cut by two arcs formed by $P(\Sigma )$. Tucker covers the location of these two arcs by small rectangles $R_{i}$, the union of these rectangles gives $N$. Now, the goal is to prove that for all points in $N$, the flow will bring back the points in $\Sigma$, in $N$. To do that, we take a plan $\Sigma '$ below $\Sigma$ at a distance $h$ small, then by taking the center $c_{i}$ of $R_{i}$ and using Euler integration method, one can estimate where the flow will bring $c_{i}$ in $\Sigma '$ which gives us a new point $c_{i}'$. Then, one can estimate where the points in $\Sigma$ will be mapped in $\Sigma '$ using Taylor expansion, this gives us a new rectangle $R_{i}'$ centered on $c_{i}$. Thus we know that all points in $R_{i}$ will be mapped in $R_{i}'$. The goal is to do this method recursively until the flow comes back to $\Sigma$ and we obtain a rectangle $Rf_{i}$ in $\Sigma$ such that we know that $P(R_{i})\subset Rf_{i}$. The problem is that our estimation may become imprecise after several iterations, thus what Tucker does is to split $R_{i}'$ into smaller rectangles $R_{i,j}$ and then apply the process recursively. Another problem is that as we are applying this algorithm, the flow becomes more 'horizontal', leading to a dramatic increase in imprecision. To prevent this, the algorithm changes the orientation of the cross sections, becoming either horizontal or vertical.

Gallery

• 
  A solution in the Lorenz attractor plotted at high resolution in the xz plane.
• 
  A solution in the Lorenz attractor rendered as an SVG.
• An animation showing trajectories of multiple solutions in a Lorenz system.
• 
  A solution in the Lorenz attractor rendered as a metal wire to show direction and 3D structure.
• An animation showing the divergence of nearby solutions to the Lorenz system.
• 
  A visualization of the Lorenz attractor near an intermittent cycle.
• 
  Two streamlines in a Lorenz system, from ρ = 0 to ρ = 28 (σ = 10, β = ⁠8/3⁠).
• 
  Animation of a Lorenz System with rho-dependence.
• 
  Animation of the Lorenz attractor in the Brain Dynamics Toolbox.

See also

• Eden's conjecture on the Lyapunov dimension
• Lorenz 96 model
• List of chaotic maps
• Takens' theorem

References

• Bergé, Pierre; Pomeau, Yves; Vidal, Christian (1984). Order within Chaos: Towards a Deterministic Approach to Turbulence. New York: John Wiley & Sons. ISBN 978-0-471-84967-4.
• Cuomo, Kevin M.; Oppenheim, Alan V. (1993). "Circuit implementation of synchronized chaos with applications to communications". Physical Review Letters. 71 (1): 65–68. Bibcode:1993PhRvL..71...65C. doi:10.1103/PhysRevLett.71.65. ISSN 0031-9007. PMID 10054374.
• Gorman, M.; Widmann, P.J.; Robbins, K.A. (1986). "Nonlinear dynamics of a convection loop: A quantitative comparison of experiment with theory". Physica D. 19 (2): 255–267. Bibcode:1986PhyD...19..255G. doi:10.1016/0167-2789(86)90022-9.
• Grassberger, P.; Procaccia, I. (1983). "Measuring the strangeness of strange attractors". Physica D. 9 (1–2): 189–208. Bibcode:1983PhyD....9..189G. doi:10.1016/0167-2789(83)90298-1.
• Haken, H. (1975). "Analogy between higher instabilities in fluids and lasers". Physics Letters A. 53 (1): 77–78. Bibcode:1975PhLA...53...77H. doi:10.1016/0375-9601(75)90353-9.
• Hemati, N. (1994). "Strange attractors in brushless DC motors". IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. 41 (1): 40–45. doi:10.1109/81.260218. ISSN 1057-7122.
• Hilborn, Robert C. (2000). Chaos and Nonlinear Dynamics: An Introduction for Scientists and Engineers (second ed.). Oxford University Press. ISBN 978-0-19-850723-9.
• Hirsch, Morris W.; Smale, Stephen; Devaney, Robert (2003). Differential Equations, Dynamical Systems, & An Introduction to Chaos (Second ed.). Boston, MA: Academic Press. ISBN 978-0-12-349703-1.
• Knobloch, Edgar (1981). "Chaos in the segmented disc dynamo". Physics Letters A. 82 (9): 439–440. Bibcode:1981PhLA...82..439K. doi:10.1016/0375-9601(81)90274-7.
• Kolář, Miroslav; Gumbs, Godfrey (1992). "Theory for the experimental observation of chaos in a rotating waterwheel". Physical Review A. 45 (2): 626–637. Bibcode:1992PhRvA..45..626K. doi:10.1103/PhysRevA.45.626. PMID 9907027.
• Leonov, G.A.; Kuznetsov, N.V.; Korzhemanova, N.A.; Kusakin, D.V. (2016). "Lyapunov dimension formula for the global attractor of the Lorenz system". Communications in Nonlinear Science and Numerical Simulation. 41: 84–103. arXiv:1508.07498. Bibcode:2016CNSNS..41...84L. doi:10.1016/j.cnsns.2016.04.032. S2CID 119614076.
• Lorenz, Edward Norton (1963). "Deterministic nonperiodic flow". Journal of the Atmospheric Sciences. 20 (2): 130–141. Bibcode:1963JAtS...20..130L. doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2.
• Mishra, Aashwin; Sanghi, Sanjeev (2006). "A study of the asymmetric Malkus waterwheel: The biased Lorenz equations". Chaos: An Interdisciplinary Journal of Nonlinear Science. 16 (1): 013114. Bibcode:2006Chaos..16a3114M. doi:10.1063/1.2154792. PMID 16599745.
• Pchelintsev, A.N. (2014). "Numerical and Physical Modeling of the Dynamics of the Lorenz System". Numerical Analysis and Applications. 7 (2): 159–167. doi:10.1134/S1995423914020098. S2CID 123023929.
• Poland, Douglas (1993). "Cooperative catalysis and chemical chaos: a chemical model for the Lorenz equations". Physica D. 65 (1): 86–99. Bibcode:1993PhyD...65...86P. doi:10.1016/0167-2789(93)90006-M.
• Saltzman, Barry (1962). "Finite Amplitude Free Convection as an Initial Value Problem—I". Journal of the Atmospheric Sciences. 19 (4): 329–341. Bibcode:1962JAtS...19..329S. doi:10.1175/1520-0469(1962)019<0329:FAFCAA>2.0.CO;2.
• Shen, B.-W. (2015-12-21). "Nonlinear feedback in a six-dimensional Lorenz model: impact of an additional heating term". Nonlinear Processes in Geophysics. 22 (6): 749–764. doi:10.5194/npg-22-749-2015. ISSN 1607-7946.
• Sparrow, Colin (1982). The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors. Springer.
• Tucker, Warwick (2002). "A Rigorous ODE Solver and Smale's 14th Problem" (PDF). Foundations of Computational Mathematics. 2 (1): 53–117. CiteSeerX 10.1.1.545.3996. doi:10.1007/s002080010018. S2CID 353254.
• Tzenov, Stephan (2014). "Strange Attractors Characterizing the Osmotic Instability". arXiv:1406.0979v1 [physics.flu-dyn].
• Viana, Marcelo (2000). "What's new on Lorenz strange attractors?". The Mathematical Intelligencer. 22 (3): 6–19. doi:10.1007/BF03025276. S2CID 121427433.
• Lorenz, Edward N. (1960). "The statistical prediction of solutions of dynamic equations" (PDF). Symposium on Numerical Weather Prediction in Tokyo.

Further reading

• G.A. Leonov & N.V. Kuznetsov (2015). "On differences and similarities in the analysis of Lorenz, Chen, and Lu systems" (PDF). Applied Mathematics and Computation. 256: 334–343. doi:10.1016/j.amc.2014.12.132.
• Pchelintsev, A.N. (2022). "On a high-precision method for studying attractors of dynamical systems and systems of explosive type". Mathematics. 10 (8): 1207. arXiv:2206.08195. doi:10.3390/math10081207.

External links

• "Lorenz attractor", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Lorenz attractor". MathWorld.
• Lorenz attractor by Rob Morris, Wolfram Demonstrations Project.
• Lorenz equation on planetmath.org
• Synchronized Chaos and Private Communications, with Kevin Cuomo. The implementation of Lorenz attractor in an electronic circuit.
• Lorenz attractor interactive animation (you need the Adobe Shockwave plugin)
• 3D Attractors: Mac program to visualize and explore the Lorenz attractor in 3 dimensions
• Lorenz Attractor implemented in analog electronic
• Lorenz Attractor interactive animation (implemented in Ada with GTK+. Sources & executable)
• Web based Lorenz Attractor (implemented in JavaScript/HTML/CSS)
• Interactive web based Lorenz Attractor made with Iodide