Near sets

In mathematics, near sets are either spatially close or descriptively close. Spatially close sets have nonempty intersection. In other words, spatially close sets are not disjoint sets, since they always have at least one element in common. Descriptively close sets contain elements that have matching descriptions. Such sets can be either disjoint or non-disjoint sets. Spatially near sets are also descriptively near sets.

The underlying assumption with descriptively close sets is that such sets contain elements that have location and measurable features such as colour and frequency of occurrence. The description of the element of a set is defined by a feature vector. Comparison of feature vectors provides a basis for measuring the closeness of descriptively near sets. Near set theory provides a formal basis for the observation, comparison, and classification of elements in sets based on their closeness, either spatially or descriptively. Near sets offer a framework for solving problems based on human perception that arise in areas such as image processing, computer vision as well as engineering and science problems.
Near sets have a variety of applications in areas such as topology[37], pattern detection and classification[50], abstract algebra[51], mathematics in computer science[38], and solving a variety of problems based on human perception[42][82][47][52][56] that arise in areas such as image analysis[54][14][46][17][18], image processing[40], face recognition[13], ethology[64], as well as engineering and science problems[55][64][42][19][17][18]. From the beginning, descriptively near sets have proved to be useful in applications of topology[37], and visual pattern recognition [50], spanning a broad spectrum of applications that include camouflage detection, micropaleontology, handwriting forgery detection, biomedical image analysis, content-based image retrieval, population dynamics, quotient topology, textile design, visual merchandising, and topological psychology.
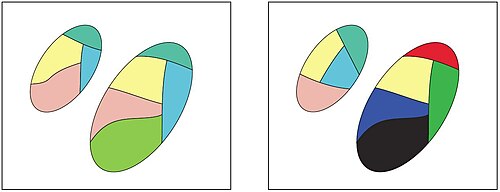
As an illustration of the degree of descriptive nearness between two sets, consider an example of the Henry colour model for varying degrees of nearness between sets of picture elements in pictures (see, e.g.,[17] §4.3). The two pairs of ovals in Fig. 1 and Fig. 2 contain coloured segments. Each segment in the figures corresponds to an equivalence class where all pixels in the class have similar descriptions, i.e., picture elements with similar colours. The ovals in Fig.1 are closer to each other descriptively than the ovals in Fig. 2.
History[edit]
It has been observed that the simple concept of nearness unifies various concepts of topological structures[20] inasmuch as the category Near of all nearness spaces and nearness preserving maps contains categories sTop (symmetric topological spaces and continuous maps[3]), Prox (proximity spaces and -maps[8][67]), Unif (uniform spaces and uniformly continuous maps[81][77]) and Cont (contiguity spaces and contiguity maps[24]) as embedded full subcategories[20][59]. The categories and are shown to be full supercategories of various well-known categories, including the category of symmetric topological spaces and continuous maps, and the category of extended metric spaces and nonexpansive maps. The notation reads category is embedded in category . The categories and are supercategories for a variety of familiar categories[76] shown in Fig. 3. Let denote the category of all -approach nearness spaces and contractions, and let denote the category of all -approach merotopic spaces and contractions.

Among these familiar categories is , the symmetric form of (see category of topological spaces), the category with objects that are topological spaces and morphisms that are continuous maps between them[1][32]. with objects that are extended metric spaces is a subcategory of (having objects -approach spaces and contractions) (see also[57][75]). Let be extended pseudometrics on nonempty sets , respectively. The map is a contraction if and only if is a contraction. For nonempty subsets , the distance function is defined by
Thus AP is embedded as a full subcategory in by the functor defined by and . Then is a contraction if and only if is a contraction. Thus is embedded as a full subcategory in by the functor defined by and Since the category of extended metric spaces and nonexpansive maps is a full subcategory of , therefore, is also a full supercategory of . The category is a topological construct[76].

The notions of near and far[A] in mathematics can be traced back to works by Johann Benedict Listing and Felix Hausdorff. The related notions of resemblance and similarity can be traced back to J.H. Poincaré, who introduced sets of similar sensations (nascent tolerance classes) to represent the results of G.T. Fechner's sensation sensitivity experiments[10] and a framework for the study of resemblance in representative spaces as models of what he termed physical continua[63][60][61]. The elements of a physical continuum (pc) are sets of sensations. The notion of a pc and various representative spaces (tactile, visual, motor spaces) were introduced by Poincaré in an 1894 article on the mathematical continuum[63], an 1895 article on space and geometry[60] and a compendious 1902 book on science and hypothesis[61] followed by a number of elaborations, e.g.,[62]. The 1893 and 1895 articles on continua (Pt. 1, ch. II) as well as representative spaces and geometry (Pt. 2, ch IV) are included as chapters in[61]. Later, F. Riesz introduced the concept of proximity or nearness of pairs of sets at the International Congress of Mathematicians (ICM) in 1908[65].
During the 1960s, E.C. Zeeman introduced tolerance spaces in modelling visual perception[83]. A.B. Sossinsky observed in 1986[71] that the main idea underlying tolerance space theory comes from Poincaré, especially[60]. In 2002, Z. Pawlak and J. Peters[B] considered an informal approach to the perception of the nearness of physical objects such as snowflakes that was not limited to spatial nearness. In 2006, a formal approach to the descriptive nearness of objects was considered by J. Peters, A. Skowron and J. Stepaniuk[C] in the context of proximity spaces[39][33][35][21]. In 2007, descriptively near sets were introduced by J. Peters[D][E] followed by the introduction of tolerance near sets[41][45]. Recently, the study of descriptively near sets has led to algebraic[22][51], topological and proximity space[37] foundations of such sets.
Nearness of sets[edit]
The adjective near in the context of near sets is used to denote the fact that observed feature value differences of distinct objects are small enough to be considered indistinguishable, i.e., within some tolerance.
The exact idea of closeness or 'resemblance' or of 'being within tolerance' is universal enough to appear, quite naturally, in almost any mathematical setting (see, e.g.,[66]). It is especially natural in mathematical applications: practical problems, more often than not, deal with approximate input data and only require viable results with a tolerable level of error[71].
The words near and far are used in daily life and it was an incisive suggestion of F. Riesz[65] that these intuitive concepts be made rigorous. He introduced the concept of nearness of pairs of sets at the ICM in Rome in 1908. This concept is useful in simplifying teaching calculus and advanced calculus. For example, the passage from an intuitive definition of continuity of a function at a point to its rigorous epsilon-delta definition is sometime difficult for teachers to explain and for students to understand. Intuitively, continuity can be explained using nearness language, i.e., a function is continuous at a point , provided points near go into points near . Using Riesz's idea, this definition can be made more precise and its contrapositive is the familiar definition[4][36].
Generalization of set intersection[edit]
From a spatial point of view, nearness (a.k.a. proximity) is considered a generalization of set intersection. For disjoint sets, a form of nearness set intersection is defined in terms of a set of objects (extracted from disjoint sets) that have similar features within some tolerance (see, e.g., §3 in[80]). For example, the ovals in Fig. 1 are considered near each other, since these ovals contain pairs of classes that display similar (visually indistinguishable) colours.
Efremovič proximity space[edit]
Let denote a metric topological space that is endowed with one or more proximity relations and let denote the collection of all subsets of . The collection is called the power set of .
There are many ways to define Efremovič proximities on topological spaces (discrete proximity, standard proximity, metric proximity, Čech proximity, Alexandroff proximity, and Freudenthal proximity), For details, see § 2, pp. 93–94 in[6]. The focus here is on standard proximity on a topological space. For , is near (denoted by ), provided their closures share a common point.
The closure of a subset (denoted by ) is the usual Kuratowski closure of a set[F], introduced in § 4, p. 20[27], is defined by
I.e., is the set of all points in that are close to ( is the Hausdorff distance (see § 22, p. 128, in[15]) between and the set and (standard distance)). A standard proximity relation is defined by
Whenever sets and have no points in common, the sets are farfrom each other (denoted ).
The following EF-proximity[G] space axioms are given by Jurij Michailov Smirnov[67] based on what Vadim Arsenyevič Efremovič introduced during the first half of the 1930s[8]. Let .
- EF.1
- If the set is close to , then is close to .
- EF.2
- is close to , if and only if, at least one of the sets or is close to .
- EF.3
- Two points are close, if and only if, they are the same point.
- EF.4
- All sets are far from the empty set .
- EF.5
- For any two sets and which are far from each other, there exists , , such that is far from and is far from (Efremovič-axiom).
The pair is called an EF-proximity space. In this context, a space is a set with some added structure. With a proximity space , the structure of is induced by the EF-proximity relation . In a proximity space , the closure of in coincides with the intersection of all closed sets that contain .
- Theorem 1[67]
- The closure of any set in the proximity space is the set of points that are close to .
Visualization of EF-axiom[edit]

Let the set be represented by the points inside the rectangular region in Fig. 5. Also, let be any two non-intersection subsets (i.e. subsets spatially far from each other) in , as shown in Fig. 5. Let (complement of the set ). Then from the EF-axiom, observe the following:
Descriptive proximity space[edit]
Descriptively near sets were introduced as a means of solving classification and pattern recognition problems arising from disjoint sets that resemble each other.[44][43] Recently, the connections between near sets in EF-spaces and near sets in descriptive EF-proximity spaces have been explored in.[53][48]
Again, let be a metric topological space and let a set of probe functions that represent features of each . The assumption made here is contains non-abstract points that have measurable features such as gradient orientation. A non-abstract point has a location and features that can be measured (see § 3 in [26]).
A probe function represents a feature of a sample point in . The mapping is defined by , where is an n-dimensional real Euclidean vector space. is a feature vector for , which provides a description of . For example, this leads to a proximal view of sets of picture points in digital images.[48]
To obtain a descriptive proximity relation (denoted by ), one first chooses a set of probe functions. Let be a mapping on a subset of into a subset of . For example, let and denote sets of descriptions of points in , respectively. That is,
The expression reads is descriptively near . Similarly, reads is descriptively far from . The descriptive proximity of and is defined by
The descriptive intersection of and is defined by
That is, is in , provided for some . Observe that and can be disjoint and yet can be nonempty.
The descriptive proximity relation is defined by
Whenever sets and have no points with matching descriptions, the sets are descriptively far from each other (denoted by ).
The binary relation is a descriptive EF-proximity, provided the following axioms are satisfied for .
- dEF.1
- If the set is descriptively close to , then is descriptively close to .
- dEF.2
- is descriptively close to , if and only if, at least one of the sets or is descriptively close to .
- dEF.3
- Two points are descriptively close, if and only if, the description of matches the description of .
- dEF.4
- All nonempty sets are descriptively far from the empty set .
- dEF.5
- For any two sets and which are descriptively far from each other, there exists , , such that is descriptively far from and is descriptively far from (Descriptive Efremovič axiom).
The pair is called a descriptive proximity space.
Proximal relator spaces[edit]
A relator is a nonvoid family of relations on a nonempty set [72]. The pair (also denoted ) is called a relator space. Relator spaces are natural generalizations of ordered sets and uniform spaces.[73][74] With the introduction of a family of proximity relations on , we obtain a proximal relator space . For simplicity, we consider only two proximity relations, namely, the Efremovič proximity [8] and the descriptive proximity in defining the descriptive relator .[53][48] The pair is called a proximal relator space[49]. In this work, denotes a metric topological space that is endowed with the relations in a proximal relator. With the introduction of , the traditional closure of a subset (e.g., [9][7]) can be compared with the more recent descriptive closure of a subset.
In a proximal relator space , the descriptive closure of a set (denoted by ) is defined by
That is, is in the descriptive closure of , provided the closure of and the closure of have at least one element in common.
- Theorem 2 [50]
- The descriptive closure of any set in the descriptive EF-proximity space is the set of points that are descriptively close to .
- Theorem 3 [50]
- Kuratowski closure of a set is a subset of the descriptive closure of in a descriptive EF-proximity space.
- Theorem 4 [49]
- Let be a proximal relator space, . Then .
- Proof
- Let such that for some . Consequently, . Hence,
In a proximal relator space, EF-proximity leads to the following results for descriptive proximity .
- Theorem 5[49]
- Let be a proximal relator space, . Then
- 1°
- .
- 2°
- .
- 3°
- .
- Proof
-
- 1°
- . For and . Consequently, .
- 1° ⇒ 2°
- 3°
- implies that and have at least one point in common. Hence, 1° ⇒ 3°.
Descriptive 𝛿-neighbourhoods[edit]

In a pseudometric proximal relator space , the neighbourhood of a point (denoted by ), for , is defined by
The interior of a set (denoted by ) and boundary of (denoted by ) in a proximal relator space are defined by
A set has a natural strong inclusion in a set associated with [5][6]} (denoted by ), provided ; i.e., ( is far from the complement of ). Correspondingly, a set has a descriptive strong inclusion in a set associated with (denoted by ), provided ; i.e., ( is far from the complement of ).
Let be a descriptive -neighbourhood relation defined by
That is, , provided the description of each is contained in the set of descriptions of the points . Now observe that any in the proximal relator space such that have disjoint -neighbourhoods; i.e.,
- Theorem 6 [50]
- Any two sets descriptively far from each other belong to disjoint descriptive -neighbourhoods in a descriptive proximity space .
A consideration of strong containment of a nonempty set in another set leads to the study of hit-and-miss topologies and the Wijsman topology.[2]
Tolerance near sets[edit]
Let be a real number greater than zero. In the study of sets that are proximally near within some tolerance, the set of proximity relations is augmented with a pseudometric tolerance proximity relation (denoted by ) defined by
Let . In other words, a nonempty set equipped with the proximal relator has underlying structure provided by the proximal relator and provides a basis for the study of tolerance near sets in that are near within some tolerance. Sets in a descriptive pseudometric proximal relator space are tolerance near sets (i.e., ), provided
Tolerance classes and preclasses[edit]
Relations with the same formal properties as similarity relations of sensations considered by Poincaré[62] are nowadays, after Zeeman[83], called tolerance relations. A tolerance on a set is a relation that is reflexive and symmetric. In algebra, the term tolerance relation is also used in a narrow sense to denote reflexive and symmetric relations defined on universes of algebras that are also compatible with operations of a given algebra, i.e., they are generalizations of congruence relations (see e.g.,[12]). In referring to such relations, the term algebraic tolerance or the term algebraic tolerance relation is used. Transitive tolerance relations are equivalence relations. A set together with a tolerance is called a tolerance space (denoted ). A set is a -preclass (or briefly preclass when is understood) if and only if for any , .
The family of all preclasses of a tolerance space is naturally ordered by set inclusion and preclasses that are maximal with respect to set inclusion are called -classes or just classes, when is understood. The family of all classes of the space is particularly interesting and is denoted by . The family is a covering of [58].
The work on similarity by Poincaré and Zeeman presage the introduction of near sets[44][43] and research on similarity relations, e.g.,[79]. In science and engineering, tolerance near sets are a practical application of the study of sets that are near within some tolerance. A tolerance is directly related to the idea of closeness or resemblance (i.e., being within some tolerance) in comparing objects. By way of application of Poincaré's approach in defining visual spaces and Zeeman's approach to tolerance relations, the basic idea is to compare objects such as image patches in the interior of digital images.
Examples[edit]
Simple example
The following simple example demonstrates the construction of tolerance classes from real data. Consider the 20 objects in the table below with .
Sample perceptual system .4518 .6943 .4002 .6079 .9166 .9246 .1910 .1869 .1398 .3537 .7476 .8489 .7972 .4722 .4990 .9170 .6281 .4523 .6289 .7143
Let a tolerance relation be defined as
Then, setting gives the following tolerance classes:
Observe that each object in a tolerance class satisfies the condition , and that almost all of the objects appear in more than one class. Moreover, there would be twenty classes if the indiscernibility relation was used since there are no two objects with matching descriptions.
Image processing example

The following example provides an example based on digital images. Let a subimage be defined as a small subset of pixels belonging to a digital image such that the pixels contained in the subimage form a square. Then, let the sets and respectively represent the subimages obtained from two different images, and let . Finally, let the description of an object be given by the Green component in the RGB color model. The next step is to find all the tolerance classes using the tolerance relation defined in the previous example. Using this information, tolerance classes can be formed containing objects that have similar (within some small ) values for the Green component in the RGB colour model. Furthermore, images that are near (similar) to each other should have tolerance classes divided among both images (instead of a tolerance classes contained solely in one of the images). For example, the figure accompanying this example shows a subset of the tolerance classes obtained from two leaf images. In this figure, each tolerance class is assigned a separate colour. As can be seen, the two leaves share similar tolerance classes. This example highlights a need to measure the degree of nearness of two sets.
Nearness measure[edit]
Let denote a particular descriptive pseudometric EF-proximal relator space equipped with the proximity relation and with nonempty subsets and with the tolerance relation defined in terms of a set of probes and with , where
Further, assume and let denote the family of all classes in the space .
Let . The distance is defined by
where
The details concerning are given in[14][16][17]. The idea behind is that sets that are similar should have a similar number of objects in each tolerance class. Thus, for each tolerance class obtained from the covering of , counts the number of objects that belong to and and takes the ratio (as a proper fraction) of their cardinalities. Furthermore, each ratio is weighted by the total size of the tolerance class (thus giving importance to the larger classes) and the final result is normalized by dividing by the sum of all the cardinalities. The range of is in the interval [0,1], where a value of 1 is obtained if the sets are equivalent (based on object descriptions) and a value of 0 is obtained if they have no descriptions in common.
As an example of the degree of nearness between two sets, consider figure below in which each image consists of two sets of objects, and . Each colour in the figures corresponds to a set where all the objects in the class share the same description. The idea behind is that the nearness of sets in a perceptual system is based on the cardinality of tolerance classes that they share. Thus, the sets in left side of the figure are closer (more near) to each other in terms of their descriptions than the sets in right side of the figure.
Near set evaluation and recognition (NEAR) system[edit]

The Near set Evaluation and Recognition (NEAR) system, is a system developed to demonstrate practical applications of near set theory to the problems of image segmentation evaluation and image correspondence. It was motivated by a need for a freely available software tool that can provide results for research and to generate interest in near set theory. The system implements a Multiple Document Interface (MDI) where each separate processing task is performed in its own child frame. The objects (in the near set sense) in this system are subimages of the images being processed and the probe functions (features) are image processing functions defined on the subimages. The system was written in C++ and was designed to facilitate the addition of new processing tasks and probe functions. Currently, the system performs six major tasks, namely, displaying equivalence and tolerance classes for an image, performing segmentation evaluation, measuring the nearness of two images, performing Content Based Image Retrieval (CBIR), and displaying the output of processing an image using a specific probe function.
Proximity System[edit]

The Proximity System is an application developed to demonstrate descriptive-based topological approaches to nearness and proximity within the context of digital image analysis. The Proximity System grew out of the work of S. Naimpally and J. Peters on Topological Spaces. The Proximity System was written in Java and is intended to run in two different operating environments, namely on Android smartphones and tablets, as well as desktop platforms running the Java Virtual Machine. With respect to the desktop environment, the Proximity System is a cross-platform Java application for Windows, OSX, and Linux systems, which has been tested on Windows 7 and Debian Linux using the Sun Java 6 Runtime. In terms of the implementation of the theoretical approaches, both the Android and the desktop based applications use the same back-end libraries to perform the description-based calculations, where the only differences are the user interface and the Android version has less available features due to restrictions on system resources.
See also[edit]
Notes[edit]
- ^ J.R. Isbell observed that the notions near and far are important in a uniform space. Sets are far (uniformaly distal), provided the is a discrete collection. A nonempty set is a uniform neighbourhood of a set , provided the complement of is far from . See, §33 in [23]
- ^ The intuition that led to the discovery of descriptively near sets is given in Pawlak, Z.;Peters, J.F. (2002, 2007) "Jak blisko (How Near)". Systemy Wspomagania Decyzji I 57 (109)
- ^
- ^ Reminiscent of M. Pavel's approach, descriptions of members of sets objects are defined relative to vectors of values obtained from real-valued functions called probes. See, Pavel, M. (1993). Fundamentals of pattern recognition. 2nd ed. New York: Marcel Dekker, for the introduction of probe functions considered in the context of image registration.
- ^ A non-spatial view of near sets appears in, C.J. Mozzochi, M.S. Gagrat, and S.A. Naimpally, Symmetric generalized topological structures, Exposition Press, Hicksville, NY, 1976., and, more recently, nearness of disjoint sets and based on resemblance between pairs of elements (i.e. and have similar feature vectors and the norm ) See, e.g.,[43][42][53].
- ^
- ^ Observe that up to the 1970s, proximity meant EF-proximity, since this is the one that was studied intensively. The pre-1970 work on proximity spaces is exemplified by the series of papers by J. M. Smirnov during the first half of the 1950s[68][67][69][70], culminating in the compendious collection of results by S.A. Naimpally and B.D. Warrack[34]. But in view of later developments, there is a need to distinguish between various proximities. A basic proximity or Čech-proximity was introduced by E. Čech during the late 1930s (see §25 A.1, pp. 439-440 in [78]). The conditions for the non-symmetric case for a proximity were introduced by S. Leader[28] and for the symmetric case by M.W. Lodato[29][30][31].
References[edit]
- ^ Adámek, J.; Herrlich, H.; Strecker, G. E. (1990). Abstract and concrete categories. London: Wiley-Interscience. pp. ix+482.
- ^ Beer, G. (1993). Topologies on closed and closed convex sets. London, UK: Kluwer Academic Pub.
- ^ Bentley, H. L.; Colebunders, E.; Vandermissen, E. (2009). "A convenient setting for completions and function spaces". In Mynard, F.; Pearl, E. (eds.). Beyond Topology. Contemporary Mathematics. Providence, RI: American Mathematical Society. pp. 37–88.
- ^ Cameron, P.; Hockingand, J. G.; Naimpally, S. A. (1974). "Nearness–a better approach to continuity and limits". American Mathematical Monthly. 81 (7): 739–745. doi:10.2307/2319561. JSTOR 2319561.
- ^ Di Concilio, A. (2008). "Action, uniformity and proximity". In Naimpally, S. A.; Di Maio, G. (eds.). Theory and Applications of Proximity, Nearness and Uniformity. Seconda Università di Napoli, Napoli: Prentice-Hall. pp. 71–88.
- ^ a b Di Concilio, Anna (2009). "Proximity: a powerful tool in extension theory, function spaces, hyperspaces, Boolean algebras and point-free geometry". Beyond topology. Contemporary Mathematics. Vol. 486. Providence, RI: American Mathematical Society. pp. 89–114. doi:10.1090/conm/486/09508. ISBN 9780821842799. MR 2521943.
- ^ Devi, R.; Selvakumar, A.; Vigneshwaran, M. (2010). "-generalized semi-closed sets in topological spaces". Filomat. 24 (1): 97–100. CiteSeerX 10.1.1.430.5991. doi:10.2298/fil1001097d.
- ^ a b c Efremovič, V. A. (1952). "The geometry of proximity I (in Russian)". Matematicheskii Sbornik. Novaya Seriya. 31(73) (1): 189–200.
- ^ Peters, J. F. (2008). "A note on a-open sets and e-sets". Filomat. 22 (1): 89–96. doi:10.2298/FIL0801087E.
- ^ Fechner, G. T. (1966). Elements of Psychophysics, vol. I. London, UK: Hold, Rinehart & Winston. pp. H. E. Adler's trans. of Elemente der Psychophysik, 1860.
- ^ Fréchet, M. (1906). "Sur quelques points du calcul fonctionnel". Rend. Circ. Mat. Palermo. 22: 1–74. doi:10.1007/bf03018603. hdl:10338.dmlcz/100655. S2CID 123251660.
- ^ Grätzer, G.; Wenzel, G. H. (1989). "Tolerances, covering systems, and the axiom of choice". Archivum Mathematicum. 25 (1–2): 27–34.
- ^ Gupta, S.; Patnaik, K. (2008). "Enhancing performance of face recognition systems by using near set approach for selecting facial features". Journal of Theoretical and Applied Information Technology. 4 (5): 433–441.
- ^ a b Hassanien, A. E.; Abraham, A.; Peters, J. F.; Schaefer, G.; Henry, C. (2009). "Rough sets and near sets in medical imaging: A review". IEEE Transactions on Information Technology in Biomedicine. 13 (6): 955–968. CiteSeerX 10.1.1.475.6138. doi:10.1109/TITB.2009.2017017. PMID 19304490. S2CID 1262076.
- ^ Hausdorff, F. (1914). Grundz¨uge der mengenlehre. Leipzig: Veit and Company. pp. viii + 476.
- ^ Henry, C.; Peters, J. F. (2010). "Perception-based image classification, International". International Journal of Intelligent Computing and Cybernetics. 3 (3): 410–430. doi:10.1108/17563781011066701. S2CID 24382697.
- ^ a b c d
- ^ a b Henry, C.; Peters, J. F. (2011). "Arthritic hand-finger movement similarity measurements: Tolerance near set approach". Computational and Mathematical Methods in Medicine. 2011: 569898. doi:10.1155/2011/569898. PMC 3087412. PMID 21559241.
- ^ Henry, C. J.; Ramanna, S. (2011). "Parallel Computation in Finding Near Neighbourhoods". Rough Sets and Knowledge Technology. Lecture Notes in Computer Science. Vol. 6954. pp. 523–532. doi:10.1007/978-3-642-24425-4_67. ISBN 978-3-642-24424-7.
- ^ a b Herrlich, H. (1974). "A concept of nearness". General Topology and Its Applications. 4 (3): 191–212. doi:10.1016/0016-660x(74)90021-x.
- ^ Hocking, J. G.; Naimpally, S. A. (2009). "Nearness—a better approach to continuity and limits". Uniformity and Proximity. Allahabad Mathematical Society Lecture Note Series. Vol. 3. Allahabad: The Allahabad Mathematical Society. pp. iv+66. ISBN 978-81-908159-1-8.
- ^ Ïnan, E.; Öztürk, M. A. (2012). "Near groups on nearness approximation spaces". Hacettepe Journal of Mathematics and Statistics. 41 (4): 545–558.
- ^ Isbell, J. R. (1964). Uniform spaces. Providence, Rhode Island: American Mathematical Society. pp. xi + 175.
- ^ Ivanova, V. M.; Ivanov, A. A. (1959). "Contiguity spaces and bicompact extensions of topological spaces (russian)". Dokl. Akad. Nauk SSSR. 127: 20–22.
- ^ Knaster, B.; Kuratowski, C. (1921). "Sur les ensembles connexes". Fundamenta Mathematicae. 2: 206–255. doi:10.4064/fm-2-1-206-255.
- ^
- ^ Kuratowski, C. (1958). Topologie i. Warsaw: Panstwowe Wydawnictwo Naukowe.
- ^ Leader, S. (1967). "Metrization of proximity spaces". Proceedings of the American Mathematical Society. 18 (6): 1084–1088. doi:10.2307/2035803. JSTOR 2035803.
- ^ Lodato, M. W. (1962). On topologically induced generalized proximity relations (doctoral dissertation). Rutgers University.
- ^ Lodato, M. W. (1964). "On topologically induced generalized proximity relations I". Proceedings of the American Mathematical Society. 15 (3): 417–422. doi:10.2307/2034517. JSTOR 2034517.
- ^ Lodato, M. W. (1966). "On topologically induced generalized proximity relations II". Pacific Journal of Mathematics. 17: 131–135. doi:10.2140/pjm.1966.17.131.
- ^ MacLane, S. (1971). Categories for the working mathematician. Berlin: Springer. pp. v+262pp.
- ^ Mozzochi, C. J.; Naimpally, S. A. (2009). "Uniformity and proximity". Uniformity and Proximity. Allahabad Mathematical Society Lecture Note Series. Vol. 2. Allahabad: The Allahabad Mathematical Society. pp. xii+153. ISBN 978-81-908159-1-8.
- ^ Naimpally, S. A. (1970). Proximity spaces. Cambridge, UK: Cambridge University Press. pp. x+128. ISBN 978-0-521-09183-1.
- ^ Naimpally, S. A. (2009). Proximity approach to problems in topology and analysis. Munich, Germany: Oldenbourg Verlag. pp. ix + 204. ISBN 978-3-486-58917-7.
- ^ Naimpally, S. A.; Peters, J. F. (2013). "Preservation of continuity". Scientiae Mathematicae Japonicae. 76 (2): 1–7.
- ^ a b c d Naimpally, S. A.; Peters, J. F. (2013). Topology with Applications. Topological Spaces via Near and Far. Singapore: World Scientific.
- ^ Naimpally, S. A.; Peters, J. F.; Wolski, M. (2013). Near set theory and applications. Special Issue in Mathematics in Computer Science. Vol. 7. Berlin: Springer. p. 136.
- ^ Naimpally, S. A.; Warrack, B. D. (1970). Proximity spaces. Cambridge Tracts in Mathematics. Vol. 59. Cambridge, UK: Cambridge University Press.
- ^ Pal, S. K.; Peters, J. F. (2010). Rough fuzzy image analysis. Foundations and methodologies. London, UK: CRC Press, Taylor & Francis Group. ISBN 9781439803295.
- ^ Peters, J. F. (2009). "Tolerance near sets and image correspondence". International Journal of Bio-Inspired Computation. 1 (4): 239–245. doi:10.1504/ijbic.2009.024722.
- ^ a b c Peters, J. F.; Wasilewski, P. (2009). "Foundations of near sets". Information Sciences. 179 (18): 3091–3109. doi:10.1016/j.ins.2009.04.018.
- ^ a b c Peters, J. F. (2007). "Near sets. General theory about nearness of objects". Applied Mathematical Sciences. 1 (53): 2609–2629.
- ^ a b Peters, J. F. (2007). "Near sets. Special theory about nearness of objects". Fundamenta Informaticae. 75 (1–4): 407–433.
- ^ Peters, J. F. (2010). "Corrigenda and addenda: Tolerance near sets and image correspondence". International Journal of Bio-Inspired Computation. 2 (5): 310–318. doi:10.1504/ijbic.2010.036157.
- ^ Peters, J. F. (2011). "How near are Zdzisław Pawlak's paintings? Merotopic distance between regions of interest". In Skowron, A.; Suraj, S. (eds.). Rough Sets and Intelligent Systems – Professor Zdzisław Pawlak in Memoriam. Intelligent Systems Reference Library. Vol. 42. Berlin: Springer. pp. 1–19.
- ^ Peters, J. F. (2011). "Sufficiently near sets of neighbourhoods". In Yao, J. T.; Ramanna, S.; Wang, G.; Suraj, Z. (eds.). Rough Set and Knowledge Technology: 6th International Conference, RSKT 2011, Banff, Canada, October 9-12, 2011, Proceedings. Lecture Notes in Artificial Intelligence. Vol. 6954. Berlin: Springer. pp. 17–24. doi:10.1007/978-3-642-24425-4_4.
- ^ a b c d Peters, J. F. (2013). "Near sets: An introduction". Mathematics in Computer Science. 7 (1): 3–9. doi:10.1007/s11786-013-0149-6. S2CID 1573876.
- ^ a b c Peters, J. F. (2014). "Proximal relator spaces". Filomat: 1–5 (in press).
- ^ a b c d e Peters, J. F. (2014). Topology of Digital Images. Visual Pattern Discovery in Proximity Spaces. Vol. 63. Springer. p. 342. ISBN 978-3-642-53844-5.
- ^ a b Peters, J. F.; İnan, E.; Öztürk, M. A. (2014). "Spatial and descriptive isometries in proximity spaces". General Mathematics Notes. 21 (2): 125–134.
- ^ Peters, J. F.; Naimpally, S. A. (2011). "Approach spaces for near families". General Mathematics Notes. 2 (1): 159–164.
- ^ a b c Peters, J. F.; Naimpally, S. A. (2011). "Approach spaces for near families" (PDF). General Mathematics Notes. 2 (1): 159–164.
- ^ Peters, J. F.; Puzio, L. (2009). "Image analysis with anisotropic wavelet-based nearness measures". International Journal of Computational Intelligence Systems. 2 (3): 168–183. doi:10.1016/j.ins.2009.04.018.
- ^ Peters, J. F.; Shahfar, S.; Ramanna, S.; Szturm, T. (2007). "Biologically-inspired adaptive learning: A near set approach". IEEE Frontiers in the Convergence of Bioscience and Information Technology (FBIT 2007), Jeju Island, Korea, 11-13 Oct. 2007.
- ^ Peters, J. F.; Tiwari, S. (2011). "Approach merotopies and near filters. Theory and application". General Mathematics Notes. 3 (1): 32–45.
- ^ Peters, J. F.; Tiwari, S. (2011). "Approach merotopies and near filters. Theory and application". General Mathematics Notes. 3 (1): 32–45.
- ^ Peters, J. F.; Wasilewski, P. (2012). "Tolerance spaces: Origins, theoretical aspects and applications". Information Sciences. 195: 211–225. doi:10.1016/j.ins.2012.01.023.
- ^ Picado, J. "Weil nearness spaces". Portugaliae Mathematica. 55 (2): 233–254.
- ^ a b c Poincaré, J. H. (1895). "L'espace et la géomètrie". Revue de Métaphysique et de Morale. 3 (6): 631–646.
- ^ a b c Poincaré, J. H. (1902). "Sur certaines surfaces algébriques; troisième complément 'a l'analysis situs". Bulletin de la Société Mathématique de France. 30: 49–70. doi:10.24033/bsmf.657.
- ^ a b Poincaré, J. H. (2009) [1913]. Dernières pensées, trans. by J.W. Bolduc as Mathematics and science: Last essays. Paris & NY: Flammarion & Kessinger.
- ^ a b Poincaré, J. H. (1894). "Sur la nature du raisonnement mathématique". Revue de Métaphysique et de Morale. 2 (4): 371–384.
- ^ a b Ramanna, S.; Meghdadi, A. H. (2009). "Measuring resemblances between swarm behaviours: A perceptual tolerance near set approach". Fundamenta Informaticae. 95 (4): 533–552. doi:10.3233/FI-2009-163.
- ^ a b Riesz, F. (1908). "Stetigkeitsbegriff und abstrakte mengenlehre" (PDF). Atti del IV Congresso Internazionale dei Matematici II: 18–24.
- ^ Shreider, J. A. (1975). Equality, resemblance, and order. Russia: Mir Publishers. p. 279.
- ^ a b c d Smirnov, J. M. (1952). "On proximity spaces". Matematicheskii Sbornik. Novaya Seriya. 31(73) (3): 543–574. (English translation: Amer. Math. Soc. Trans. Ser. 2, 38, 1964, 5–35)
- ^ Smirnov, J. M. (1952). "On proximity spaces in the sense of V.A. Efremovič". Matematicheskii Sbornik. Novaya Seriya. 84: 895–898. English translation: Amer. Math. Soc. Trans. Ser. 2, 38, 1964, 1–4
- ^ Smirnov, J. M. (1954). "On the completeness of proximity spaces. I.". Trudy Moskov. Mat. Obšč. 3: 271–306, English translation: Amer. Math. Soc. Trans. Ser. 2, 38, 1964, 37–74.
- ^ Smirnov, J. M. (1955). "On the completeness of proximity spaces. II". Trudy Moskov. Mat. Obšč. 4: 421–438, English translation: Amer. Math. Soc. Trans. Ser. 2, 38, 1964, 75–94.
- ^ a b Sossinsky, A. B. (1986). "Tolerance space theory and some applications". Acta Applicandae Mathematicae. 5 (2): 137–167. doi:10.1007/bf00046585. S2CID 119731847.
- ^ Száz, Á. (1997). "Uniformly, proximally and topologically compact relators". Mathematica Pannonica. 8 (1): 103–116.
- ^ Száz, Á. (1987). "Basic tools and mild continuities in relator spaces". Acta Mathematica Hungarica. 50 (3–4): 177–201. doi:10.1007/bf01903935. S2CID 122231880.
- ^ Száz, Á (2000). "An extension of Kelley's closed relation theorem to relator spaces". Filomat. 14: 49–71.
- ^ Tiwari, S. (2010). Some aspects of general topology and applications. Approach merotopic structures and applications (doctoral dissertation). Dept. Of Math., Allahabad (U.P.), India.
- ^ a b Tiwari, S.; Peters, J. F. (2013). "A new approach to the study of extended metric spaces". Mathematica Aeterna. 3 (7): 565–577.
- ^ Tukey, J. W. (1940). Convergence and uniformity in topology. Annals of Mathematics Studies. Vol. AM-2. Princeton, NJ: Princeton Univ. Press. p. 90.
- ^ Čech, E. (1966). Topological spaces, revised ed. by Z. Frolik and M. Katětov. London: John Wiley & Sons. p. 893.
- ^ Wasilewski, P. (2004). On selected similarity relations and their applications into cognitive science (doctoral dissertation). Dept. Logic.
- ^ Wasilewski, P.; Peters, J. F.; Ramanna, S. (2011). "Perceptual Tolerance Intersection". Transactions on Rough Sets XIII. Lecture Notes in Computer Science. Vol. 6499. pp. 159–174. Bibcode:2011LNCS.6499..159W. doi:10.1007/978-3-642-18302-7_10. ISBN 978-3-642-18301-0.
- ^ Weil, A. (1938). Sur les espaces à structure uniforme et sur la topologie générale. Actualités scientifique et industrielles. Paris: Harmann & cie.
- ^ Wolski, M. (2010). "Perception and classification. A note on near sets and rough sets". Fundamenta Informaticae. 101 (1–2): 143–155. doi:10.3233/FI-2010-281.
- ^ a b Zeeman, E. C. (1962). "The topology of the brain and visual perception". In Fort, Jr., M. K. (ed.). Topology of 3-Manifolds and Related Topics. University of Georgia Institute Conference Proceedings. Prentice-Hall. pp. 240–256.
Further reading[edit]
- Naimpally, S. A.; Peters, J. F. (2013). Topology with Applications. Topological Spaces via Near and Far. World Scientific Publishing . Co. Pte. Ltd. ISBN 978-981-4407-65-6.
- Naimpally, S. A.; Peters, J. F.; Wolski, M. (2013). Near Set Theory and Applications. Mathematics in Computer Science. Vol. 7. Berlin: Springer.
- Peters, J. F. (2014). Topology of Digital Images. Visual Pattern Discovery in Proximity Spaces. Intelligent Systems Reference Library. Vol. 63. Berlin: Springer.
- Henry, C. J.; Peters, J. F. (2012). Near set evaluation and recognition (NEAR) system V3.0. UM CI Laboratory Technical Report No. TR-2009-015. Computational Intelligence Laboratory, University of Manitoba.
- Concilio, A. Di (2014). Proximity: A powerful tool in extension theory, function spaces, hyperspaces, boolean algebras and point-free geometry. UM CI Laboratory Technical Report No. TR-2009-021. Computational Intelligence Laboratory, University of Manitoba.
- Peters, J. F.; Naimpally, S. A. (2012). "Applications of near sets" (PDF). Notices of the American Mathematical Society. 59 (4): 536–542. CiteSeerX 10.1.1.371.7903. doi:10.1090/noti817.



















![{\displaystyle D_{\rho }:2^{X}\times 2^{X}\longrightarrow [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd3912d3d822f136a057b2da80922c93c6a02753)
































































































































![{\displaystyle \varepsilon \in (0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b8823762ca4029df1472e0fe9e7efb5033a73be)






































![{\displaystyle D_{_{tNM}}:2^{U}\times 2^{U}:\longrightarrow [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f36803649c5170abb7500f39c6f8be8bb462ea5)









