Pentagonal prism
| Uniform pentagonal prism | |
|---|---|

| |
| Type | Prismatic uniform polyhedron |
| Elements | F = 7, E = 15 V = 10 (χ = 2) |
| Faces by sides | 5{4}+2{5} |
| Schläfli symbol | t{2,5} or {5}×{} |
| Wythoff symbol | 2 5 | 2 |
| Coxeter diagram | |
| Symmetry group | D5h, [5,2], (*522), order 20 |
| Rotation group | D5, [5,2]+, (522), order 10 |
| References | U76(c) |
| Dual | Pentagonal dipyramid |
| Properties | convex |
 Vertex figure 4.4.5 | |

In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with seven faces, fifteen edges, and ten vertices.
As a semiregular (or uniform) polyhedron[edit]
If faces are all regular, the pentagonal prism is a semiregular polyhedron, more generally, a uniform polyhedron, and the third in an infinite set of prisms formed by square sides and two regular polygon caps. It can be seen as a truncated pentagonal hosohedron, represented by Schläfli symbol t{2,5}. Alternately it can be seen as the Cartesian product of a regular pentagon and a line segment, and represented by the product {5}×{}. The dual of a pentagonal prism is a pentagonal bipyramid.
The symmetry group of a right pentagonal prism is D5h of order 20. The rotation group is D5 of order 10.
Volume[edit]
The volume, as for all prisms, is the product of the area of the pentagonal base times the height or distance along any edge perpendicular to the base. For a uniform pentagonal prism with edges h the formula is
Use[edit]
Nonuniform pentagonal prisms called pentaprisms are also used in optics to rotate an image through a right angle without changing its chirality.
In 4-polytopes[edit]
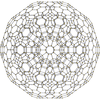
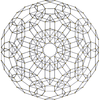
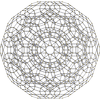
It exists as cells of four nonprismatic uniform 4-polytopes in four dimensions:
| cantellated 600-cell |
cantitruncated 600-cell |
runcinated 600-cell |
runcitruncated 600-cell |

|
|
|
|
Related polyhedra[edit]

The pentagonal stephanoid has pentagonal dihedral symmetry and has the same vertices as the uniform pentagonal prism.
| Family of uniform n-gonal prisms | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prism name | Digonal prism | (Trigonal) Triangular prism |
(Tetragonal) Square prism |
Pentagonal prism | Hexagonal prism | Heptagonal prism | Octagonal prism | Enneagonal prism | Decagonal prism | Hendecagonal prism | Dodecagonal prism | ... | Apeirogonal prism |
| Polyhedron image | ... | ||||||||||||
| Spherical tiling image | Plane tiling image | ||||||||||||
| Vertex config. | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | ... | ∞.4.4 |
| Coxeter diagram | ... | ||||||||||||
External links[edit]
- Weisstein, Eric W. "Pentagonal prism". MathWorld.
- Pentagonal Prism Polyhedron Model -- works in your web browser


