Polyhex (mathematics)

In recreational mathematics, a polyhex is a polyform with a regular hexagon (or 'hex' for short) as the base form, constructed by joining together 1 or more hexagons. Specific forms are named by their number of hexagons: monohex, dihex, trihex, tetrahex, etc. They were named by David Klarner who investigated them.
Each individual polyhex tile and tessellation polyhexes and can be drawn on a regular hexagonal tiling.
Construction rules[edit]
The rules for joining hexagons together may vary. Generally, however, the following rules apply:
- Two hexagons may be joined only along a common edge, and must share the entirety of that edge.
- No two hexagons may overlap.
- A polyhex must be connected. Configurations of disconnected basic polygons do not qualify as polyhexes.
- The mirror image of an asymmetric polyhex is not considered a distinct polyhex (polyhex are "double sided").
Tessellation properties[edit]

All of the polyhexes with fewer than five hexagons can form at least one regular plane tiling.
In addition, the plane tilings of the dihex and straight polyhexes are invariant under 180 degrees rotation or reflection parallel or perpendicular to the long axis of the dihex (order 2 rotational and order 4 reflection symmetry), and the hexagon tiling and some other polyhexes (like the hexahex with one hole, below) are invariant under 60, 120 or 180 degree rotation (order 6 rotational and reflection symmetry).
In addition, the hexagon is a hexiamond, so all polyhexes are also distinct polyiamonds. Also, as an equilateral triangle is a hexagon and three smaller equilateral triangles it is possible to superimpose a large polyiamond on any polyhex, giving two polyiamonds corresponding to each polyhex. This is used as the basis of an infinite division of a hexagon into smaller and smaller hexagons (an irrep-tiling) or into hexagons and triangles.
Enumeration[edit]



As with polyominoes, polyhexes may be enumerated as free polyhexes (where rotations and reflections count as the same shape), fixed polyhexes (where different orientations count as distinct) and one-sided polyhexes (where mirror images count as distinct but rotations count as identical). They may also be distinguished according to whether they may contain holes. The number of free n-hexes for n = 1, 2, 3, … is 1, 1, 3, 7, 22, 82, 333, 1448, … (sequence A000228 in the OEIS); the number of free polyhexes with holes is given by OEIS: A038144; the number of free polyhexes without holes is given by OEIS: A018190; the number of one-sided polyhexes is given by OEIS: A006535; the number of fixed polyhexes is given by OEIS: A001207.[1][2]
| n | Free | Free with holes | Free without holes | One-sided | Fixed |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0 | 1 | 1 | 3 |
| 3 | 3 | 0 | 3 | 3 | 11 |
| 4 | 7 | 0 | 7 | 10 | 44 |
| 5 | 22 | 0 | 22 | 33 | 186 |
| 6 | 82 | 1 | 81 | 147 | 814 |
| 7 | 333 | 2 | 331 | 620 | 3652 |
| 8 | 1448 | 13 | 1435 | 2821 | 16689 |
| 9 | 6572 | 67 | 6505 | 12942 | 77359 |
| 10 | 30490 | 404 | 30086 | 60639 | 362671 |
Symmetry[edit]
Of the polyhexes up to hexahexes, 2 have 6-fold rotation and reflection symmetry (thus also 3-fold and 2-fold symmetry), the monohex and the hexahex with a hole, 3 others have 3-fold rotation (the compact trihex, the propeller tetrahex and the hexahex looking like an equilateral triangle) and 3-fold reflection symmetry, 9 others have 2-fold rotation and reflection, 8 have just two fold rotation, 16 just have 2-fold reflection and the other 78 (most of the tetrahexes, pentahexes or hexahexes) are asymmetrical. The tilings of most of the reflection-symmetrical polyhexes are also invariant under glide reflections of the same order by the length of the polyhex.
Monohexes[edit]
There is one monohex. It tiles the plane as a regular hexagonal tiling.
Dihexes[edit]
There is one free dihex:
Trihexes[edit]
There are 3 free and two-sided trihexes:
Tetrahexes[edit]
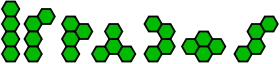
There are 7 free and two-sided tetrahexes. They are given names, in the order shown: bar, worm, pistol, propeller, arch, bee, and wave.[3]
Pentahexes[edit]
There are 22 free and two-sided pentahexes:
Hexahexes[edit]
There are 82 free and two-sided hexahexes:
See also[edit]
- Tessellation
- Percolation theory
- Polyiamond – tilings with equilateral triangles
- Polyomino – tilings with squares
- Polycyclic aromatic hydrocarbon – hydrocarbons whose structure is based on polyhexes
- Rep-tile – tilings of shapes that are made of smaller copies of themselves
References[edit]
- ^ Wolfram Mathworld: Polyhex
- ^ Glenn C. Rhoads, Planar tilings by polyominoes, polyhexes, and polyiamonds, Journal of Computational and Applied Mathematics 174 (2005), No. 2, pp 329–353
- ^ Gardner, M. Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, p. 147, 1978. PDF