Thermal radiation

Thermal radiation is electromagnetic radiation emitted by the thermal motion of particles in matter. Thermal radiation transmits as an electromagnetic wave through both matter and vacuum. When matter absorbs thermal radiation its temperature will tend to rise. All matter with a temperature greater than absolute zero emits thermal radiation. The emission of energy arises from a combination of electronic, molecular, and lattice oscillations in a material.[1] Kinetic energy is converted to electromagnetism due to charge-acceleration or dipole oscillation. At room temperature, most of the emission is in the infrared (IR) spectrum.[2]: 73–86 Thermal radiation is one of the fundamental mechanisms of heat transfer, along with conduction and convection.
The primary method by which the Sun transfers heat to the Earth is thermal radiation. This energy is partially absorbed and scattered in the atmosphere, the latter process being the reason why the sky is visibly blue.[3] Much of the Sun's radiation transmits through the atmosphere to the surface where it is either absorbed or reflected.
Thermal radiation can be used to detect objects or phenomena normally invisible to the human eye. Thermographic cameras create an image by sensing infrared radiation. These images can represent the temperature gradient of a scene and are commonly used to locate objects at a higher temperature than their surroundings. In a dark environment where visible light is at low levels, infrared images can be used to locate animals or people due to their body temperature. Cosmic microwave background radiation is another example of thermal radiation.
Blackbody radiation is a concept used to analyze thermal radiation in idealized systems. This model applies if a radiation object meets the physical characteristics of a black body in thermodynamic equilibrium.[4]: 278 Planck's law describes the spectrum of blackbody radiation, and relates the radiative heat flux from a body to its temperature. Wien's displacement law determines the most likely frequency of the emitted radiation, and the Stefan–Boltzmann law gives the radiant intensity.[4]: 280 Where blackbody radiation is not an accurate approximation, emission and absorption can be modeled using quantum electrodynamics (QED).[1]
Overview[edit]
Thermal radiation is the emission of electromagnetic waves from all matter that has a temperature greater than absolute zero.[5][2] Thermal radiation reflects the conversion of thermal energy into electromagnetic energy. Thermal energy is the kinetic energy of random movements of atoms and molecules in matter. It is present in all matter of nonzero temperature. These atoms and molecules are composed of charged particles, i.e., protons and electrons. The kinetic interactions among matter particles result in charge acceleration and dipole oscillation. This results in the electrodynamic generation of coupled electric and magnetic fields, resulting in the emission of photons, radiating energy away from the body. Electromagnetic radiation, including visible light, will propagate indefinitely in vacuum.

The characteristics of thermal radiation depend on various properties of the surface from which it is emanating, including its temperature and its spectral emissivity, as expressed by Kirchhoff's law.[5] The radiation is not monochromatic, i.e., it does not consist of only a single frequency, but comprises a continuous spectrum of photon energies, its characteristic spectrum. If the radiating body and its surface are in thermodynamic equilibrium and the surface has perfect absorptivity at all wavelengths, it is characterized as a black body. A black body is also a perfect emitter. The radiation of such perfect emitters is called black-body radiation. The ratio of any body's emission relative to that of a black body is the body's emissivity, so a black body has an emissivity of one.
Absorptivity, reflectivity, and emissivity of all bodies are dependent on the wavelength of the radiation. Due to reciprocity, absorptivity and emissivity for any particular wavelength are equal at equilibrium – a good absorber is necessarily a good emitter, and a poor absorber is a poor emitter. The temperature determines the wavelength distribution of the electromagnetic radiation.
The distribution of power that a black body emits with varying frequency is described by Planck's law. At any given temperature, there is a frequency fmax at which the power emitted is a maximum. Wien's displacement law, and the fact that the frequency is inversely proportional to the wavelength, indicates that the peak frequency fmax is proportional to the absolute temperature T of the black body. The photosphere of the sun, at a temperature of approximately 6000 K, emits radiation principally in the (human-)visible portion of the electromagnetic spectrum. Earth's atmosphere is partly transparent to visible light, and the light reaching the surface is absorbed or reflected. Earth's surface emits the absorbed radiation, approximating the behavior of a black body at 300 K with spectral peak at fmax. At these lower frequencies, the atmosphere is largely opaque and radiation from Earth's surface is absorbed or scattered by the atmosphere. Though about 10% of this radiation escapes into space, most is absorbed and then re-emitted by atmospheric gases. It is this spectral selectivity of the atmosphere that is responsible for the planetary greenhouse effect, contributing to global warming and climate change in general (but also critically contributing to climate stability when the composition and properties of the atmosphere are not changing).
History[edit]
Ancient Greece[edit]
Burning glasses are known to date back to about 700 BC. One of the first accurately mentions of burning glasses appears in Aristophanes's comedy, The Clouds, written in 423 BC.[6] According to the Archimedes' heat ray anecdote, Archimedes is purported to have developed mirrors to concentrate heat rays in order to burn attacking Roman ships during the Siege of Syracuse (c. 213–212 BC), but no sources from the time have been confirmed.[6] Catoptrics is a book attributed to Euclid on how to focus light in order to produce heat, but the book might have been written in 300 AD.[6]
Renaissance[edit]
During the same period, Santorio Santorio came up with one of the earliest thermoscopes. In 1612 he published his results on the heating effects from the Sun, and attempts to measure heat from the Moon.[6]
Earlier 1589, Giambattista della Porta reported on the heat resented by his face, emitted by a remote candle and facilitated by a concave metallic mirror. He also reported the cooling felt from a solid ice block[6] Della Porta experiment would be replicated many times with increasing accuracy. It was replicated by astronomers Giovanni Antonio Magini and Christopher Heydon in 1603, and supplied instructions for Rudolf II, Holy Roman Emperor who performed it in 1611. In 1660, della Porta experiment was updated by the Accademia del Cimento using a thermometer invented by Ferdinand II, Grand Duke of Tuscany.[6]
Enlightenment[edit]
In 1761, Benjamin Franklin wrote a letter describing his experiments on the relationship between color and heat absorption.[7] He found that darker color clothes got hotter when exposed to sunlight than lighter color clothes. One experiment he performed consisted of placing square pieces of cloth of various color out in the snow on a sunny day. He waited some time and then measured that the black pieces sank furthest into the snow of all the colors, indicating that they got the hottest and melted the most snow.
Caloric theory[edit]
Antoine Lavoisier considered that radiation of heat was concerned with the condition of the surface of a physical body rather than the material of which it was composed.[8] Lavoisier described a poor radiator to be a substance with a polished or smooth surface as it possessed its molecules lying in a plane closely bound together thus creating a surface layer of caloric fluid which insulated the release of the rest within.[8] He described a great radiator to be a substance with a rough surface as only a small amount of molecules held caloric in within a given plane allowing for greater escape from within.[8] Count Rumford would later cite this explanation of caloric movement as insufficient to explain the radiation of cold becoming a point of contention for the theory as a whole.[8]
In his first memoir, Augustin-Jean Fresnel responded to a view he extracted from a French translation of Isaac Newton's Optics. He says that Newton imagined particles of light traversing space uninhibited by the caloric medium filling it, and refutes this view (never actually held by Newton) by saying that a body under illumination would increase indefinitely in heat.[9]
In Marc-Auguste Pictet's famous experiment of 1790, it was reported that a thermometer detected a lower temperature when a set of mirror were used to focus "frigorific rays" from a cold object.[10]
In 1791, Pierre Prevost a colleague of Pictet, introduced the concept of radiative equilibrium, wherein all objects both radiates and absorb heat.[11] When an object is cooler than its surroundings, it absorbs more heat than it emits, causing its temperature to increase until it reaches equilibrium. Even at equilibrium, it continues to radiate heat, balancing absorption and emission.[11]
The discovery of infrared radiation is ascribed to astronomer William Herschel. Herschel published his results in 1800 before the Royal Society of London. Herschel used a prism to refract light from the sun and detected the calorific rays, beyond the red part of the spectrum, as an increase in the temperature recorded on a thermometer in that region.[12][13]
Aether theory[edit]
First, the earlier theory which originated from the concept of a hypothetical medium referred as aether. Ether supposedly fills all evacuated or non-evacuated spaces. The transmission of light or of radiant heat are allowed by the propagation of electromagnetic waves in the aether.[14] television and radio broadcasting waves are types of electromagnetic waves with specific wavelengths.[15] All electromagnetic waves travel at the same speed; therefore, shorter wavelengths are associated with high frequencies. Since every body or fluid is submerged in the ether, due to the vibration of the molecules, any body or fluid can potentially initiate an electromagnetic wave. All bodies generate and receive electromagnetic waves at the expense of its stored energy.[15]
In 1860, Gustav Kirchhoff published a mathematical description of thermal equilibrium (i.e. Kirchoff's law of thermal radiation).[16]: 275–301 By 1884 the emissive power of a perfect blackbody was inferred by Josef Stefan using John Tyndall's experimental measurements, and derived by Ludwig Boltzmann from fundamental statistical principles.[17] This relation is known as Stefan–Boltzmann law.
Quantum theory[edit]

The microscopic theory of radiation is best known as the quantum theory and was first offered by Max Planck in 1900.[14] According to this theory, energy emitted by a radiator is not continuous but is in the form of quanta. Planck noted that energy was emitted in quantas of frequency of vibration similarly to the wave theory.[18] The energy E an electromagnetic wave in vacuum is found by the expression E = hf, where h is the Planck constant and f is its frequency.
Bodies at higher temperatures emit radiation at higher frequencies with an increasing energy per quantum. While the propagation of electromagnetic waves of all wavelengths is often referred as "radiation", thermal radiation is often constrained to the visible and infrared regions. For engineering purposes, it may be stated that thermal radiation is a form of electromagnetic radiation which varies on the nature of a surface and its temperature.[14]
Radiation waves may travel in unusual patterns compared to conduction heat flow. Radiation allows waves to travel from a heated body through a cold non-absorbing or partially absorbing medium and reach a warmer body again.[14] An example is the case of the radiation waves that travel from the Sun to the Earth.
Characteristics[edit]
Emission[edit]
The radiation of heat is generally denoted by the word emission.[3]: 4 It is frequently described that surfaces "emit" radiation, however this is purely a simplification. According to the conservation of energy, emission always takes place at the expense of other forms of energy (electrical, chemical, etc.). Hence only material particles can emit heat, not geometrical volumes or surfaces. In reality, the radiation comes from the particles within a body and passes through its surfaces.
Propagation[edit]
The propagation of radiation in a medium that is assumed to be homogeneous, isotropic, and at rest takes place in straight lines and has the same velocity in all directions.[3]: 7–8 Unless if propagating through a vacuum, thermal radiation does decay over time as energy is scattered.
Scattering occurs due to the presence of discontinuities in every medium that arise from their atomic structure. An example of scattering is when thermal radiation from the sun scatters after entering the earth's atmosphere. On a clear day at noon, only about two-thirds of this radiation actually reaches the surface. The rest is intercepted by particles in the air and changed into heat in the process. Scattering is noticeably larger for rays of shorter wave length; hence the blue color of skylight.
Absorption, reflection, and transmission[edit]
When a heat ray arrives at a body they may interact in three different ways:
- The body may absorb the heat
- The body may reflect the heat
- The heat may transmit through the body
Absorption and reflection are typically modeled as surface phenomena that occur within a fraction of a micrometer of the surface.[19]: 801 For example, a highly polished piece of steel will be highly reflective, regardless of the material under the surface. Transmission on the other hand is a volumetric phenomena that is dependent on the properties of the entire thickness of the body. A glass window for instance must be translucent through its entire thickness for radiation to get through.
The term absorption is used to describe the change of heat into other forms of energy when it contacts particle or body.[3]: 11 Only material particles can absorb heat rays, not elements of surfaces. For a given frequency of radiation, all mediums have a coefficient of absorption, that represents how much heat will be absorbed per unit distance through a medium.
Reciprocity[edit]
The rate of electromagnetic radiation emitted at a given frequency is proportional to the amount of absorption that it would experience by the source, a property known as reciprocity. Thus, a surface that absorbs more red light thermally radiates more red light. This principle applies to all properties of the wave, including wavelength (color), direction, polarization, and even coherence. It is therefore possible to have thermal radiation which is polarized, coherent, and directional; though polarized and coherent forms are fairly rare in nature far from sources (in terms of wavelength).
Frequency[edit]
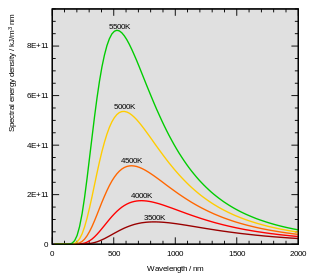
- Thermal radiation emitted by a body at any temperature consists of a wide range of frequencies. The frequency distribution is given by Planck's law of black-body radiation for an idealized emitter as shown in the diagram at top.
- The dominant frequency (or color) range of the emitted radiation shifts to higher frequencies as the temperature of the emitter increases. For example, a red hot object radiates mainly in the long wavelengths (red and orange) of the visible band. If it is heated further, it also begins to emit discernible amounts of green and blue light, and the spread of frequencies in the entire visible range cause it to appear white to the human eye; it is white hot. Even at a white-hot temperature of 2000 K, 99% of the energy of the radiation is still in the infrared. This is determined by Wien's displacement law. In the diagram the peak value for each curve moves to the left as the temperature increases.
| °C (°F) | Subjective color[20] |
|---|---|
| 480 °C (896 °F) | faint red glow |
| 580 °C (1,076 °F) | dark red |
| 730 °C (1,350 °F) | bright red, slightly orange |
| 930 °C (1,710 °F) | bright orange |
| 1,100 °C (2,010 °F) | pale yellowish orange |
| 1,300 °C (2,370 °F) | yellowish white |
| > 1,400 °C (2,550 °F) | white (yellowish if seen from a distance through atmosphere) |
Temperature[edit]
The total radiation intensity of a black body rises as the fourth power of the absolute temperature, as expressed by the Stefan–Boltzmann law. A kitchen oven, at a temperature about double room temperature on the absolute temperature scale (600 K vs. 300 K) radiates 16 times as much power per unit area. An object at the temperature of the filament in an incandescent light bulb—roughly 3000 K, or 10 times room temperature—radiates 10,000 times as much energy per unit area.
As for photon statistics, thermal light obeys Super-Poissonian statistics.
Fundamental principles[edit]
Thermal radiation is one of the three principal mechanisms of heat transfer. It entails the emission of a spectrum of electromagnetic radiation due to an object's temperature. Other mechanisms are convection and conduction.
Electromagnetic waves[edit]

Thermal radiation is characteristically different from conduction and convection in that it does not require a medium and, in fact it reaches maximum efficiency in a vacuum. Thermal radiation is a type of electromagnetic radiation which is often modeled by the propagation of waves. These waves have the standard wave properties of frequency, and wavelength, which are related by the equation
Irradiation[edit]
Thermal irradiation is the rate at which radiation is incident upon a surface per unit area.[19]: 771 It is measured in watts per square meter. Irradiation can either be reflected, absorbed, or transmitted. The components of irradiation can then be characterized by the equation
where, represents the absorptivity, reflectivity and transmissivity.[19]: 772 These components are a function of the wavelength of the electromagnetic wave as well as the material properties of the medium.
Absorptivity and emissivity[edit]
The spectral absorption is equal to the emissivity ; this relation is known as Kirchhoff's law of thermal radiation. An object is called a black body if this holds for all frequencies, and the following formula applies:
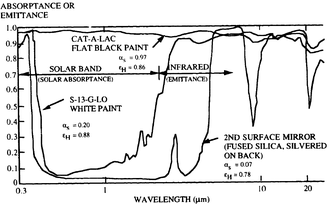
If objects appear white (reflective in the visual spectrum), they are not necessarily equally reflective (and thus non-emissive) in the thermal infrared – see the diagram at the left. Most household radiators are painted white, which is sensible given that they are not hot enough to radiate any significant amount of heat, and are not designed as thermal radiators at all – instead, they are actually convectors, and painting them matt black would make little difference to their efficacy. Acrylic and urethane based white paints have 93% blackbody radiation efficiency at room temperature[21] (meaning the term "black body" does not always correspond to the visually perceived color of an object). These materials that do not follow the "black color = high emissivity/absorptivity" caveat will most likely have functional spectral emissivity/absorptivity dependence.
Only truly gray systems (relative equivalent emissivity/absorptivity and no directional transmissivity dependence in all control volume bodies considered) can achieve reasonable steady-state heat flux estimates through the Stefan-Boltzmann law. Encountering this "ideally calculable" situation is almost impossible (although common engineering procedures surrender the dependency of these unknown variables and "assume" this to be the case). Optimistically, these "gray" approximations will get close to real solutions, as most divergence from Stefan-Boltzmann solutions is very small (especially in most standard temperature and pressure lab controlled environments).
Reflectivity[edit]
Reflectivity deviates from the other properties in that it is bidirectional in nature. In other words, this property depends on the direction of the incident of radiation as well as the direction of the reflection. Therefore, the reflected rays of a radiation spectrum incident on a real surface in a specified direction forms an irregular shape that is not easily predictable. In practice, surfaces are often assumed to reflect either in a perfectly specular or a diffuse manner. In a specular reflection, the angles of reflection and incidence are equal. In diffuse reflection, radiation is reflected equally in all directions. Reflection from smooth and polished surfaces can be assumed to be specular reflection, whereas reflection from rough surfaces approximates diffuse reflection.[14] In radiation analysis a surface is defined as smooth if the height of the surface roughness is much smaller relative to the wavelength of the incident radiation.
Transmissivity[edit]
A medium that experiences no transmission () is opaque, in which case absorptivity and reflectivity sum to unity:
Radiation intensity[edit]
Radiation emitted from a surface can propagate in any direction from the surface.[19]: 773 Irradiation can also be incident upon a surface from any direction. The amount of irradiation on a surface is therefore dependent on the relative orientation of both the emitter and the receiver. The parameter radiation intensity, is used to quantify how much radiation makes it from one surface to another.
Radiation intensity is often modeled using a spherical coordinate system.[19]: 773
Emissive power[edit]
Emissive power is the rate at which radiation is emitted per unit area.[19]: 776 It is a measure of heat flux. The total emissive power from a surface is denoted as and can be determined by,
The total emissive power can also be found by integrating the spectral emissive power over all possible wavelengths.[19]: 776 This is calculated as,
The spectral emissive power can also be determined from the spectral intensity, as follows,
Blackbody radiation[edit]
A "black body" is a body which has the property of allowing all incident rays to enter without surface reflection and not allowing them to leave again.[16]
Blackbodies are idealized surfaces that act as the perfect absorber and emitter.[19]: 782–783 They serve as the standard against which real surfaces are compared when characterizing thermal radiation. A blackbody is defined by three characteristics:
- A blackbody absorbs all incident radiation, regardless of wavelength and direction.
- No surface can emit more energy than a blackbody for a given temperature and wavelength.
- A blackbody is a diffuse emitter.
The Planck distribution[edit]
The spectral intensity of a blackbody, was first determined by Max Planck.[3] It is given by Planck's law per unit wavelength as:
The equation is derived as an infinite sum over all possible frequencies in a semi-sphere region. The energy, , of each photon is multiplied by the number of states available at that frequency, and the probability that each of those states will be occupied.
Stefan-Boltzmann law[edit]

The Planck distribution can be used to find the spectral emissive power of a blackbody, as follows,[19]: 784–785
The total emissive power of a blackbody is then calculated as,
Wien's displacment law[edit]
The wavelength for which the emission intensity is highest is given by Wien's displacement law as:
Constants[edit]
Definitions of constants used in the above equations:
| Symbol | Constant name | Value in SI units |
|---|---|---|
| Planck constant | 6.626 069 3(11)×10−34 J·s | |
| Wien's displacement constant | 2.897 768 5(51)×10−3 m·K | |
| Boltzmann constant | 1.380 650 5(24)×10−23 J·K−1 | |
| Stefan–Boltzmann constant | 5.670 373 (21)×10−8 W·m−2·K−4 | |
| Speed of light | 299 792 458 m·s−1 |
Variables[edit]
Definitions of variables, with example values:
| Absolute temperature | For units used above, must be in kelvins (e.g. average surface temperature on Earth = 288 K) | |
| Surface area | Acuboid = 2ab + 2bc + 2ac; Acylinder = 2π·r(h + r); Asphere = 4π·r2 |
Emission from non-black surfaces[edit]
For surfaces which are not black bodies, one has to consider the (generally frequency dependent) emissivity factor . This factor has to be multiplied with the radiation spectrum formula before integration. If it is taken as a constant, the resulting formula for the power output can be written in a way that contains as a factor:
This type of theoretical model, with frequency-independent emissivity lower than that of a perfect black body, is often known as a grey body. For frequency-dependent emissivity, the solution for the integrated power depends on the functional form of the dependence, though in general there is no simple expression for it. Practically speaking, if the emissivity of the body is roughly constant around the peak emission wavelength, the gray body model tends to work fairly well since the weight of the curve around the peak emission tends to dominate the integral.
Heat transfer between surfaces[edit]
Calculation of radiative heat transfer between groups of objects, including a 'cavity' or 'surroundings' requires solution of a set of simultaneous equations using the radiosity method. In these calculations, the geometrical configuration of the problem is distilled to a set of numbers called view factors, which give the proportion of radiation leaving any given surface that hits another specific surface. These calculations are important in the fields of solar thermal energy, boiler and furnace design and raytraced computer graphics.
The net radiative heat transfer from one surface to another is the radiation leaving the first surface for the other minus that arriving from the second surface.
- For black bodies, the rate of energy transfer from surface 1 to surface 2 is:
where is surface area, is energy flux (the rate of emission per unit surface area) and is the view factor from surface 1 to surface 2. Applying both the reciprocity rule for view factors, , and the Stefan–Boltzmann law, , yields:
- For two grey-body surfaces forming an enclosure, the heat transfer rate is:
Formulas for radiative heat transfer can be derived for more particular or more elaborate physical arrangements, such as between parallel plates, concentric spheres and the internal surfaces of a cylinder.[18]
Applications[edit]
Thermal radiation is an important factor of many engineering applications, especially for those dealing with high temperatures.
Solar energy[edit]
Electromagnetic radiation from the sun has a peak wavelength of about 550 nm.[1]

Concentrators[edit]
Thermal radiation can be concentrated on a tiny spot via reflecting mirrors, which concentrating solar power takes advantage of. Instead of mirrors, Fresnel lenses can also be used to concentrate radiant energy. In principle, any kind of lens can be used, but only the Fresnel lens design is practical for very large lenses. Either method can be used to quickly vaporize water into steam using sunlight. For example, the sunlight reflected from mirrors heats the PS10 Solar Power Plant, and during the day it can heat water to 285 °C (558 K; 545 °F).
Collectors[edit]
A selective surface can be used when energy is being extracted from the sun. Selective surfaces can also be used on solar collectors. We can find out how much help a selective surface coating is by looking at the equilibrium temperature of a plate that is being heated through solar radiation. If the plate is receiving a solar irradiation of 1350 W/m2 (minimum is 1325 W/m2 on 4 July and maximum is 1418 W/m2 on 3 January) from the sun the temperature of the plate where the radiation leaving is equal to the radiation being received by the plate is 393 K (248 °F). If the plate has a selective surface with an emissivity of 0.9 and a cut off wavelength of 2.0 μm, the equilibrium temperature is approximately 1250 K (1790 °F). The calculations were made neglecting convective heat transfer and neglecting the solar irradiation absorbed in the clouds/atmosphere for simplicity, the theory is still the same for an actual problem.
Incandescent light bulbs[edit]
The incandescent light bulb has a spectrum overlapping the black body spectra of the sun and the earth. Some of the photons emitted by a tungsten light bulb filament at 3000 K are in the visible spectrum. Most of the energy is associated with photons of longer wavelengths; these do not help a person see, but still transfer heat to the environment, as can be deduced empirically by observing an incandescent light bulb.
Thermal comfort[edit]

Thermal radiation plays a crucial role in human comfort, influencing perceived temperature sensation. Various technologies have been developed to enhance thermal comfort, including personal heating and cooling devices.
The mean radiant temperature is a metric used to quantify the exchange of radiant heat between a human and their surrounding environment.
Personal heating[edit]
Radiant personal heaters are devices that convert energy into infrared radiation that are designed to increase a user's perceived temperature. They typically are either gas-powered or electric. In domestic and commercial applications, gas-powered radiant heaters can produce a higher heat flux than electric heaters which are limited by the amount of current that can be drawn through a circuit breaker.
Personal cooling[edit]
Personalized cooling technology is an example of an application where optical spectral selectivity can be beneficial. Conventional personal cooling is typically achieved through heat conduction and convection. However, the human body is a very efficient emitter of infrared radiation, which provides an additional cooling mechanism. Most conventional fabrics are opaque to infrared radiation and block thermal emission from the body to the environment. Fabrics for personalized cooling applications have been proposed that enable infrared transmission to directly pass through clothing, while being opaque at visible wavelengths, allowing the wearer to remain cooler.
Windows[edit]
Low-emissivity windows in houses are a more complicated technology, since they must have low emissivity at thermal wavelengths while remaining transparent to visible light. To reduce the heat transfer from a surface, such as a glass window, a clear reflective film with a low emissivity coating can be placed on the interior of the surface. "Low-emittance (low-E) coatings are microscopically thin, virtually invisible, metal or metallic oxide layers deposited on a window or skylight glazing surface primarily to reduce the U-factor by suppressing radiative heat flow".[23] By adding this coating we are limiting the amount of radiation that leaves the window thus increasing the amount of heat that is retained inside the window.
Spacecraft[edit]
Shiny metal surfaces, have low emissivities both in the visible wavelengths and in the far infrared. Such surfaces can be used to reduce heat transfer in both directions; an example of this is the multi-layer insulation used to insulate spacecraft.
Since any electromagnetic radiation, including thermal radiation, conveys momentum as well as energy, thermal radiation also induces very small forces on the radiating or absorbing objects. Normally these forces are negligible, but they must be taken into account when considering spacecraft navigation. The Pioneer anomaly, where the motion of the craft slightly deviated from that expected from gravity alone, was eventually tracked down to asymmetric thermal radiation from the spacecraft. Similarly, the orbits of asteroids are perturbed since the asteroid absorbs solar radiation on the side facing the Sun, but then re-emits the energy at a different angle as the rotation of the asteroid carries the warm surface out of the Sun's view (the YORP effect).
Nanostructures[edit]
Nanostructures with spectrally selective thermal emittance properties offer numerous technological applications for energy generation and efficiency,[24] e.g., for daytime radiative cooling of photovoltaic cells and buildings. These applications require high emittance in the frequency range corresponding to the atmospheric transparency window in 8 to 13 micron wavelength range. A selective emitter radiating strongly in this range is thus exposed to the clear sky, enabling the use of the outer space as a very low temperature heat sink.[25]
Health and safety[edit]
Metabolic temperature regulation[edit]
In a practical, room-temperature setting, humans lose considerable energy due to infrared thermal radiation in addition to that lost by conduction to air (aided by concurrent convection, or other air movement like drafts). The heat energy lost is partially regained by absorbing heat radiation from walls or other surroundings. Human skin has an emissivity of very close to 1.0.[26] A human, having roughly 2 m2 in surface area, and a temperature of about 307 K, continuously radiates approximately 1000 W. If people are indoors, surrounded by surfaces at 296 K, they receive back about 900 W from the wall, ceiling, and other surroundings, resulting in a net loss of 100 W. These estimates are highly dependent on extrinsic variables, such as wearing clothes.
Lighter colors and also whites and metallic substances absorb less of the illuminating light, and as a result heat up less. However, color makes little difference in the heat transfer between an object at everyday temperatures and its surroundings. This is because the dominant emitted wavelengths are not in the visible spectrum, but rather infrared. Emissivities at those wavelengths are largely unrelated to visual emissivities (visible colors); in the far infra-red, most objects have high emissivities. Thus, except in sunlight, the color of clothing makes little difference as regards warmth; likewise, paint color of houses makes little difference to warmth except when the painted part is sunlit.
Burns[edit]
Thermal radiation is a phenomenon that can burn skin and ignite flammable materials. The time to a damage from exposure to thermal radiation is a function of the rate of delivery of the heat. Radiative heat flux and effects are given as follows:[27]
| kW/m2 | Effect |
|---|---|
| 170 | Maximum flux measured in a post-flashover compartment |
| 80 | Thermal Protective Performance test for personal protective equipment |
| 52 | Fiberboard ignites at five seconds |
| 29 | Wood ignites, given time |
| 20 | Typical beginning of flashover at floor level of a residential room |
| 16 | Human skin: sudden pain and second-degree burn blisters after 5 seconds |
| 12.5 | Wood produces ignitable volatiles by pyrolysis |
| 10.4 | Human skin: Pain after 3 seconds, second-degree burn blisters after 9 seconds |
| 6.4 | Human skin: second-degree burn blisters after 18 seconds |
| 4.5 | Human skin: second-degree burn blisters after 30 seconds |
| 2.5 | Human skin: burns after prolonged exposure, radiant flux exposure typically encountered during firefighting |
| 1.4 | Sunlight, sunburns potentially within 30 minutes. Sunburn is NOT a thermal burn. It is caused by cellular damage due to ultraviolet radiation. |
Near-field radiative heat transfer[edit]
At distances on the scale of the wavelength of a radiated electromangetic wave or smaller, Planck's law is not accurate. For objects this small and close together, the quantum tunneling of EM waves has a significant impact on the rate of radiation.[1]
A more sophisticated framework involving electromagnetic theory must be used for smaller distances from the thermal source or surface. For example, although far-field thermal radiation at distances from surfaces of more than one wavelength is generally not coherent to any extent, near-field thermal radiation (i.e., radiation at distances of a fraction of various radiation wavelengths) may exhibit a degree of both temporal and spatial coherence.[28]
Planck's law of thermal radiation has been challenged in recent decades by predictions and successful demonstrations of the radiative heat transfer between objects separated by nanoscale gaps that deviate significantly from the law predictions. This deviation is especially strong (up to several orders in magnitude) when the emitter and absorber support surface polariton modes that can couple through the gap separating cold and hot objects. However, to take advantage of the surface-polariton-mediated near-field radiative heat transfer, the two objects need to be separated by ultra-narrow gaps on the order of microns or even nanometers. This limitation significantly complicates practical device designs.
Another way to modify the object thermal emission spectrum is by reducing the dimensionality of the emitter itself.[24] This approach builds upon the concept of confining electrons in quantum wells, wires and dots, and tailors thermal emission by engineering confined photon states in two- and three-dimensional potential traps, including wells, wires, and dots. Such spatial confinement concentrates photon states and enhances thermal emission at select frequencies.[29] To achieve the required level of photon confinement, the dimensions of the radiating objects should be on the order of or below the thermal wavelength predicted by Planck's law. Most importantly, the emission spectrum of thermal wells, wires and dots deviates from Planck's law predictions not only in the near field, but also in the far field, which significantly expands the range of their applications.
See also[edit]
- Incandescence
- Infrared photography
- Interior radiation control coating
- Heat transfer
- Planck radiation
- Radiant cooling
- Sakuma–Hattori equation
- Thermal dose unit
- View factor
References[edit]
- ^ a b c d Howell, John R.; Mengüç, M. Pinar; Siegel, Robert (2016). Thermal radiation heat transfer (Sixth ed.). Boca Raton, Fla. London New York: CRC Press, Taylor & Francis Group. ISBN 978-1-4665-9326-8.
- ^ a b Meseguer, José. (2012). Spacecraft thermal control. Isabel Pérez-Grande, Angel Sanz-Andrés. Cambridge: Woodhead Pub. ISBN 978-0-85709-608-1. OCLC 903167592.
- ^ a b c d e Planck, M., The Theory of Heat Radiation, P Blakiston's Son & Co., New York, 1914.
- ^ a b Huang, Kerson (1987). Statistical mechanics (2nd ed.). New York: Wiley. ISBN 978-0-471-81518-1.
- ^ a b S. Blundell, K. Blundell (2006). Concepts in Thermal Physics. Oxford University Press. p. 247. ISBN 978-0-19-856769-1.
- ^ a b c d e f Putley, E.H. (1982). "History of infrared detection—part I. The first detectors of thermal radiation". Infrared Physics. 22 (3): 125–131. Bibcode:1982InfPh..22..125P. doi:10.1016/0020-0891(82)90030-6.
- ^ Cohen, I. B. (1943). Franklin’s Experiments on Heat Absorption as a Function of Color. Isis, 34(5), 404–407.
- ^ a b c d Brown, Sanborn C. (1967), "The Caloric Theory", Men of Physics: Benjamin Thompson – Count Rumford, Elsevier, pp. 16–24, doi:10.1016/b978-0-08-012179-6.50008-3, ISBN 9780080121796, retrieved 3 December 2021
- ^ Gillispie, Charles Coulston (1960). The Edge of Objectivity: An Essay in the History of Scientific Ideas. Princeton University Press. pp. 408–9. ISBN 0-691-02350-6.
- ^ Lemons, Don S.; Shanahan, William R.; Buchholtz, Louis J. (20 September 2022). On the Trail of Blackbody Radiation: Max Planck and the Physics of his Era. MIT Press. ISBN 978-0-262-04704-3.
- ^ a b "Pierre Prévost". Oxford Reference. Retrieved 29 February 2024.
- ^ Herschel, William (1800). "Experiments on the refrangibility of the invisible rays of the Sun". Philosophical Transactions of the Royal Society of London. 90: 284–292. doi:10.1098/rstl.1800.0015. JSTOR 107057.
- ^ "Herschel Discovers Infrared Light". Coolcosmos.ipac.caltech.edu. Archived from the original on 25 February 2012. Retrieved 8 November 2011.
- ^ a b c d e Hsu, Shao Ti. Engineering Heat Transfer. Blacksburg, Virginia:D. Van Nostrand Company, Inc.,1962.
- ^ a b Becker, Martin. Heat Transfer a Modern Approach New York: Plenum Publishing Corporation, 1986.
- ^ a b Kirchhoff, G. (July 1860). "I. On the relation between the radiating and absorbing powers of different bodies for light and heat". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 20 (130): 1–21. doi:10.1080/14786446008642901. ISSN 1941-5982.
- ^ Boltzmann, Ludwig (1884). "Ableitung des Stefan'schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie" [Derivation of Stefan's law, concerning the dependency of heat radiation on temperature, from the electromagnetic theory of light]. Annalen der Physik und Chemie (in German). 258 (6): 291–294. Bibcode:1884AnP...258..291B. doi:10.1002/andp.18842580616.
- ^ a b c d Çengel, Yunus A.; Ghajar, Afshin J. (2011). Heat and mass transfer: fundamentals & applications (4th ed.). New York: McGraw-Hill. ISBN 978-0-07-339812-9. OCLC 463634284.
- ^ a b c d e f g h i j k Incropera, Frank P.; DeWitt, David P.; Bergman, Theodore L.; Lavine, Adrienne S., eds. (2013). Principles of heat and mass transfer (7. ed., international student version ed.). Hoboken, NJ: Wiley. ISBN 978-0-470-50197-9.
- ^ "The Physics of Coloured Fireworks". 21 July 2011. Archived from the original on 21 July 2011.
- ^ S. Tanemura, M. Tazawa, P. Jing, T. Miki, K. Yoshimura, K. Igarashi, M. Ohishi, K. Shimono, M. Adachi. "Optical Properties and Radiative Cooling Power of White Paints" (PDF). Archived from the original (PDF) on 2 January 2007. Retrieved 24 January 2010. ISES 1999 Solar World Congress
- ^ Shao, Gaofeng; et al. (2019). "Improved oxidation resistance of high emissivity coatings on fibrous ceramic for reusable space systems". Corrosion Science. 146: 233–246. arXiv:1902.03943. Bibcode:2019Corro.146..233S. doi:10.1016/j.corsci.2018.11.006. S2CID 118927116.
- ^ The Efficient Windows Collaborative: Window Technologies Archived 26 April 2011 at the Wayback Machine
- ^ a b Fan, Shanhui; Li, Wei (11 June 2018). "Nanophotonic control of thermal radiation for energy applications [Invited]". Optics Express. 26 (12): 15995–16021. Bibcode:2018OExpr..2615995L. doi:10.1364/OE.26.015995. ISSN 1094-4087. PMID 30114851.
- ^ Zhai, Yao; Ma, Yaoguang; David, Sabrina N.; Zhao, Dongliang; Lou, Runnan; Tan, Gang; Yang, Ronggui; Yin, Xiaobo (10 March 2017). "Scalable-manufactured randomized glass-polymer hybrid metamaterial for daytime radiative cooling". Science. 355 (6329): 1062–1066. Bibcode:2017Sci...355.1062Z. doi:10.1126/science.aai7899. ISSN 0036-8075. PMID 28183998.
- ^ R. Bowling Barnes (24 May 1963). "Thermography of the Human Body Infrared-radiant energy provides new concepts and instrumentation for medical diagnosis". Science. 140 (3569): 870–877. Bibcode:1963Sci...140..870B. doi:10.1126/science.140.3569.870. PMID 13969373. S2CID 30004363.
- ^ John J. Lentini - Scientific Protocols for Fire Investigation, CRC 2006, ISBN 0849320828, table from NFPA 921, Guide for Fire and Explosion Investigations
- ^ Greffet, Jean-Jacques; Henkel, Carsten (2007). "Coherent thermal radiation". Contemporary Physics. 48 (4): 183–194. Bibcode:2007ConPh..48..183G. doi:10.1080/00107510701690380. S2CID 121228286.
- ^ Rephaeli, Eden; Raman, Aaswath; Fan, Shanhui (2013). "Ultrabroadband photonic structures to achieve high-performance daytime radiative cooling". Nano Letters. 13 (4): 1457–1461. Bibcode:2013NanoL..13.1457R. doi:10.1021/nl4004283. PMID 23461597. S2CID 27762117.
Further reading[edit]
- Siegel, John R. Howell, Robert; Howell. John R. (November 2001). Thermal radiation heat transfer. New York: Taylor & Francis, Inc. pp. (xix – xxvi list of symbols for thermal radiation formulas). ISBN 978-1-56032-839-1. Retrieved 23 July 2009.
- E.M. Sparrow and R.D. Cess. Radiation Heat Transfer. Hemisphere Publishing Corporation, 1978.
- Kuenzer, C. and S. Dech (2013): Thermal Infrared Remote Sensing: Sensors, Methods, Applications (= Remote Sensing and Digital Image Processing 17). Dordrecht: Springer.


















































