Rectified 24-cell

Rectified 24-cell
Schlegel diagram 8 of 24 cuboctahedral cells shown
Type	Uniform polychoron
Schläfli symbol	t1{3,4,3} t0,2{3,3,4} t0,2,3{31,1,1}
Coxeter-Dynkin diagrams
Cells	48	24 3.4.3.4 24 4.4.4
Faces	240	96 {3} 144 {4}
Edges	288
Vertices	96
Vertex figure	Triangular prism
Symmetry groups	F4 [3,4,3] B4 [3,3,4] D4 [31,1,1]
Properties	convex, edge-transitive
Uniform index	22 23 24

In geometry, the rectified 24-cell is a uniform 4-dimensional polytope (or uniform polychoron), which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.

It can also be considered a cantellated 16-cell with the lower symmetries B₄ = [3,3,4]. B₄ would lead to a bicoloring of the cuboctahedral cells into 8 and 16 each. It is also called a runcicantellated demitesseract in a D₄ symmetry, giving 3 colors of cells, 8 for each.

Cartesian coordinates

A rectified 24-cell having an edge length of √2 has vertices given by all permutations and sign permutations of the following Cartesian coordinates:

(0,1,1,2) [4!/2!x2³ = 96 vertices]

The dual configuration has all coordinate and sign permutations of:

(0,2,2,2) [4x2³ = 32 vertices]

(1,1,1,3) [4x2⁴ = 64 vertices]

Images

orthographic projections

Coxeter plane	F4
Graph
Dihedral symmetry	[12]
Coxeter plane	B3 / A2 (a)	B3 / A2 (b)
Graph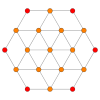
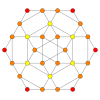
Dihedral symmetry	[6]	[6]
Coxeter plane	B4	B2 / A2
Graph
Dihedral symmetry	[8]	[4]

Stereographic projection
Center of stereographic projection with 96 triangular faces blue

Symmetry constructions

There are three different symmetry constructions of this polytope. The lowest D₃ construction can be doubled into C₃ by adding a mirror that maps the bifurcating nodes onto each other. D₃ can be mapped up to F₃ symmetry by adding two mirror that map all three end nodes together.

The vertex figure is a triangular prism, containing two cubes and three cuboctahedra. The three symmetries can be seen with 3 colored cuboctahedra in the lowest D₃ construction, and two colors (1:2 ratio) in C₃, and all identical cuboctahedra in F₃.

In F₃ symmetry one further symmetry exists that maps the two cubes in the vertex figure onto each other, represented by Coxeter symmetry notation [[3,4,3]], and having a doubled order of 2304.

Coxeter group	Order	Full symmetry group	Coxeter-Dynkin diagram	Facets	Vertex figure
F3 = [3,4,3]	1152 (2304)	[[3,4,3]]		3: 2:
C3 = [4,3,3]	384	[4,3,3]		2,2: 2:
D3 = [3,31,1]	192	<[3,31,1]> = [4,3,3] [3[31,1,1]] = [3,4,3]		1,1,1: 2:

Alternate names

• Rectified 24-cell (Norman Johnson)
  • Cantellated 16-cell (Norman Johnson)
• Rectified icositetrachoron (Acronym rico) (George Olshevsky, Jonathan Bowers)
  • Cantellated hexadecachoron
• Rectified polyoctahedron
• Disicositetrachoron
• Amboicositetrachoron (Neil Sloane & John Horton Conway)

Related uniform polytopes

Name	24-cell	truncated 24-cell	rectified 24-cell	cantellated 24-cell	bitruncated 24-cell	cantitruncated 24-cell	runcinated 24-cell	runcitruncated 24-cell	omnitruncated 24-cell	snub 24-cell
Schläfli symbol	{3,4,3}	t0,1{3,4,3}	t1{3,4,3}	t0,2{3,4,3}	t1,2{3,4,3}	t0,1,2{3,4,3}	t0,3{3,4,3}	t0,1,3{3,4,3}	t0,1,2,3{3,4,3}	h0,1{3,4,3}
Coxeter-Dynkin diagram
Schlegel diagram
F4
B4
B3(a)
B3(b)
B2

The rectified 24-cell can also be derived as a cantellated 16-cell:

Name	tesseract	rectified tesseract	truncated tesseract	cantellated tesseract	runcinated tesseract	bitruncated tesseract	cantitruncated tesseract	runcitruncated tesseract	omnitruncated tesseract
Coxeter-Dynkin diagram
Schläfli symbol	{4,3,3}	t1{4,3,3}	t0,1{4,3,3}	t0,2{4,3,3}	t0,3{4,3,3}	t1,2{4,3,3}	t0,1,2{4,3,3}	t0,1,3{4,3,3}	t0,1,2,3{4,3,3}
Schlegel diagram
B4 Coxeter plane graph
Name	16-cell	rectified 16-cell	truncated 16-cell	cantellated 16-cell	runcinated 16-cell	bitruncated 16-cell	cantitruncated 16-cell	runcitruncated 16-cell	omnitruncated 16-cell
Coxeter-Dynkin diagram
Schläfli symbol	{3,3,4}	t1{3,3,4}	t0,1{3,3,4}	t0,2{3,3,4}	t0,3{3,3,4}	t1,2{3,3,4}	t0,1,2{3,3,4}	t0,1,3{3,3,4}	t0,1,2,3{3,3,4}
Schlegel diagram
B4 Coxeter plane graph

References

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• H.S.M. Coxeter:
  • Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
• 2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Model 23, George Olshevsky.
  • 3. Convex uniform polychora based on the icositetrachoron (24-cell) - Model 23, George Olshevsky.
  • 7. Uniform polychora derived from glomeric tetrahedron B4 - Model 23, George Olshevsky.
• Richard Klitzing, 4D uniform polytopes (polychora), o3x4o3o - rico