Optical fiber

A bundle of optical fibers

A TOSLINK fiber optic audio cable being illuminated at one end

An optical fiber is a thin, flexible, transparent fiber that acts as a waveguide, or "light pipe", to transmit light between the two ends of the fiber. The field of applied science and engineering concerned with the design and application of optical fibers is known as fiber optics. Optical fibers are widely used in fiber-optic communications, which permits transmission over longer distances and at higher bandwidths (data rates) than other forms of communication. Fibers are used instead of metal wires because signals travel along them with less loss and are also immune to electromagnetic interference. Fibers are also used for illumination, and are wrapped in bundles so they can be used to carry images, thus allowing viewing in tight spaces. Specially designed fibers are used for a variety of other applications, including sensors and fiber lasers.

Optical fiber typically consists of a transparent core surrounded by a transparent cladding material with a lower index of refraction. Light is kept in the core by total internal reflection. This causes the fiber to act as a waveguide. Fibers that support many propagation paths or transverse modes are called multi-mode fibers (MMF), while those that only support a single mode are called single-mode fibers (SMF). Multi-mode fibers generally have a larger core diameter, and are used for short-distance communication links and for applications where high power must be transmitted. Single-mode fibers are used for most communication links longer than 1,050 meters (3,440 ft).

Joining lengths of optical fiber is more complex than joining electrical wire or cable. The ends of the fibers must be carefully cleaved, and then spliced together either mechanically or by fusing them together with heat. Special optical fiber connectors removable connections.

History

Daniel Colladon first described this "light fountain" or "light pipe" in an 1842 article titled On the reflections of a ray of light inside a parabolic liquid stream. This particular illustration comes from a later article by Colladon, in 1884.

Fiber optics, though used extensively in the modern world, is a fairly simple and old technology. Guiding of light by refraction, the principle that makes fiber optics possible, was first demonstrated by Daniel Colladon and Jacques Babinet in Paris in the early 1840s. John Tyndall included a demonstration of it in his public lectures in London a dozen years later. Tyndall also wrote about the property of total internal reflection in an introductory book about the nature of light in 1870: "When the light passes from air into water, the refracted ray is bent towards the perpendicular... When the ray passes from water to air it is bent from the perpendicular... If the angle which the ray in water encloses with the perpendicular to the surface be greater than 48 degrees, the ray will not quit the water at all: it will be totally reflected at the surface.... The angle which marks the limit where total reflection begins is called the limiting angle of the medium. For water this angle is 48°27', for flint glass it is 38°41', while for diamond it is 23°42'." Unpigmented human hairs have also been to shown to act as an optical fibre.

Practical applications, such as close internal illumination during dentistry, appeared early in the twentieth century. Image transmission through tubes was demonstrated independently by the radio experimenter Clarence Hansell and the television pioneer John Logie Baird in the 1920s. The principle was first used for internal medical examinations by Heinrich Lamm in the following decade. In 1952, physicist Narinder Singh Kapany conducted experiments that led to the invention of optical fiber. Modern optical fibers, where the glass fiber is coated with a transparent cladding to offer a more suitable refractive index, appeared later in the decade. Development then focused on fiber bundles for image transmission. The first fiber optic semi-flexible gastroscope was patented by Basil Hirschowitz, C. Wilbur Peters, and Lawrence E. Curtiss, researchers at the University of Michigan, in 1956. In the process of developing the gastroscope, Curtiss produced the first glass-clad fibers; previous optical fibers had relied on air or impractical oils and waxes as the low-index cladding material. A variety of other image transmission applications soon followed.

In the late 19th and early 20th centuries, light was guided through bent glass rods to illuminate body cavities. Alexander Graham Bell invented a 'Photophone' to transmit voice signals over an optical beam.

Jun-ichi Nishizawa, a Japanese scientist at Tohoku University, also proposed the use of optical fibers for communications in 1963, as stated in his book published in 2004 in India. Nishizawa invented other technologies that contributed to the development of optical fiber communications, such as the graded-index optical fiber as a channel for transmitting light from semiconductor lasers. Charles K. Kao and George A. Hockham of the British company Standard Telephones and Cables (STC) were the first to promote the idea that the attenuation in optical fibers could be reduced below 20 decibels per kilometer (dB/km), making fibers a practical communication medium. They proposed that the attenuation in fibers available at the time was caused by impurities that could be removed, rather than by fundamental physical effects such as scattering. They correctly and systematically theorized the light-loss properties for optical fiber, and pointed out the right material to use for such fibers — silica glass with high purity. This discovery earned Kao the Nobel Prize in Physics in 2009.

NASA used fiber optics in the television cameras sent to the moon. At the time, the use in the cameras was classified confidential, and only those with the right security clearance or those accompanied by someone with the right security clearance were permitted to handle the cameras.

The crucial attenuation limit of 20 dB/km was first achieved in 1970, by researchers Robert D. Maurer, Donald Keck, Peter C. Schultz, and Frank Zimar working for American glass maker Corning Glass Works, now Corning Incorporated. They demonstrated a fiber with 17 dB/km attenuation by doping silica glass with titanium. A few years later they produced a fiber with only 4 dB/km attenuation using germanium dioxide as the core dopant. Such low attenuation ushered in optical fiber telecommunication. In 1981, General Electric produced fused quartz ingots that could be drawn into fiber optic strands 25 miles (40 km) long.

Attenuation in modern optical cables is far less than in electrical copper cables, leading to long-haul fiber connections with repeater distances of 70–150 kilometers (43–93 mi). The erbium-doped fiber amplifier, which reduced the cost of long-distance fiber systems by reducing or eliminating optical-electrical-optical repeaters, was co-developed by teams led by David N. Payne of the University of Southampton and Emmanuel Desurvire at Bell Labs in 1986. Robust modern optical fiber uses glass for both core and sheath, and is therefore less prone to aging. It was invented by Gerhard Bernsee of Schott Glass in Germany in 1973.

The emerging field of photonic crystals led to the development in 1991 of photonic-crystal fiber, which guides light by diffraction from a periodic structure, rather than by total internal reflection. The first photonic crystal fibers became commercially available in 2000. Photonic crystal fibers can carry higher power than conventional fibers and their wavelength-dependent properties can be manipulated to improve performance.

Applications

Optical fiber communication

Main article: Fiber-optic communication

Optical fiber can be used as a medium for telecommunication and networking because it is flexible and can be bundled as cables. It is especially advantageous for long-distance communications, because light propagates through the fiber with little attenuation compared to electrical cables. This allows long distances to be spanned with few repeaters. Additionally, the per-channel light signals propagating in the fiber have been modulated at rates as high as 111 gigabits per second by NTT, although 10 or 40 Gbit/s is typical in deployed systems. Each fiber can carry many independent channels, each using a different wavelength of light (wavelength-division multiplexing (WDM)). The net data rate (data rate without overhead bytes) per fiber is the per-channel data rate reduced by the FEC overhead, multiplied by the number of channels (usually up to eighty in commercial dense WDM systems as of 2008). The current laboratory fiber optic data rate record, held by Bell Labs in Villarceaux, France, is multiplexing 155 channels, each carrying 100 Gbit/s over a 7000 km fiber. Nippon Telegraph and Telephone Corporation have also managed 69.1 Tbit/s over a single 240 km fiber (multiplexing 432 channels, equating to 171 Gbit/s per channel). Bell Labs also broke a 100 Petabit per second kilometer barrier (15.5 Tbit/s over a single 7000 km fiber).

For short distance applications, such as a network in an office building, fiber-optic cabling can save space in cable ducts. This is because a single fiber can carry much more data than electrical cables such as 4 pair Cat-5 Ethernet cabling. Fiber is also immune to electrical interference; there is no cross-talk between signals in different cables, and no pickup of environmental noise. Non-armored fiber cables do not conduct electricity, which makes fiber a good solution for protecting communications equipment in high voltage environments, such as power generation facilities, or metal communication structures prone to lightning strikes. They can also be used in environments where explosive fumes are present, without danger of ignition. Wiretapping is more difficult compared to electrical connections, and there are concentric dual core fibers that are said to be tap-proof.

Fiber optic sensors

Main article: Fiber optic sensor

Fibers have many uses in remote sensing. In some applications, the sensor is itself an optical fiber. In other cases, fiber is used to connect a non-fiberoptic sensor to a measurement system. Depending on the application, fiber may be used because of its small size, or the fact that no electrical power is needed at the remote location, or because many sensors can be multiplexed along the length of a fiber by using different wavelengths of light for each sensor, or by sensing the time delay as light passes along the fiber through each sensor. Time delay can be determined using a device such as an optical time-domain reflectometer.

Optical fibers can be used as sensors to measure strain, temperature, pressure and other quantities by modifying a fiber so that the property to measure modulates the intensity, phase, polarization, wavelength, or transit time of light in the fiber. Sensors that vary the intensity of light are the simplest, since only a simple source and detector are required. A particularly useful feature of such fiber optic sensors is that they can, if required, provide distributed sensing over distances of up to one meter.

Extrinsic fiber optic sensors use an optical fiber cable, normally a multi-mode one, to transmit modulated light from either a non-fiber optical sensor—or an electronic sensor connected to an optical transmitter. A major benefit of extrinsic sensors is their ability to reach otherwise inaccessible places. An example is the measurement of temperature inside aircraft jet engines by using a fiber to transmit radiation into a radiation pyrometer outside the engine. Extrinsic sensors can be used in the same way to measure the internal temperature of electrical transformers, where the extreme electromagnetic fields present make other measurement techniques impossible. Extrinsic sensors measure vibration, rotation, displacement, velocity, acceleration, torque, and twisting. A solid state version of the gyroscope, using the interference of light, has been developed. The fiber optic gyroscope (FOG) has no moving parts, and exploits the Sagnac effect to detect mechanical rotation.

Common uses for fiber optic sensors includes advanced intrusion detection security systems. The light is transmitted along a fiber optic sensor cable placed on a fence, pipeline, or communication cabling, and the returned signal is monitored and analysed for disturbances. This return signal is digitally processed to detect disturbances and trip an alarm if an intrusion has occurred.

Other uses of optical fibers

A frisbee illuminated by fiber optics

Light reflected from optical fiber illuminates exhibited model

Fiber optic front sight on a hand gun

Fibers are widely used in illumination applications. They are used as light guides in medical and other applications where bright light needs to be shone on a target without a clear line-of-sight path. In some buildings, optical fibers route sunlight from the roof to other parts of the building (see non-imaging optics). Optical fiber illumination is also used for decorative applications, including signs, art, and artificial Christmas trees. Swarovski boutiques use optical fibers to illuminate their crystal showcases from many different angles while only employing one light source. Optical fiber is an intrinsic part of the light-transmitting concrete building product, LiTraCon.

Optical fiber is also used in imaging optics. A coherent bundle of fibers is used, sometimes along with lenses, for a long, thin imaging device called an endoscope, which is used to view objects through a small hole. Medical endoscopes are used for minimally invasive exploratory or surgical procedures (endoscopy). Industrial endoscopes (see fiberscope or borescope) are used for inspecting anything hard to reach, such as jet engine interiors.

In spectroscopy, optical fiber bundles transmit light from a spectrometer to a substance that cannot be placed inside the spectrometer itself, in order to analyze its composition. A spectrometer analyzes substances by bouncing light off of and through them. By using fibers, a spectrometer can be used to study objects that are too large to fit inside, or gasses, or reactions in pressure vessels.

An optical fiber doped with certain rare earth elements such as erbium can be used as the gain medium of a laser or optical amplifier. Rare-earth doped optical fibers can be used to provide signal amplification by splicing a short section of doped fiber into a regular (undoped) optical fiber line. The doped fiber is optically pumped with a second laser wavelength that is coupled into the line in addition to the signal wave. Both wavelengths of light are transmitted through the doped fiber, which transfers energy from the second pump wavelength to the signal wave. The process that causes the amplification is stimulated emission.

Optical fibers doped with a wavelength shifter collect scintillation light in physics experiments.

Optical fiber can be used to supply a low level of power (around one watt) to electronics situated in a difficult electrical environment. Examples of this are electronics in high-powered antenna elements and measurement devices used in high voltage transmission equipment.

A growing trend in iron sights for arms, is the use of short pieces of optical fiber for contrast enhancement dots, made in such a way that ambient light falling on the length of the fiber is concentrated at the tip, making the dots slightly brighter than the surroundings. This method is most commonly used in front sights, but many makers offer sights that use fiber optics on front and rear sights. Fiber optic sights can now be found on handguns, rifles, and shotguns, both as aftermarket accessories and a growing number of factory guns.

Principle of operation

An optical fiber is a cylindrical dielectric waveguide (nonconducting waveguide) that transmits light along its axis, by the process of total internal reflection. The fiber consists of a core surrounded by a cladding layer, both of which are made of dielectric materials. To confine the optical signal in the core, the refractive index of the core must be greater than that of the cladding. The boundary between the core and cladding may either be abrupt, in step-index fiber, or gradual, in graded-index fiber.

Index of refraction

Main article: Refractive index

The index of refraction is a way of measuring the speed of light in a material. Light travels fastest in a vacuum, such as outer space. The speed of light in a vacuum is about 300,000 kilometres (186 thousand miles) per second. Index of refraction is calculated by dividing the speed of light in a vacuum by the speed of light in some other medium. The index of refraction of a vacuum is therefore 1, by definition. The typical value for the cladding of an optical fiber is 1.52. The core value is typically 1.62. The larger the index of refraction, the slower light travels in that medium. From this information, a good rule of thumb is that signal using optical fiber for communication will travel at around 200 million meters per second. Or to put it another way, to travel 1000 kilometers in fiber, the signal will take 5 milliseconds to propagate. Thus a phone call carried by fiber between Sydney and New York, a 12000 kilometer distance, means that there is an absolute minimum delay of 60 milliseconds (or around 1/16 of a second) between when one caller speaks to when the other hears. (Of course the fiber in this case will probably travel a longer route, and there will be additional delays due to communication equipment switching and the process of encoding and decoding the voice onto the fiber).

Total internal reflection

Main article: Total internal reflection

When light traveling in a dense medium hits a boundary at a steep angle (larger than the "critical angle" for the boundary), the light will be completely reflected. This effect is used in optical fibers to confine light in the core. Light travels along the fiber bouncing back and forth off of the boundary. Because the light must strike the boundary with an angle greater than the critical angle, only light that enters the fiber within a certain range of angles can travel down the fiber without leaking out. This range of angles is called the acceptance cone of the fiber. The size of this acceptance cone is a function of the refractive index difference between the fiber's core and cladding.

In simpler terms, there is a maximum angle from the fiber axis at which light may enter the fiber so that it will propagate, or travel, in the core of the fiber. The sine of this maximum angle is the numerical aperture (NA) of the fiber. Fiber with a larger NA requires less precision to splice and work with than fiber with a smaller NA. Single-mode fiber has a small NA.

Multi-mode fiber

The propagation of light through a multi-mode optical fiber.

A laser bouncing down an acrylic rod, illustrating the total internal reflection of light in a multi-mode optical fiber.

Main article: Multi-mode optical fiber

Fiber with large core diameter (greater than 10 micrometers) may be analyzed by geometrical optics. Such fiber is called multi-mode fiber, from the electromagnetic analysis (see below). In a step-index multi-mode fiber, rays of light are guided along the fiber core by total internal reflection. Rays that meet the core-cladding boundary at a high angle (measured relative to a line normal to the boundary), greater than the critical angle for this boundary, are completely reflected. The critical angle (minimum angle for total internal reflection) is determined by the difference in index of refraction between the core and cladding materials. Rays that meet the boundary at a low angle are refracted from the core into the cladding, and do not convey light and hence information along the fiber. The critical angle determines the acceptance angle of the fiber, often reported as a numerical aperture. A high numerical aperture allows light to propagate down the fiber in rays both close to the axis and at various angles, allowing efficient coupling of light into the fiber. However, this high numerical aperture increases the amount of dispersion as rays at different angles have different path lengths and therefore take different times to traverse the fiber.

Optical fiber types.

In graded-index fiber, the index of refraction in the core decreases continuously between the axis and the cladding. This causes light rays to bend smoothly as they approach the cladding, rather than reflecting abruptly from the core-cladding boundary. The resulting curved paths reduce multi-path dispersion because high angle rays pass more through the lower-index periphery of the core, rather than the high-index center. The index profile is chosen to minimize the difference in axial propagation speeds of the various rays in the fiber. This ideal index profile is very close to a parabolic relationship between the index and the distance from the axis.

Single-mode fiber

The structure of a typical single-mode fiber.
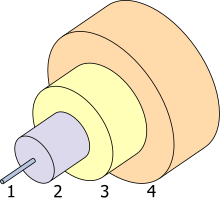
1. Core: 8 µm diameter
2. Cladding: 125 µm dia.
3. Buffer: 250 µm dia.
4. Jacket: 400 µm dia.

Main article: Single-mode optical fiber

Fiber with a core diameter less than about ten times the wavelength of the propagating light cannot be modeled using geometric optics. Instead, it must be analyzed as an electromagnetic structure, by solution of Maxwell's equations as reduced to the electromagnetic wave equation. The electromagnetic analysis may also be required to understand behaviors such as speckle that occur when coherent light propagates in multi-mode fiber. As an optical waveguide, the fiber supports one or more confined transverse modes by which light can propagate along the fiber. Fiber supporting only one mode is called single-mode or mono-mode fiber. The behavior of larger-core multi-mode fiber can also be modeled using the wave equation, which shows that such fiber supports more than one mode of propagation (hence the name). The results of such modeling of multi-mode fiber approximately agree with the predictions of geometric optics, if the fiber core is large enough to support more than a few modes.

The waveguide analysis shows that the light energy in the fiber is not completely confined in the core. Instead, especially in single-mode fibers, a significant fraction of the energy in the bound mode travels in the cladding as an evanescent wave.

The most common type of single-mode fiber has a core diameter of 8–10 micrometers and is designed for use in the near infrared. The mode structure depends on the wavelength of the light used, so that this fiber actually supports a small number of additional modes at visible wavelengths. Multi-mode fiber, by comparison, is manufactured with core diameters as small as 50 micrometers and as large as hundreds of micrometers. The normalized frequency V for this fiber should be less than the first zero of the Bessel function J₀ (approximately 2.405).

Special-purpose fiber

Some special-purpose optical fiber is constructed with a non-cylindrical core and/or cladding layer, usually with an elliptical or rectangular cross-section. These include polarization-maintaining fiber and fiber designed to suppress whispering gallery mode propagation.

Photonic-crystal fiber is made with a regular pattern of index variation (often in the form of cylindrical holes that run along the length of the fiber). Such fiber uses diffraction effects instead of or in addition to total internal reflection, to confine light to the fiber's core. The properties of the fiber can be tailored to a wide variety of applications.

Mechanisms of attenuation

Light attenuation by ZBLAN and silica fibers

Main article: Transparent materials

Attenuation in fiber optics, also known as transmission loss, is the reduction in intensity of the light beam (or signal) with respect to distance traveled through a transmission medium. Attenuation coefficients in fiber optics usually use units of dB/km through the medium due to the relatively high quality of transparency of modern optical transmission media. The medium is usually a fiber of silica glass that confines the incident light beam to the inside. Attenuation is an important factor limiting the transmission of a digital signal across large distances. Thus, much research has gone into both limiting the attenuation and maximizing the amplification of the optical signal. Empirical research has shown that attenuation in optical fiber is caused primarily by both scattering and absorption.

Light scattering

Specular reflection

Diffuse reflection

The propagation of light through the core of an optical fiber is based on total internal reflection of the lightwave. Rough and irregular surfaces, even at the molecular level, can cause light rays to be reflected in random directions. This is called diffuse reflection or scattering, and it is typically characterized by wide variety of reflection angles.

Light scattering depends on the wavelength of the light being scattered. Thus, limits to spatial scales of visibility arise, depending on the frequency of the incident light-wave and the physical dimension (or spatial scale) of the scattering center, which is typically in the form of some specific micro-structural feature. Since visible light has a wavelength of the order of one micrometre (one millionth of a meter) scattering centers will have dimensions on a similar spatial scale.

Thus, attenuation results from the incoherent scattering of light at internal surfaces and interfaces. In (poly)crystalline materials such as metals and ceramics, in addition to pores, most of the internal surfaces or interfaces are in the form of grain boundaries that separate tiny regions of crystalline order. It has recently been shown that when the size of the scattering center (or grain boundary) is reduced below the size of the wavelength of the light being scattered, the scattering no longer occurs to any significant extent. This phenomenon has given rise to the production of transparent ceramic materials.

Similarly, the scattering of light in optical quality glass fiber is caused by molecular level irregularities (compositional fluctuations) in the glass structure. Indeed, one emerging school of thought is that a glass is simply the limiting case of a polycrystalline solid. Within this framework, "domains" exhibiting various degrees of short-range order become the building blocks of both metals and alloys, as well as glasses and ceramics. Distributed both between and within these domains are micro-structural defects that provide the most ideal locations for light scattering. This same phenomenon is seen as one of the limiting factors in the transparency of IR missile domes.

At high optical powers, scattering can also be caused by nonlinear optical processes in the fiber.

UV-Vis-IR absorption

In addition to light scattering, attenuation or signal loss can also occur due to selective absorption of specific wavelengths, in a manner similar to that responsible for the appearance of color. Primary material considerations include both electrons and molecules as follows:

1) At the electronic level, it depends on whether the electron orbitals are spaced (or "quantized") such that they can absorb a quantum of light (or photon) of a specific wavelength or frequency in the ultraviolet (UV) or visible ranges. This is what gives rise to color.

2) At the atomic or molecular level, it depends on the frequencies of atomic or molecular vibrations or chemical bonds, how close-packed its atoms or molecules are, and whether or not the atoms or molecules exhibit long-range order. These factors will determine the capacity of the material transmitting longer wavelengths in the infrared (IR), far IR, radio and microwave ranges.

The design of any optically transparent device requires the selection of materials based upon knowledge of its properties and limitations. The lattice  absorption characteristics observed at the lower frequency regions (mid IR to far-infrared wavelength range) define the long-wavelength transparency limit of the material. They are the result of the interactive coupling between the motions of thermally induced vibrations of the constituent atoms and molecules of the solid lattice and the incident light wave radiation. Hence, all materials are bounded by limiting regions of absorption caused by atomic and molecular vibrations (bond-stretching)in the far-infrared (>10 µm).

Thus, multi-phonon absorption occurs when two or more phonons simultaneously interact to produce electric dipole moments with which the incident radiation may couple. These dipoles can absorb energy from the incident radiation, reaching a maximum coupling with the radiation when the frequency is equal to the fundamental vibrational mode of the molecular dipole (e.g. Si-O bond) in the far-infrared, or one of its harmonics.

The selective absorption of infrared (IR) light by a particular material occurs because the selected frequency of the light wave matches the frequency (or an integer multiple of the frequency) at which the particles of that material vibrate. Since different atoms and molecules have different natural frequencies of vibration, they will selectively absorb different frequencies (or portions of the spectrum) of infrared (IR) light.

Reflection and transmission of light waves occur because the frequencies of the light waves do not match the natural resonant frequencies of vibration of the objects. When IR light of these frequencies strikes an object, the energy is either reflected or transmitted.

Manufacturing

Materials

Glass optical fibers are almost always made from silica, but some other materials, such as fluorozirconate, fluoroaluminate, and chalcogenide glasses as well as crystalline materials like sapphire, are used for longer-wavelength infrared or other specialized applications. Silica and fluoride glasses usually have refractive indices of about 1.5, but some materials such as the chalcogenides can have indices as high as 3. Typically the index difference between core and cladding is less than one percent.

Plastic optical fibers (POF) are commonly step-index multi-mode fibers with a core diameter of 0.5 millimeters or larger. POF typically have higher attenuation coefficients than glass fibers, 1 dB/m or higher, and this high attenuation limits the range of POF-based systems.

Silica

Silica exhibits fairly good optical transmission over a wide range of wavelengths. In the near-infrared (near IR) portion of the spectrum, particularly around 1.5 μm, silica can have extremely low absorption and scattering losses of the order of 0.2 dB/km. A high transparency in the 1.4-μm region is achieved by maintaining a low concentration of hydroxyl groups (OH). Alternatively, a high OH concentration is better for transmission in the ultraviolet (UV) region.

Silica can be drawn into fibers at reasonably high temperatures, and has a fairly broad glass transformation range. One other advantage is that fusion splicing and cleaving of silica fibers is relatively effective. Silica fiber also has high mechanical strength against both pulling and even bending, provided that the fiber is not too thick and that the surfaces have been well prepared during processing. Even simple cleaving (breaking) of the ends of the fiber can provide nicely flat surfaces with acceptable optical quality. Silica is also relatively chemically inert. In particular, it is not hygroscopic (does not absorb water).

Silica glass can be doped with various materials. One purpose of doping is to raise the refractive index (e.g. with Germanium dioxide (GeO₂) or Aluminium oxide (Al₂O₃)) or to lower it (e.g. with fluorine or Boron trioxide (B₂O₃)). Doping is also possible with laser-active ions (for example, rare earth-doped fibers) in order to obtain active fibers to be used, for example, in fiber amplifiers or laser applications. Both the fiber core and cladding are typically doped, so that the entire assembly (core and cladding) is effectively the same compound (e.g. an aluminosilicate, germanosilicate, phosphosilicate or borosilicate glass).

Particularly for active fibers, pure silica is usually not a very suitable host glass, because it exhibits a low solubility for rare earth ions. This can lead to quenching effects due to clustering of dopant ions. Aluminosilicates are much more effective in this respect.

Silica fiber also exhibits a high threshold for optical damage. This property ensures a low tendency for laser-induced breakdown. This is important for fiber amplifiers when utilized for the amplification of short pulses.

Because of these properties silica fibers are the material of choice in many optical applications, such as communications (except for very short distances with plastic optical fiber), fiber lasers, fiber amplifiers, and fiber-optic sensors. Large efforts put forth in the development of various types of silica fibers have further increased the performance of such fibers over other materials.

Fluorides

Fluoride glass is a class of non-oxide optical quality glasses composed of fluorides of various metals. Because of their low viscosity, it is very difficult to completely avoid crystallization while processing it through the glass transition (or drawing the fiber from the melt). Thus, although heavy metal fluoride glasses (HMFG) exhibit very low optical attenuation, they are not only difficult to manufacture, but are quite fragile, and have poor resistance to moisture and other environmental attacks. Their best attribute is that they lack the absorption band associated with the hydroxyl (OH) group (3200–3600 cm⁻¹), which is present in nearly all oxide-based glasses.

An example of a heavy metal fluoride glass is the ZBLAN glass group, composed of zirconium, barium, lanthanum, aluminium, and sodium fluorides. Their main technological application is as optical waveguides in both planar and fiber form. They are advantageous especially in the mid-infrared (2000–5000 nm) range.

HMFGs were initially slated for optical fiber applications, because the intrinsic losses of a mid-IR fiber could in principle be lower than those of silica fibers, which are transparent only up to about 2 μm. However, such low losses were never realized in practice, and the fragility and high cost of fluoride fibers made them less than ideal as primary candidates. Later, the utility of fluoride fibers for various other applications was discovered. These include mid-IR spectroscopy, fiber optic sensors, thermometry, and imaging. Also, fluoride fibers can be used for guided lightwave transmission in media such as YAG (yttria-alumina garnet) lasers at 2.9 μm, as required for medical applications (e.g. ophthalmology and dentistry).

Phosphates

The P₄O₁₀ cagelike structure—the basic building block for phosphate glass.

Phosphate glass constitutes a class of optical glasses composed of metaphosphates of various metals. Instead of the SiO₄ tetrahedra observed in silicate glasses, the building block for this glass former is Phosphorus pentoxide (P₂O₅), which crystallizes in at least four different forms. The most familiar polymorph (see figure) comprises molecules of P₄O₁₀.

Phosphate glasses can be advantageous over silica glasses for optical fibers with a high concentration of doping rare earth ions. A mix of fluoride glass and phosphate glass is fluorophosphate glass.

Chalcogenides

The chalcogens—the elements in group 16 of the periodic table—particularly sulfur (S), selenium (Se) and tellurium (Te)—react with more electropositive elements, such as silver, to form chalcogenides. These are extremely versatile compounds, in that they can be crystalline or amorphous, metallic or semiconducting, and conductors of ions or electrons.

Process

Illustration of the modified chemical vapor deposition (inside) process

Standard optical fibers are made by first constructing a large-diameter "preform", with a carefully controlled refractive index profile, and then "pulling" the preform to form the long, thin optical fiber. The preform is commonly made by three chemical vapor deposition methods: inside vapor deposition, outside vapor deposition, and vapor axial deposition.

With inside vapor deposition, the preform starts as a hollow glass tube approximately 40 centimeters (16 in) long, which is placed horizontally and rotated slowly on a lathe. Gases such as silicon tetrachloride (SiCl₄) or germanium tetrachloride (GeCl₄) are injected with oxygen in the end of the tube. The gases are then heated by means of an external hydrogen burner, bringing the temperature of the gas up to 1900 K (1600 °C, 3000 °F), where the tetrachlorides react with oxygen to produce silica or germania (germanium dioxide) particles. When the reaction conditions are chosen to allow this reaction to occur in the gas phase throughout the tube volume, in contrast to earlier techniques where the reaction occurred only on the glass surface, this technique is called modified chemical vapor deposition (MCVD).

The oxide particles then agglomerate to form large particle chains, which subsequently deposit on the walls of the tube as soot. The deposition is due to the large difference in temperature between the gas core and the wall causing the gas to push the particles outwards (this is known as thermophoresis). The torch is then traversed up and down the length of the tube to deposit the material evenly. After the torch has reached the end of the tube, it is then brought back to the beginning of the tube and the deposited particles are then melted to form a solid layer. This process is repeated until a sufficient amount of material has been deposited. For each layer the composition can be modified by varying the gas composition, resulting in precise control of the finished fiber's optical properties.

In outside vapor deposition or vapor axial deposition, the glass is formed by flame hydrolysis, a reaction in which silicon tetrachloride and germanium tetrachloride are oxidized by reaction with water (H₂O) in an oxyhydrogen flame. In outside vapor deposition the glass is deposited onto a solid rod, which is removed before further processing. In vapor axial deposition, a short seed rod is used, and a porous preform, whose length is not limited by the size of the source rod, is built up on its end. The porous preform is consolidated into a transparent, solid preform by heating to about 1800 K (1500 °C, 2800 °F).

The preform, however constructed, is then placed in a device known as a drawing tower, where the preform tip is heated and the optic fiber is pulled out as a string. By measuring the resultant fiber width, the tension on the fiber can be controlled to maintain the fiber thickness.

Coatings

The light is "guided" down the core of the fiber by an optical "cladding" with a lower refractive index that traps light in the core through "total internal reflection."

The cladding is coated by a "buffer" that protects it from moisture and physical damage. The buffer is what gets stripped off the fiber for termination or splicing. These coatings are UV-cured urethane acrylate composite materials applied to the outside of the fiber during the drawing process. The coatings protect the very delicate strands of glass fiber—about the size of a human hair—and allow it to survive the rigors of manufacturing, proof testing, cabling and installation.

Today’s glass optical fiber draw processes employ a dual-layer coating approach. An inner primary coating is designed to act as a shock absorber to minimize attenuation caused by microbending. An outer secondary coating protects the primary coating against mechanical damage and acts as a barrier to lateral forces. Sometimes a metallic armour layer is added to provide extra protection.

These fiber optic coating layers are applied during the fiber draw, at speeds approaching 100 kilometers per hour (60 mph). Fiber optic coatings are applied using one of two methods: wet-on-dry and wet-on-wet. In wet-on-wet, the fiber passes through a primary coating application, which is then UV cured—then through the secondary coating application, which is subsequently cured. In wet-on-wet, the fiber passes through both the primary and secondary coating applications, then goes to UV curing.

Fiber optic coatings are applied in concentric layers to prevent damage to the fiber during the drawing application and to maximize fiber strength and microbend resistance. Unevenly coated fiber will experience non-uniform forces when the coating expands or contracts, and is susceptible to greater signal attenuation. Under proper drawing and coating processes, the coatings are concentric around the fiber, continuous over the length of the application and have constant thickness.

Fiber optic coatings protect the glass fibers from scratches that could lead to strength degradation. The combination of moisture and scratches accelerates the aging and deterioration of fiber strength. When fiber is subjected to low stresses over a long period, fiber fatigue can occur. Over time or in extreme conditions, these factors combine to cause microscopic flaws in the glass fiber to propagate, which can ultimately result in fiber failure.

Three key characteristics of fiber optic waveguides can be affected by environmental conditions: strength, attenuation and resistance to losses caused by microbending. External fiber optic coatings protect glass optical fiber from environmental conditions that can affect the fiber’s performance and long-term durability. On the inside, coatings ensure the reliability of the signal being carried and help minimize attenuation due to microbending.

Practical issues

Optical fiber cables

An optical fiber cable

Main article: Optical fiber cable

In practical fibers, the cladding is usually coated with a tough resin buffer layer, which may be further surrounded by a jacket layer, usually glass. These layers add strength to the fiber but do not contribute to its optical wave guide properties. Rigid fiber assemblies sometimes put light-absorbing ("dark") glass between the fibers, to prevent light that leaks out of one fiber from entering another. This reduces cross-talk between the fibers, or reduces flare in fiber bundle imaging applications.

Modern cables come in a wide variety of sheathings and armor, designed for applications such as direct burial in trenches, high voltage isolation, dual use as power lines, installation in conduit, lashing to aerial telephone poles, submarine installation, and insertion in paved streets. The cost of small fiber-count pole-mounted cables has greatly decreased due to the high demand for fiber to the home (FTTH) installations in Japan and South Korea.

Fiber cable can be very flexible, but traditional fiber's loss increases greatly if the fiber is bent with a radius smaller than around 30 mm. This creates a problem when the cable is bent around corners or wound around a spool, making FTTX installations more complicated. "Bendable fibers", targeted towards easier installation in home environments, have been standardized as ITU-T G.657. This type of fiber can be bent with a radius as low as 7.5 mm without adverse impact. Even more bendable fibers have been developed. Bendable fiber may also be resistant to fiber hacking, in which the signal in a fiber is surreptitiously monitored by bending the fiber and detecting the leakage.

Another important feature of cable is cable withstanding against the horizontally applied force. It is technically called max tensile strength defining how much force can applied to the cable during the installation period.

Telecom Anatolia fiber optic cable versions are reinforced with aramid yarns or glass yarns as intermediary strength member. In commercial terms, usage of the glass yarns are more cost effective while no loss in mechanical durability of the cable. Glass yarns also protect the cable core against rodents and termites.

Termination and splicing

ST connectors on multi-mode fiber.

Optical fibers are connected to terminal equipment by optical fiber connectors. These connectors are usually of a standard type such as FC, SC, ST, LC, or MTRJ.

Optical fibers may be connected to each other by connectors or by splicing, that is, joining two fibers together to form a continuous optical waveguide. The generally accepted splicing method is arc fusion splicing, which melts the fiber ends together with an electric arc. For quicker fastening jobs, a "mechanical splice" is used.

Fusion splicing is done with a specialized instrument that typically operates as follows: The two cable ends are fastened inside a splice enclosure that will protect the splices, and the fiber ends are stripped of their protective polymer coating (as well as the more sturdy outer jacket, if present). The ends are cleaved (cut) with a precision cleaver to make them perpendicular, and are placed into special holders in the splicer. The splice is usually inspected via a magnified viewing screen to check the cleaves before and after the splice. The splicer uses small motors to align the end faces together, and emits a small spark between electrodes at the gap to burn off dust and moisture. Then the splicer generates a larger spark that raises the temperature above the melting point of the glass, fusing the ends together permanently. The location and energy of the spark is carefully controlled so that the molten core and cladding do not mix, and this minimizes optical loss. A splice loss estimate is measured by the splicer, by directing light through the cladding on one side and measuring the light leaking from the cladding on the other side. A splice loss under 0.1 dB is typical. The complexity of this process makes fiber splicing much more difficult than splicing copper wire.

Mechanical fiber splices are designed to be quicker and easier to install, but there is still the need for stripping, careful cleaning and precision cleaving. The fiber ends are aligned and held together by a precision-made sleeve, often using a clear index-matching gel that enhances the transmission of light across the joint. Such joints typically have higher optical loss and are less robust than fusion splices, especially if the gel is used. All splicing techniques involve installing an enclosure that protects the splice.

Fibers are terminated in connectors that hold the fiber end precisely and securely. A fiber-optic connector is basically a rigid cylindrical barrel surrounded by a sleeve that holds the barrel in its mating socket. The mating mechanism can be push and click, turn and latch (bayonet), or screw-in (threaded). A typical connector is installed by preparing the fiber end and inserting it into the rear of the connector body. Quick-set adhesive is usually used to hold the fiber securely, and a strain relief is secured to the rear. Once the adhesive sets, the fiber's end is polished to a mirror finish. Various polish profiles are used, depending on the type of fiber and the application. For single-mode fiber, fiber ends are typically polished with a slight curvature that makes the mated connectors touch only at their cores. This is called a physical contact (PC) polish. The curved surface may be polished at an angle, to make an angled physical contact" (APC) connection. Such connections have higher loss than PC connections, but greatly reduced back reflection, because light that reflects from the angled surface leaks out of the fiber core. The resulting signal strength loss is called ''gap loss''. APC fiber ends have low back reflection even when disconnected.

In the 1990s, terminating fiber optic cables was labor intensive. The number of parts per connector, polishing of the fibers, and the need to oven-bake the epoxy in each connector made terminating fiber optic cables difficult. Today, many connectors types are on the market that offer easier, less labor intensive ways of terminating cables. Some of the most popular connectors are pre-polished at the factory, and include a gel inside the connector. Those two steps help save money on labor, especially on large projects. A cleave is made at a required length, to get as close to the polished piece already inside the connector. The gel surrounds the point where the two piece meet inside the connector for very little light loss.

Free-space coupling

It is often necessary to align an optical fiber with another optical fiber, or with an optoelectronic device such as a light-emitting diode, a laser diode, or a modulator. This can involve either carefully aligning the fiber and placing it in contact with the device, or can use a lens to allow coupling over an air gap. In some cases the end of the fiber is polished into a curved form that makes it act as a lens.

In a laboratory environment, a bare fiber end is coupled using a fiber launch system, which uses a microscope objective lens to focus the light down to a fine point. A precision translation stage (micro-positioning table) is used to move the lens, fiber, or device to allow the coupling efficiency to be optimized. Fibers with a connector on the end make this process much simpler: the connector is simply plugged into a pre-aligned fiberoptic collimator, which contains a lens that is either accurately positioned with respect to the fiber, or is adjustable. To achieve the best injection efficiency into single-mode fiber, the direction, position, size and divergence of the beam must all be optimized. With good beams, 70 to 90% coupling efficiency can be achieved.

With properly polished single-mode fibers, the emitted beam has an almost perfect Gaussian shape—even in the far field—if a good lens is used. The lens needs to be large enough to support the full numerical aperture of the fiber, and must not introduce aberrations in the beam. Aspheric lenses are typically used.

Fiber fuse

At high optical intensities, above 2 megawatts per square centimeter, when a fiber is subjected to a shock or is otherwise suddenly damaged, a fiber fuse can occur. The reflection from the damage vaporizes the fiber immediately before the break, and this new defect remains reflective so that the damage propagates back toward the transmitter at 1–3 meters per second (4−11 km/h, 2–8 mph). The open fiber control system, which ensures laser eye safety in the event of a broken fiber, can also effectively halt propagation of the fiber fuse. In situations, such as undersea cables, where high power levels might be used without the need for open fiber control, a "fiber fuse" protection device at the transmitter can break the circuit to prevent any damage.

Example

Fiber connections can be used for various types of connections. For example, most high definition televisions offer a digital audio optical connection. This allows the streaming of audio over light, using the TOSLink protocol.

Electric power transmission

Optical fiber can be used to transmit electricity. While the efficiency is not nearly that of traditional copper wire, it is especially useful in situations where it is desirable to not have a metallic conductor as in the case of use near MRI machines, which produce strong magnetic currents.

Preform

Cross-section of a fiber drawn from a D-shaped preform

A preform is a piece of glass used to draw an optical fiber. The preform may consist of several pieces of a glass with different refractive indices, to provide the core and cladding of the fiber. The shape of the preform may be circular, although for some applications such as double-clad fibers another form is preferred. In fiber lasers based on double-clad fiber, an asymmetric shape improves the filling factor for laser pumping.

Due to the surface tension, the shape is smoothed during the drawing process, and the shape of the resulting fiber does not reproduce the sharp edges of the preform. Nevertheless, the careful polishing of the preform is important, any defects of the preform surface affect the optical and mechanical properties of the resulting fiber. In particular, the preform for the test-fiber shown in the figure was not polished well, and the cracks are seen with confocal optical microscope.

See also

• Cable jetting
• Data cable
• Fiber Bragg grating
• Fibre channel
• Fiber pigtail
• Fiber laser
• Gradient-index optics
• Interconnect bottleneck
• Leaky mode
• Light Peak
• Modal bandwidth
• Optical cable
• Optical communication
• Optical fiber connector
• Optical interconnect
• Optical mesh network
• Optical power meter
• Optical time-domain reflectometer
• Optoelectronics
• Parallel optical interface
• Photonic-crystal fiber
• Small form-factor pluggable transceiver
• Soliton, Vector soliton
• Submarine communications cables
• XENPAK

Further reading

• Gambling, W. A., "The Rise and Rise of Optical Fibers", IEEE Journal on Selected Topics in Quantum Electronics, Vol. 6, No. 6, pp. 1084–1093, Nov./Dec. 2000.
• Hecht, Jeff, Understanding Fiber Optics, 4th ed., Prentice-Hall, Upper Saddle River, NJ, USA 2002 (ISBN 0-13-027828-9).
• Mirabito, Michael M.A; and Morgenstern, Barbara L., The New Communications Technologies: Applications, Policy, and Impact, 5th. Edition. Focal Press, 2004. (ISBN 0-24-080586-0).
• Nagel S. R., MacChesney J. B., Walker K. L., "An Overview of the Modified Chemical Vapor Deposition (MCVD) Process and Performance", IEEE Journal of Quantum Electronics, Vol. QE-18, No. 4, p. 459, April 1982.
• Ramaswami, R., Sivarajan, K. N., Optical Networks: A Practical Perspective, Morgan Kaufmann Publishers, San Francisco, 1998 (ISBN 1-55860-445-6).
• VDV Works LLC Lennie Lightwave's Guide To Fiber Optics, http://www.vdvworks.com/LennieLw/ © 2002-6.
• Friedman, Thomas L. (2007). The World is Flat. Picador. ISBN 978-0312425074. The book discusses how fiberoptics has contributed to globalization, and has revolutionized communications, business, and even the distribution of capital among countries.

External links

• The Fiber Optic Association
• FOA color code for connectors
• Lennie Lightwave's Guide To Fiber Optics
• "Fibers", article in RP Photonics' Encyclopedia of Laser Physics and Technology
• How Fiber Optics are made In video
• "Fibre optic technologies", Mercury Communications Ltd, August 1992.
• "Photonics & the future of fibre", Mercury Communications Ltd, March 1993.
• "Fiber Optic Tutorial" Educational site from Arc Electronics
• "Plastic Optical Fiber", Technologies and competitive advantages of POF - Plastic Optical Fiber